2023.1.9 闲话

美好的摆烂生活要结束力（悲

随便推个歌：Fire◎Flower

以下是凑数博 .

---

免责声明：以下内容均为口胡 .

目录

• 定义
  • 幂级数与卷积
  • 在线算法
• 在线卷积
  • 半在线卷积
  • （全）在线卷积
  • \(\Theta(\frac{n\log^2n}{\log\log n})\) 半在线卷积
  • 一些应用实例
• 多元幂级数 / 高维多项式情形
• 「分治 NTT」
  • 求若干次数和一定的多项式之积
  • 求若干次数和一定的有理分式之和
  • 求前缀积之和
• Reference

定义

基础定义就不说了 .

幂级数与卷积

记随便一个交换环为 \(\mathbb A\) .

定义卷积下标系统为一个集合 \(I\) 和其上的运算 \(\circ\) 组成的二元组 \((I,\circ)\)，满足：

• 结合律：\(\forall i,j,k\in I, (i\circ j)\circ k=i\circ(j\circ k)\) .
• 交换律：\(\forall i,j\in I, i\circ j=j\circ i\) .
• 单位元，存在 \(1\in I\) 使得 \(\forall i\in I, 1\circ i=i\) .
• 零元：存在 \(0\in I\) 使得 \(\forall i\in I, 0\circ i=0\) .
• 后效律：对于 \(\forall i\in I\setminus\{0\}\)，对于任意 \(k\in\N_+,j_{1\dots k}\in I\setminus\{0,1\}\)，有 \(i\circ j_1\circ\cdots\circ j_k\neq i\) .

以后默认 \(I\) 表示 \((I,\circ)\)，一般 \(I\) 是有限集，存在歧义时零元和单位元记做 \(0_I,1_I\) .

对于以卷积下标系统 \(I\) 作为下标的序列 \(\{f_i\in\mathbb A\}_{i\in I\setminus\{0\}}\)，定义其生成函数 \(\displaystyle F(z)=\sum_{i\in I}f_iz^i\)，其中 \(z\) 被称为「未定元」，满足：

• \(\forall a\in\mathbb A,i\in I, az^i=z^ia\) .
• \(\forall i,j\in I,z^i\cdot z^j=z^{i\circ j}\) .
• \(z^{0_I}=0_{\mathbb A}\)（消去律）.
• \(z^{1_I}=1_{\mathbb A}\) .

生成函数环记做 \(\mathfrak G[z]\) .

令 \(I=\Z\cap[0,n]\cup\{0_I\}\)，且对于 \(i,j\in I\setminus\{0_I\}\)，定义

\[i\circ j=\begin{cases}i+j&i+j\le n\\0_I&\text{otherwise.}\end{cases} \]

则定义在 \((I,\circ)\) 上的生成函数即为计算时取的普通生成函数（OGF）.

（其实也就是 \(\bmod x^{n+1}\)）

对于 \(1\le j\le k\)，令 \(\mathfrak G_j[x_j]\) 是定义在 \(I_j=\Z\cap[0,n_j-1]\cup\{0_{I_j}\}\) 上的普通生成函数环，其未定元为 \(z_j\)，则 \(\mathfrak G_1[z_1]\times\mathfrak G_2[z_2]\times\cdots\times\mathfrak G_k[z_k]\) 是 \(k\) 元普通生成函数环，可以记做 \(\mathbb A[z_1^{n_1},z_2^{n_2},\cdots,a_k^{n_k}]/(z_1^{n_1},z_2^{n_2},\cdots,z_k^{n_k})\)

对于以卷积下标系统 \(I\) 为下标，\(\mathbb A\) 为系数的序列 \(a,b\)，定义其卷积 \(c=a*b\) 满足：

\[c_k=\sum_{i\circ j=k}a_ib_j \]

熟知环 \(\mathbb F_m\) 上的卷积可以被 \(\Theta(n\log n)\) 次运算计算，后记 \(\mathsf M(n)\) 为多项式乘法的复杂度 .

在线算法

定义 \(I\) 上的序关系 \(\preceq\) 若满足 \(i\preceq j\) 当且仅当 \(\exists k\in I,i\circ k=j\) 则被称为后效序 .

可以发现 \(I\) 上的后效序构成偏序，且最小元为 \(1\)，最大元为 \(0\) .

定义变换 \(\Psi:\underset{n\text{ 个}}{\underbrace{A^{I\setminus \{0\}}\times A^{I\setminus \{0\}}\times\cdots\times A^{I\setminus \{0\}}}}\to A^{I\setminus \{0\}}\) 是后效的当且仅当 \(\forall i\in I\setminus\{0\}\)，令 \(J=\{j\mid j\preceq i\}\)，任取 \(a^{(1)},a^{(2)},\cdots,a^{(n)}\)，记 \(\psi=\Psi[a^{(1)},a{(2)},c\dots,a^{(n)}]\)，则改变任一元素在 \(I\setminus J\) 中的取值，\(\psi_i\) 均不变 .

由此定义后效变换，则可以发现卷积变换是后效的，同样也可以得到左复合 \(f\circ g\) 关于 \(g\) 是后效的 .

下面定义在线算法：

对于一具有 \(n\) 个输入的后效变换 \(\Psi\) 以及一个保后效序的优先级 \(\delta:I\setminus\{0\}\to\N_+\)，满足 \(i\prec j\Rightarrow\delta(i)\prec\delta(j)\) . 称一个算法是在线计算 \(\Psi\) 的当且仅当它能配合黑盒完成如下过程：

1. 令 \(a^{(1)},a^{(2)},\cdots,a^{(n)}\) 均为 \(0\) .
2. 将 \(k\) 从 \(0\) 循环到最大的 \(\delta\) 值，令 \(J_k=\{j\mid\delta(j)=k\}\)，此时 \(\psi^{(k)}=\Psi[a^{(1)},a^{(2)},\cdots,a^{(n)}]\)，对于所有 \(j\in J_k\)，将 \(\psi_j^{(k)}\) 汇报给黑盒 . 汇报结束后，黑盒对于所有 \(i\in[1,n]\cap\mathbb Z\)，\(j\in J_k\) 将 \(a_j^{(i)}\) 赋值 .

在线算法的定义如上 .

在线卷积

以下大概讨论的是 \((\mathbb N_+,+)\) 卷积 .

半在线卷积

半在线卷积：计算卷积 \(c=a*b\) 中，只关于 \(b\) 在线的算法 .

一个例子：

Common Semi-relaxed multiplication

给定序列 \(\{g_n\}\)，\(\{f_n\}\) 由如下递推表述：

\[f_n = c_n \times \sum_{i=0}^{n}f_ig_{n-i} \]

求序列 \(\{f_n\}\) .

将 \(\{f\}\) CDQ 分治（按中点分治），假设处理到了区间 \([l,r]\)，其中 \([l,mid]\) 已经算完，\((mid,r]\) 还没算，则只需处理 \(f_{l\dots mid},g_{mid+1\dots r}\) 对 \(f_{mid+1\dots r}\) 的贡献 .

这个一次卷积即可，或者可以用循环卷积优化常数 .

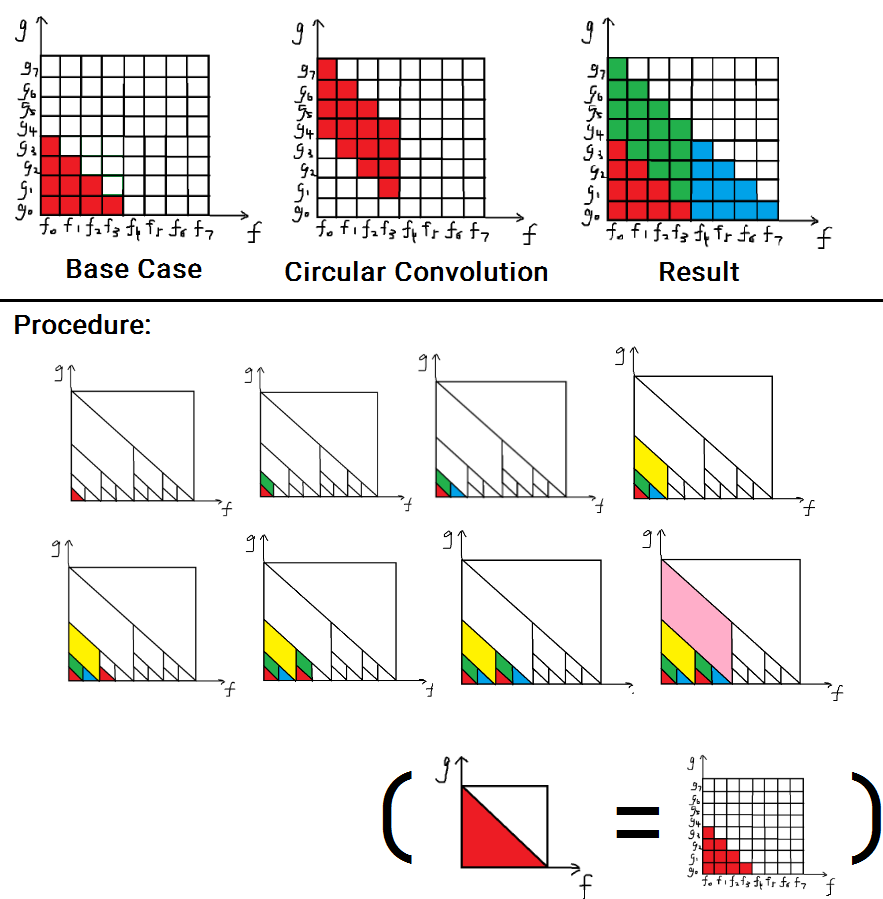
（图源：大部分内容来自 hly1204）

别的半在线卷积大概也是这样，考虑左边对右边的贡献即可做到 \(\Theta(\mathsf M(n)\log n)\) .

注：现在最好的半在线卷积复杂度是 \(\displaystyle O(n\log n\mathrm e^{2\sqrt{\log 2\log\log n}})\)，可以看成单 log 了（upd. 被优化了一些，不改这里了 .

将长度为 \(n\) 的半在线卷积的时间复杂度记做 \(\mathsf S(n)\) .

（全）在线卷积

在线卷积：计算卷积 \(c=a*b\) 中，关于 \(a,b\) 均在线的算法 .

可以得到在线卷积和半在线卷积等难，令在线卷积的时间复杂度 \(\mathsf R(n)\)，则这意味着 \(\mathsf R(n)=\Theta(\mathsf S(n))\) .

半在线卷积显然不强于在线卷积，下面证明在线卷积不强于半在线卷积，也就是将在线卷积归约到半在线卷积 .

考虑倍增解决，过程如下：

1. 令 \(m=\left\lfloor\dfrac n2\right\rfloor\)，则先处理 \(1\dots m\) 的在线卷积 .
2. 对于剩下的部分，考虑对于 \(k>m\) 的卷积式 \(\displaystyle c_k=\sum_{i+j=k}a_ib_j\)，则可以分为如下三部分贡献：
   • \(i,j\le m\)，就是卷积，可以 \(\mathsf M(m)\) 算 .
   • \(i\le m,j>m\)，就是 \(a_{0\dots m}\) 和 \(b_{m+1\dots n}\) 的半在线卷积，可以 \(\mathsf S(m)\) 算 .
   • \(i>m,j\le m\)，就是 \(a_{m+1\dots n}\) 和 \(b_{0\dots m}\) 的半在线卷积，可以 \(\mathsf S(m)\) 算 .

这样就可以得到时间复杂度为 \(T(n)=T(n/2)+\Theta(\mathsf S(n))\) 的算法，根据主定理可以解得 \(T(n)=\Theta(\mathsf S(n))\) .

于是即可得到 \(\mathsf R(n)=\Theta(\mathsf S(n))\) .

大概过程如下：

实际上对角线以下的是在线卷积要求的东西，对角线以上的是一次朴素离线卷积完成的补全正方形来使得可以继续倍增，于是这个玩意看起来不是很能分割子问题但实际上是能分割的（我在写啥

\(\Theta(\frac{n\log^2n}{\log\log n})\) 半在线卷积

考虑把朴素半在线卷积改成 \(k\) 叉分治 .

就是分 \(k\) 叉之后可以把每个子树的点值存一下就可以不用很多 DFT，时间复杂度 \(\displaystyle T(n)=k\cdot T\left(\dfrac nk\right)+\Theta\left(nk+n\log\dfrac nk\right)\) .

这个东西比较神奇我也没整出来到底怎么搞的，反正记一下结论是 \(k=\Theta(\log n)\) 最优，于是时间复杂度是 \(\Theta\left(\dfrac{n\log^2n}{\log\log n}\right)\) .

一些应用实例

Exp

给出形式幂级数 \(f(z)\) 满足 \(f(0)=0\)，求 \(\displaystyle\exp(f(z))=\sum_{i\ge 0}\dfrac{f^i}{i!}\) 的前 \(n\) 项系数 .

注意到 \(\exp(f(z))'=\exp(f(z))\cdot f'(z)\)，于是相当于一个半在线卷积，\(f\) 的系数离线给出，而 \(\exp(f(z))\) 的第 \(i\) 项系数得出后即可算出第 \(i+1\) 项系数，相当于在线给出 .

或者用模板题的形式写出就是两边提取系数得到

\[g_n = \frac{1}{n} \sum_{i=1}^n i f_ig_{n-i} \]

其中 \(f_i\) 是 \(f\) 的第 \(i\) 项系数，\(g_i\) 是 \(\exp(f)\) 的第 \(i\) 项系数 .

2 Conv

给出序列 \(\{g_n\}\)，如下构造 \(\{f_n\}\)：

• \(f_0=1\) .
• \(\displaystyle f_n=\sum_{i=1}^nf^2_ig_{n-i}\) .

求序列 \(\{f\}\) .

半在线卷积时已知 \(f\) 得 \(f^2\) 可以再开一个半在线卷积并行计算 .

下面放一个不给出做法的题 .

XORSHIFT

对于形式幂级数 \(f(z)\) 有一个神奇的运算叫做 XORSHIFT，记做 \(\mathcal X(f(z))\) .

给定 \(n,c\)，求一个形式幂级数使得 \(f(z)\equiv\mathcal X(f(z))\cdot f(z)+c\cdot z\pmod{998244353}\) .

多元幂级数 / 高维多项式情形

EI 说集合幂级数也能干这些操作，但是我不会集合幂级数于是不写 .

对于多元幂级数 \(\mathbb A[z_1^{n_1},z_2^{n_2},\cdots,a_k^{n_k}]/(z_1^{n_1},z_2^{n_2},\cdots,z_k^{n_k})\)，后记 \(\displaystyle n=\sum_{i=1}^kn_i\) .

其实挺凑数的，多元幂级数卷积可以直接看 EI 的解法，link .

这个结果的时间复杂度是 \(\Theta(k\mathsf M(n))\) 的，还是很优的 .

在线卷积就可以按 \(\chi\) 顺序算，这样在线卷积甚至可以 \(\Theta(k\mathsf R(n))\) .

半在线卷积不太好定义，反正弱于在线卷积就对了 .

「分治 NTT」

具体可以看 Alpha1022《社论「不 CDQ 的分治 NTT」(详细揭秘)》.

只放了几个看起来板子比较简单的（

Alpha1022 的题目叫「不 CDQ 的分治 NTT」，然而作者比较菜不 cdq 的那部分都没看懂（

求若干次数和一定的多项式之积

对于多项式簇 \(f_{1\dots m}\)，满足 \(\displaystyle\sum_{i=1}^m\deg f_i=\Theta(n)\)，求 \(\displaystyle\prod_{i=1}^mf_i\) .

考虑对于 \(1\dots m\) cdq 分治，每次把两边暴力乘即可 \(\Theta(n\log^2n)\) .

求若干次数和一定的有理分式之和

对于有理分式簇 \(\left(\dfrac{p_i}{q_i}\right)_{i=1\dots m}\)，满足 \(\displaystyle\sum_{i=1}^m\deg p_i=\Theta(n)\)，\(\displaystyle\sum_{i=1}^m\deg q_i=\Theta(n)\)，求 \(\displaystyle\sum_{i=1}^m\dfrac{p_i}{q_i}\) .

一样的，考虑对于 \(1\dots m\) cdq 分治，每次把两边暴力乘即可 \(\Theta(n\log^2n)\) .

证明是上一个的直接推广 .

求前缀积之和

多项式簇 \(f_{1\dots m},g_{1\dots m},fa_{1\dots m}\)，满足 \(\{f\},\{g\},\{a\}\) 的度数和都是 \(\Theta(n)\) 级别，计算

\[\sum_{i=1}^mf_1f_2\cdots f_{i-1}a_ig_{i+1}g_{i+2}\cdots g_n \]

cdq FFT 维护区间 \(f,g\) 的乘积和答案即可 \(\Theta(n\log^2n)\) .

Reference

• EI, Athekatelan《信息学竞赛中的生成函数计算理论框架》
• hly1204《一种简单的在线卷积理解》《（半）在线卷积简介》
• command_block《半在线卷积小记》
• joke3579《闲话 23.1.6》
• Alpha1022《社论「不 CDQ 的分治 NTT」(详细揭秘)》
• qwaszx《半在线卷积》
• skip2004《O(nlog^2/loglogn)的cdq FFT》

顺序是随便排的，不分先后 .