【好题】[SDOI2011] 染色
\(update:2025.06.14\)
写在前面的
调了非常非常久的紫,细节非常非常多,不失为一道非常非常好的树链剖分题目。
由于这道题首先的思路很难去想,同时也会有特别特别多的坑点,所以文章会很长,读者可以借助右边的目录自行跳至相应需要看的位置。
思路
1. 如何确定一个区间有多少个颜色段
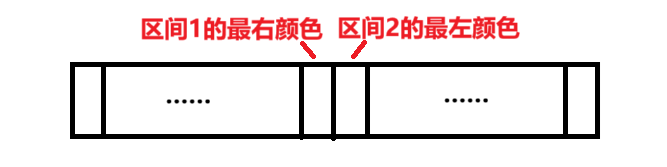
观察上图可以发现,如果左区间的最右颜色和右区间的最左颜色是一样的,那么种数=左区间段数+右区间段数-1;否则就是左右区间段数和。
2. 如何查询颜色段
我们知道树链剖分在查询的时候主要用到的是下面的代码:
inline ll query(int x,int y){
ll ret=0;
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]>=dep[fy]){
ret+=st.query(1,1,n,dfn[fx],dfn[x]);
x=fa[fx];
}
else{
ret+=st.query(1,1,n,dfn[fy],dfn[y]);
y=fa[fy];
}
fx=top[x];
fy=top[y];
}
if(dfn[x]<dfn[y])ret+=st.query(1,1,n,dfn[x],dfn[y]);
else ret+=st.query(1,1,n,dfn[y],dfn[x]);
return ret;
}
它的实现方法是将 \(x\) 节点和 \(y\) 节点分别往上跳,直到两节点链顶相同为止。
很明显的,我们不能直接统计段数了,我们应该把 \(x\) 节点和 \(y\) 节点路径上的颜色段分别记录下来。具体看下面这幅图:
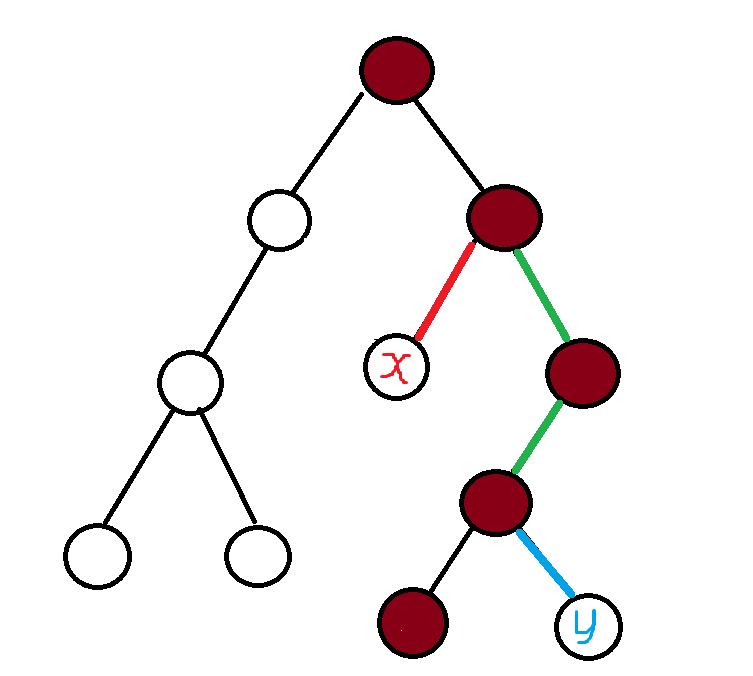
这幅图中,棕色代表一条重链,那么节点 \(x\) 和节点 \(y\) 往上跳的路径分别是 \(\color{red}红色\) 和 \(\color{blue}蓝色\) 所示,我们将其分别记作 lt,rt。最后一条重链上连接两节点的 \(\color{green}绿色\) 我们记作tmp。
我们只需要把 lt,rt,tmp 合并之后,就可以得到总段数了。
解题细节
1. 合并操作
根据上述的思路,树链剖分需要维护每一个节点的 \(3\) 个参数:lc,rc,s。分别代表该区间左颜色、右颜色、颜色段总数。
在合并操作中一定要注意的一点是:当合并的两个区间内其中有一个区间为空时,需要直接返回另一个区间。至于为什么会有出现空区间,后面会提到。
可以写出如下代码:
struct node{
ll lc,rc,tag;
int s;
bool empty(){return (lc==rc&&rc==-1)&&(s==0);}// 判断区间是否为空
};
inline node merge(node a,node b){
if(a.empty())return b;// 空区间返回
if(b.empty())return a;
node ret;
ret.tag=-1;
ret.lc=a.lc,ret.rc=b.rc;// 更新左右端点颜色
ret.s=a.s+b.s;
if(a.rc==b.lc&&a.rc!=-1)--ret.s;// 判断左区间右颜色和右区间左颜色
return ret;
}
2. 线段树
其实和正常线段树的写法没有太大的区别。
这里讲一下合并操作当中为什么会出现判断空区间的步骤。
不难发现,在线段树的代码中,无论是modify函数还是query函数,都难以避免地出现下列语句段:
if(L<=mid) ...;
if(mid<R) ...;
这里就直接去掉了不包含修改区间的区间。
因此,在合并左右节点的时候就可能出现空区间,导致合并不了。
// SGT
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
struct SGT{
ll data[N];
node tree[N<<2];
inline void pushup(int p){
tree[p]=merge(tree[ls(p)],tree[rs(p)]);
}
void build(int p,int pl,int pr){
tree[p].tag=-1;
if(pl==pr){
tree[p].lc=tree[p].rc=data[pl];
tree[p].s=1;
return ;
}
int mid=pl+(pr-pl>>1);
build(ls(p),pl,mid);
build(rs(p),mid+1,pr);
pushup(p);
}
inline void addtag(int p,ll k){
tree[p].lc=tree[p].rc=k;
tree[p].s=1;
tree[p].tag=k;
}
inline void pushdown(int p){
if(tree[p].tag!=-1){
addtag(ls(p),tree[p].tag);
addtag(rs(p),tree[p].tag);
tree[p].tag=-1;
}
}
void modify(int p,int pl,int pr,int L,int R,ll k){
if(L<=pl&&pr<=R){
addtag(p,k);
return ;
}
pushdown(p);
int mid=pl+(pr-pl>>1);
if(L<=mid)modify(ls(p),pl,mid,L,R,k);
if(mid<R)modify(rs(p),mid+1,pr,L,R,k);
pushup(p);
}
node query(int p,int pl,int pr,int L,int R){
if(L<=pl&&pr<=R){
return tree[p];
}
pushdown(p);
int mid=pl+(pr-pl>>1);
node lt={-1,-1,-1,0},rt={-1,-1,-1,0};
if(L<=mid)lt=query(ls(p),pl,mid,L,R);
if(mid<R)rt=query(rs(p),mid+1,pr,L,R);
return merge(lt,rt);
}
}st;
3. 树链剖分-查询
在思路中,重中之重的是查询操作。
我们用xt记录节点 \(x\) 在向上跳的时候的区间信息;同理,用yt记录节点 \(y\) 的;用tmp记录本次跳动所查询到的东西。
那么,问题来了。在跳动过程中,究竟是merge(xt,tmp)还是merge(tmp,xt)呢?我们看一个图就知道了。
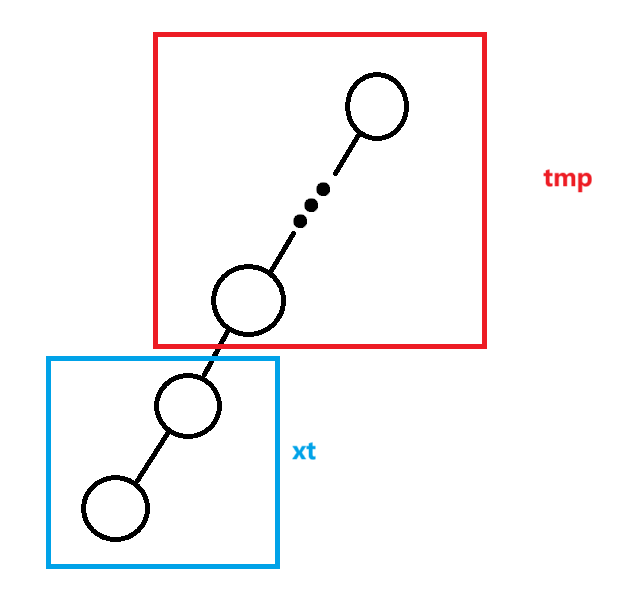
在上图这棵树当中,很明显的xt的深度要比tmp的深度要大,因此合并的时候,优先应该是深度小的为合并左区间。应该是merge(tmp,xt)。
最后就是如何处理连接xt和yt的链的问题了。

仍然用回上面这幅图。当我们要进行merge(xt,tmp)的时候,xt应该是调转过来去合并的。所以要将xt翻转过来,也就是将xt.lc和xt.rc交换。yt同理。根据上述思路,可以写出查询代码。
inline node query(int x,int y){
int fx=top[x],fy=top[y];
node xt={-1,-1,-1,0},yt={-1,-1,-1,0},tmp;
while(fx!=fy){
if(dep[fx]>=dep[fy]){
tmp=st.query(1,1,n,dfn[fx],dfn[x]);
xt=merge(tmp,xt);
x=fa[fx];
}else{
tmp=st.query(1,1,n,dfn[fy],dfn[y]);
yt=merge(tmp,yt);
y=fa[fy];
}
fx=top[x];
fy=top[y];
}
if(dfn[x]<=dfn[y]){
tmp=st.query(1,1,n,dfn[x],dfn[y]);
xt.tag=xt.lc;
xt.lc=xt.rc;
xt.rc=xt.tag;
xt.tag=-1;
xt=merge(xt,tmp);
return merge(xt,yt);
}else{
tmp=st.query(1,1,n,dfn[y],dfn[x]);
yt.tag=yt.lc;
yt.lc=yt.rc;
yt.rc=yt.tag;
yt.tag=-1;
yt=merge(yt,tmp);
return merge(yt,xt);
}
}
4. 树链剖分-修改
和树链剖分的查询操作没有什么差别。都是往上跳,然后一直修改,这里直接给出代码理解即可。
inline void modify(int x,int y,ll k){
int fx=top[x],fy=top[y];
while(fx!=fy){
if(dep[fx]>=dep[fy]){
st.modify(1,1,n,dfn[fx],dfn[x],k);
x=fa[fx];
}else{
st.modify(1,1,n,dfn[fy],dfn[y],k);
y=fa[fy];
}
fx=top[x];
fy=top[y];
}
if(dfn[x]<=dfn[y]){
st.modify(1,1,n,dfn[x],dfn[y],k);
}else
st.modify(1,1,n,dfn[y],dfn[x],k);
return ;
}
总结+小提醒
这道题是一道十分不错的树链剖分思维+练手题目。可以大大增强对树链剖分的应用和掌握。不要随随便便抄题解。
如果你遇到了RE的问题,我去看了一下洛谷的讨论,建议不要使用
scanf语句。可以改成:inline char readc(){ char ch=getchar_unlocked(); while(ch!='C'&&ch!='Q')ch=getchar_unlocked(); return ch; }
创作不易,给个关注吧!!!谢谢。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号