[冲刺国赛2022] match
一、题目
二、解法
分析错误算法与 \(\tt kmp\) 算法的异同，\(\tt kmp\) 算法在当前字符失配时，会跳到其最长 \(\tt border\) 处，而错误算法在失配时会直接跳到 \(0\)，这说明如果通过跳 \(\tt border\) 完成的匹配，会让错误算法直接寄掉。
由此引出的一个关键的 \(\tt observation\) 是：\(f\) 数组的形式一定是 \(0,1,2...k_1,0,1,2...k_2,0\)，也就是每段非 \(0\) 的 \(f\) 一定是一个公差为 \(1\) 的等差数列，段之间不相交，相邻两段之间间隔至少一个 \(0\)
考虑枚举最长的连续段 \(S[l,r]\)，可以发现它一定是 \(T\) 的一个前缀。此时 \(T\) 合法的条件是：\(S\) 中不存在一个更长的子串是 \(T\) 的前缀；把原串 \(S\) 和子串 \(S[l,r]\) 执行 \(\tt kmp\) 算法时，不存在通过跳 \(\tt border\) 完成的匹配。
这样我们得到了 \(O(n^3)\) 的算法，随便减减枝就可以通过原题数据。当然神 \(\tt OUYE\) 是不满足于此的，我们建出原串的后缀字典树（把每个后缀插入 \(\tt trie\) 中得到的结构），来看看这个树上有什么性质：
考虑按 \(\tt dfs\) 的顺序枚举 \(S[l,r]\)，定义失配串为：，考虑 \(S[l,r]\) 及其前缀在原串中的所有出现位置，记为集合 \(Z\)，存在某个出现位置不被 \(Z\) 中元素包含的，可以通过 \(S[l,r]\) 的一个前缀添加某个字符得到的串。那么 \(T\) 合法的第二个条件可以等价为：所有失配串不存在 \(\tt border\)（因为失配串在原串中作为某个连续段独立出现，如果存在 \(\tt border\) 就可以通过跳 \(\tt border\) 来完成匹配）
定义失配点为失配串在树上对应的节点，那么我们现在的任务是维护所有失配点，并且判断是否存在失配点的 \(\tt border\) 大于 \(0\)，我们在后缀字典树的链上标记出所有的失配点（递归时向失配集合加入兄弟节点）：
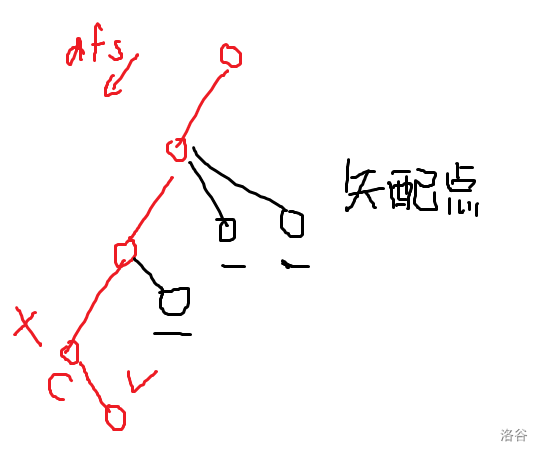
设 \(x\) 的走字符 \(c\) 的儿子是 \(v\)，因为某些失配串可能在 \(x\) 中没出现但是在 \(v\) 中出现了，所以我们要扣除是 \(v\) 后缀一些失配串的出现次数（如果出现次数为 \(0\) 就从失配集合中踢除）
如何找到这些失配串呢？考虑失配点的父亲一定是 \(x\) 的后缀，同时他也一定是 \(x\) 的前缀（这是根据定义来的），这说明失配点的父亲一定是 \(x\) 的 \(\tt border\)；所以我们可以从 \(x\) 一直往上 \(\tt fail\)，设 \(\tt fail\) 到的节点是 \(t\)，拿到点 \(t\) 在 \(c\) 方向的儿子，然后扣除它在 \(v\) 中的出现次数（即 \(cnt_v\)，子串 \(v\) 在原串中的出现次数）
为了不扣重我们需要在链上 \(t\) 的下一个字符是 \(c\) 时停下，因为这部分在先前的递归已经被扣除过了。这样我们就可以方便地维护存在 \(\tt border\)，并且独立出现次数非 \(0\) 的失配串个数。
由于我们在恰当的时机停下了，复杂度基于在后缀字典树上做 \(\tt kmp\) 的复杂度。一共有 \(O(n)\) 条链，可以看成每一条链分别 \(\tt kmp\)，那么一条链的时间是 \(O(n)\) 的，总时间复杂度 \(O(n^2)\)
#include <cstdio>
const int M = 2005;
const int N = M*M;
const int MOD = 998244353;
#define ll long long
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,c[N][5],fa[N],cnt[N],st[N],nx[N];
ll ans,pw[M];char s[M];int nm;
ll qkpow(ll a,ll b)
{
ll r=1;
while(b>0)
{
if(b&1) r=r*a%MOD;
a=a*a%MOD;
b>>=1;
}
return r;
}
void dfs(int u,int ln)
{
//get all fail
for(int i=0;i<5;i++) if(c[u][i])
{
int v=c[u][i],t=fa[u];
while(t && nx[t]!=i) t=fa[t];
if(u && nx[t]==i) fa[v]=c[t][i];
}
//go into v
for(int i=0;i<5;i++) if(c[u][i])
{
int v=c[u][i],t=fa[u];
//delete some suffix of v
while(t && nx[t]!=i)
{
if(c[t][i])
{
int o=c[t][i];
st[o]-=cnt[v];
if(st[o]==0) nm-=(fa[o]>0);
}
t=fa[t];
}
//add the brother of v
for(int j=0;j<5;j++) if(c[u][j] && i!=j)
st[c[u][j]]+=cnt[c[u][j]],nm+=(fa[c[u][j]]>0);
nx[u]=i;dfs(v,ln+1);
for(int j=0;j<5;j++) if(c[u][j] && i!=j)
st[c[u][j]]-=cnt[c[u][j]],nm-=(fa[c[u][j]]>0);
t=fa[u];
while(t && nx[t]!=i)
{
if(c[t][i])
{
int o=c[t][i];
if(st[o]==0) nm+=(fa[o]>0);
st[o]+=cnt[v];
}
t=fa[t];
}
}
int ok=1,cnt=5;
for(int i=0;i<5;i++) if(c[u][i])
ok&=(fa[c[u][i]]==0),cnt--;
if(ok && !nm)
{
if(ln<m) ans=(ans+cnt*pw[m-ln-1])%MOD;
if(ln==m) ans=(ans+1)%MOD;
}
}
signed main()
{
freopen("match.in","r",stdin);
freopen("match.out","w",stdout);
n=read();m=read();scanf("%s",s+1);
for(int i=pw[0]=1;i<=m;i++)
pw[i]=pw[i-1]*5ll%MOD;
for(int i=1;i<=n;i++)
for(int j=i,p=0;j<=n;j++)
{
int w=s[j]-'a';
if(!c[p][w]) c[p][w]=++k;
p=c[p][w];cnt[p]++;
}
dfs(0,0);
printf("%lld\n",ans*qkpow(pw[m],MOD-2)%MOD);
}
