CRYPTOHACK-Elliptic Curves部分wp

CRYPTOHACK-Elliptic Curves

前置知识

一种椭圆曲线的形式

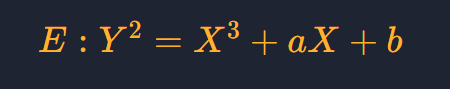
几何表示P+Q=-R，R(x,y)，-R(x,-y)

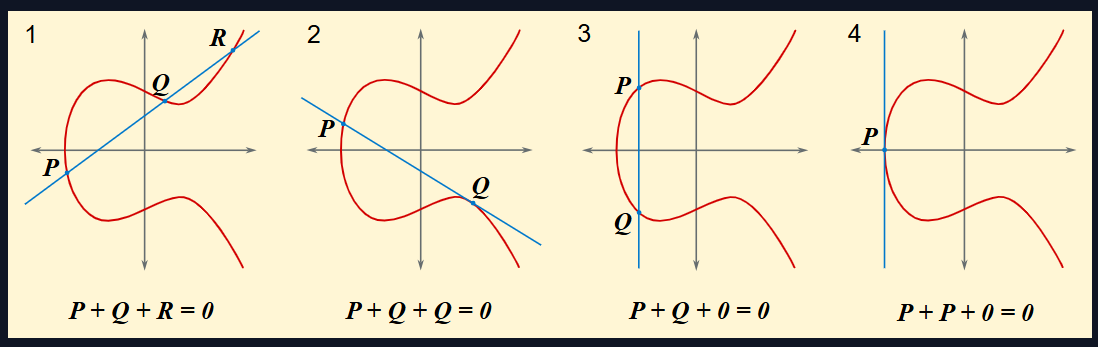
在椭圆曲线密码学中，O 是 无穷远点（point at infinity），它是椭圆曲线加法群的 单位元（identity element）。

几何意义：
在射影几何中，无穷远点 O 可以理解为所有垂直于 x-轴的平行直线的“交点”，它不属于普通的仿射平面 R² 或 F_p²，但存在于射影平面中。
代数意义：
在椭圆曲线的加法群中，O满足：

P+O=O+P=P（对任意点 P）

即它是加法的“零元”。

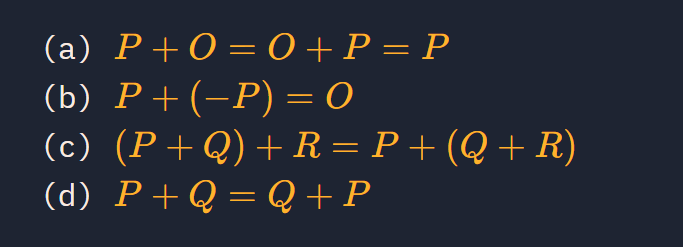
Background Reading

可使用交换律的群：阿贝尔群（Abelian）

Point Negation

注意将负数转换到模p下就行，答案是（8045，-6936%p）

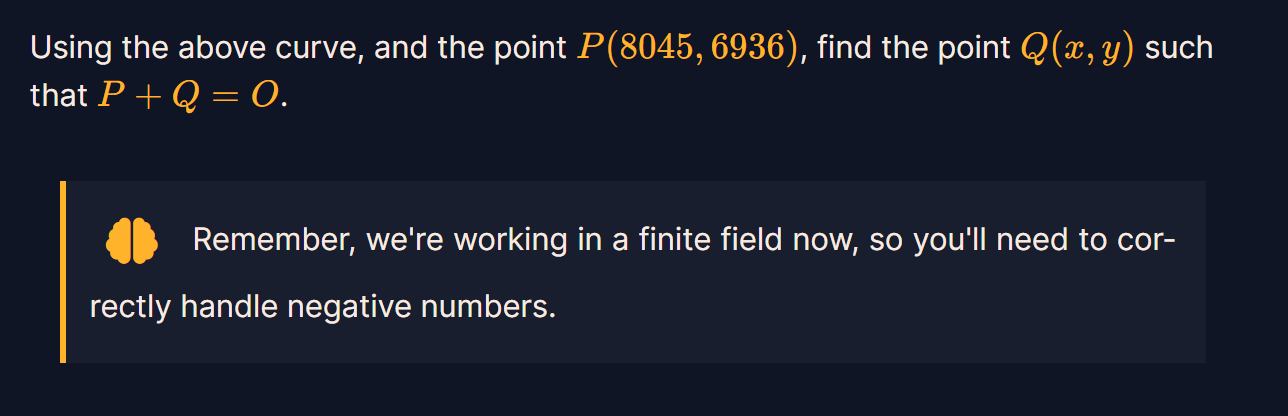
Point Addition

计算点加法算法步骤

证明：把直线方程代入椭圆曲线方程再用韦达定理可得

注意：所有运算在有限域F_p内，除法需计算模p下的逆元

题：

exp：

from gmpy2 import *
def Point_Addition(P,Q):
    if P is None:
        return Q
    if Q is None:
        return P
    x1,y1=P
    x2,y2=Q
    if x1==x2 and (y1+y2)%p==0:
        return None

    if P==Q:
        d=invert(2*y1,p)
        k=(((3*x1*x1+a)%p)*d)%p
    else:
        d=invert(x1 - x2, p)
        k=(((y1-y2)%p)*d)%p
    x3=(k*k-x1-x2)%p
    y3=(k*(x1-x3)-y1)%p
    return (x3,y3)
P=(493,5564)
Q=(1539,4742)
R=(4403,5202)
a=497
p=9739
res1=Point_Addition(P,P)
res2=Point_Addition(res1,Q)
res=Point_Addition(res2,R)
print(res)

Scalar Multiplication

标量乘法算法步骤

题：

exp：

from gmpy2 import *
def Point_Addition(P,Q,a,p):
    if P is None:
        return Q
    if Q is None:
        return P
    x1,y1=P
    x2,y2=Q
    if x1==x2 and (y1+y2)%p==0:
        return None

    if P==Q:
        d=invert(2*y1,p)
        k=(((3*x1*x1+a)%p)*d)%p
    else:
        d=invert(x1 - x2, p)
        k=(((y1-y2)%p)*d)%p
    x3=(k*k-x1-x2)%p
    y3=(k*(x1-x3)-y1)%p
    return (x3,y3)
def Scalar_Multiplication(n,X,a,p):
    Q=X
    R=None
    while n>0:
        if n%2==1:
            R=Point_Addition(R,Q,a,p)
        Q=Point_Addition(Q,Q,a,p)

        n=n//2
    return R
n=7863
p=9739
a=497
X=(2339,2213)
print(Scalar_Multiplication(n,X,a,p))

Curves and Logs

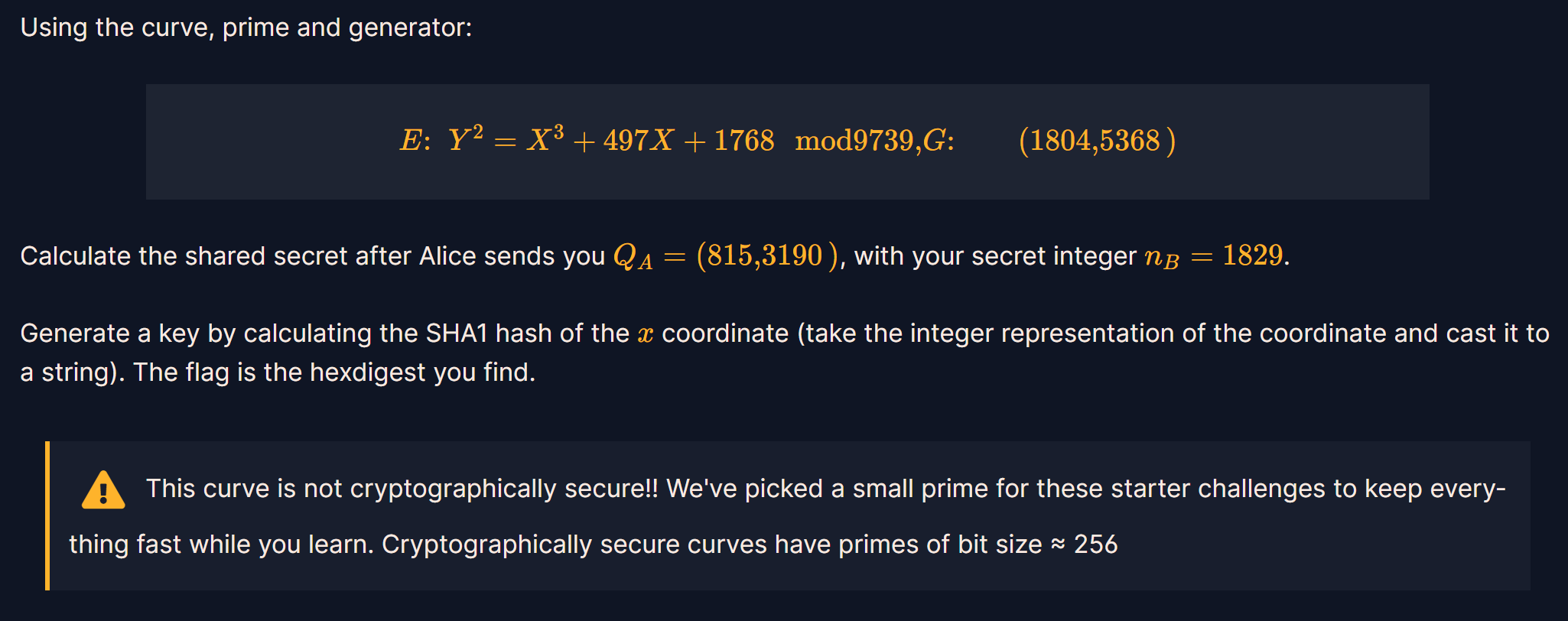
Elliptic Curve Diffie-Hellman密钥交换算法，跟Diffie-Hellman很像，只是套了椭圆曲线的外壳

题：

跟上题一样，只是要计算x坐标的哈希值

exp：

from gmpy2 import *
import hashlib
def Point_Addition(P,Q,a,p):
    if P is None:
        return Q
    if Q is None:
        return P
    x1,y1=P
    x2,y2=Q
    if x1==x2 and (y1+y2)%p==0:
        return None

    if P==Q:
        d=invert(2*y1,p)
        k=(((3*x1*x1+a)%p)*d)%p
    else:
        d=invert(x1 - x2, p)
        k=(((y1-y2)%p)*d)%p
    x3=(k*k-x1-x2)%p
    y3=(k*(x1-x3)-y1)%p
    return (x3,y3)
def Scalar_Multiplication(n,X,a,p):
    Q=X
    R=None
    while n>0:
        if n%2==1:
            R=Point_Addition(R,Q,a,p)
        Q=Point_Addition(Q,Q,a,p)

        n=n//2
    return R
n=1829
p=9739
a=497
X=(815,3190)
print(Scalar_Multiplication(n,X,a,p))#7929
sha1=hashlib.new('sha1')
sha1.update(b'7929')
print(sha1.hexdigest())

Efficient Exchange

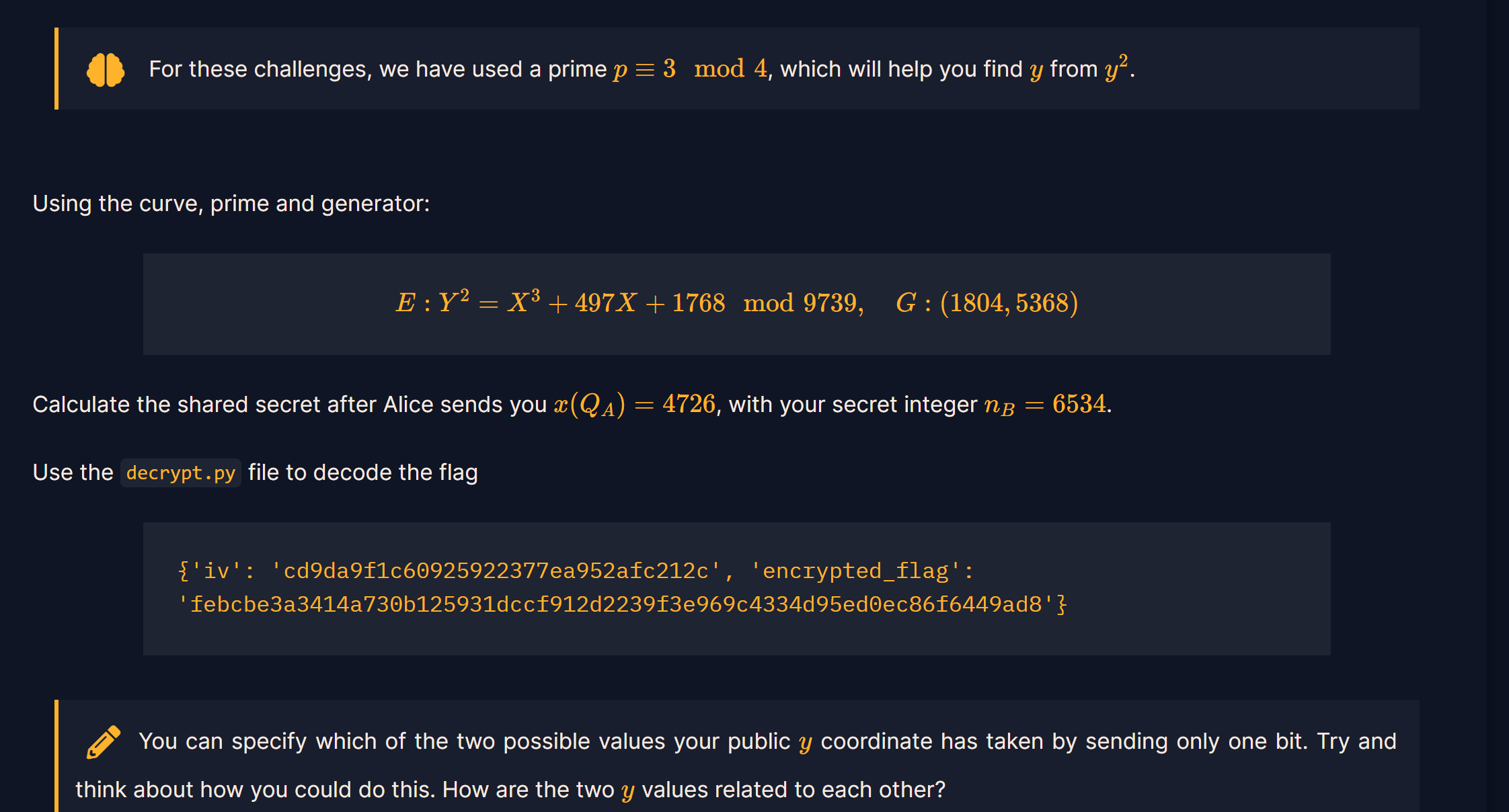
Alice和Bob意识到没必要同时发送公钥Q（仍然在椭圆曲线上）的x，y两个坐标，事实上，相同的x对应两种y的取值，所以只需发送x坐标的值即可还原出y值（用二次剩余中求平方根的知识），对于两个可能的y值，经标量相乘最终得到共享密钥S的x是一样的（关于x轴对称），据此可得最终的共享密钥x

题：

exp：

from gmpy2 import *
import hashlib
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
def Point_Addition(P,Q,a,p):
    if P is None:
        return Q
    if Q is None:
        return P
    x1,y1=P
    x2,y2=Q
    if x1==x2 and (y1+y2)%p==0:
        return None

    if P==Q:
        d=invert(2*y1,p)
        k=(((3*x1*x1+a)%p)*d)%p
    else:
        d=invert(x1 - x2, p)
        k=(((y1-y2)%p)*d)%p
    x3=(k*k-x1-x2)%p
    y3=(k*(x1-x3)-y1)%p
    return (x3,y3)
def Scalar_Multiplication(n,X,a,p):
    Q=X
    R=None
    while n>0:
        if n%2==1:
            R=Point_Addition(R,Q,a,p)
        Q=Point_Addition(Q,Q,a,p)

        n=n//2
    return R
n=6534
p=9739
a=497
x=4726
m=(x*x*x+497*x+1768)%p
y=pow(m,(p+1)//4,p)#还原y(Q)
X=(4726,y)#Q
xx=str(Scalar_Multiplication(n,X,a,p)[0])#共享密钥x(S)

def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Decrypt flag
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = xx
iv = 'cd9da9f1c60925922377ea952afc212c'
ciphertext = 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'

print(decrypt_flag(shared_secret, iv, ciphertext))

Montgomery's Ladder

蒙哥马利二进制算法计算标量乘法[k]P

蒙哥马利曲线

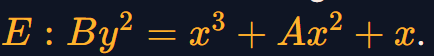
点加运算

倍点运算

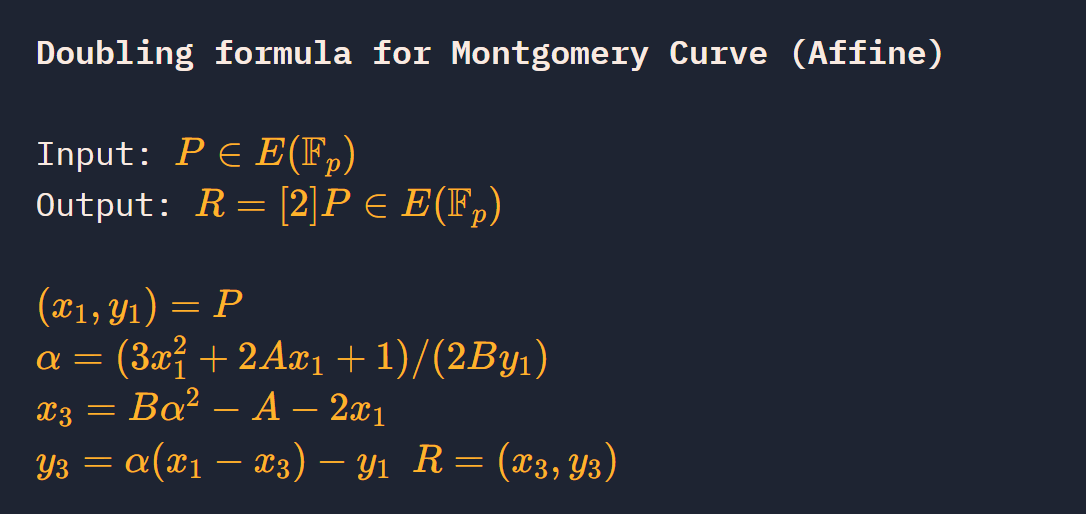
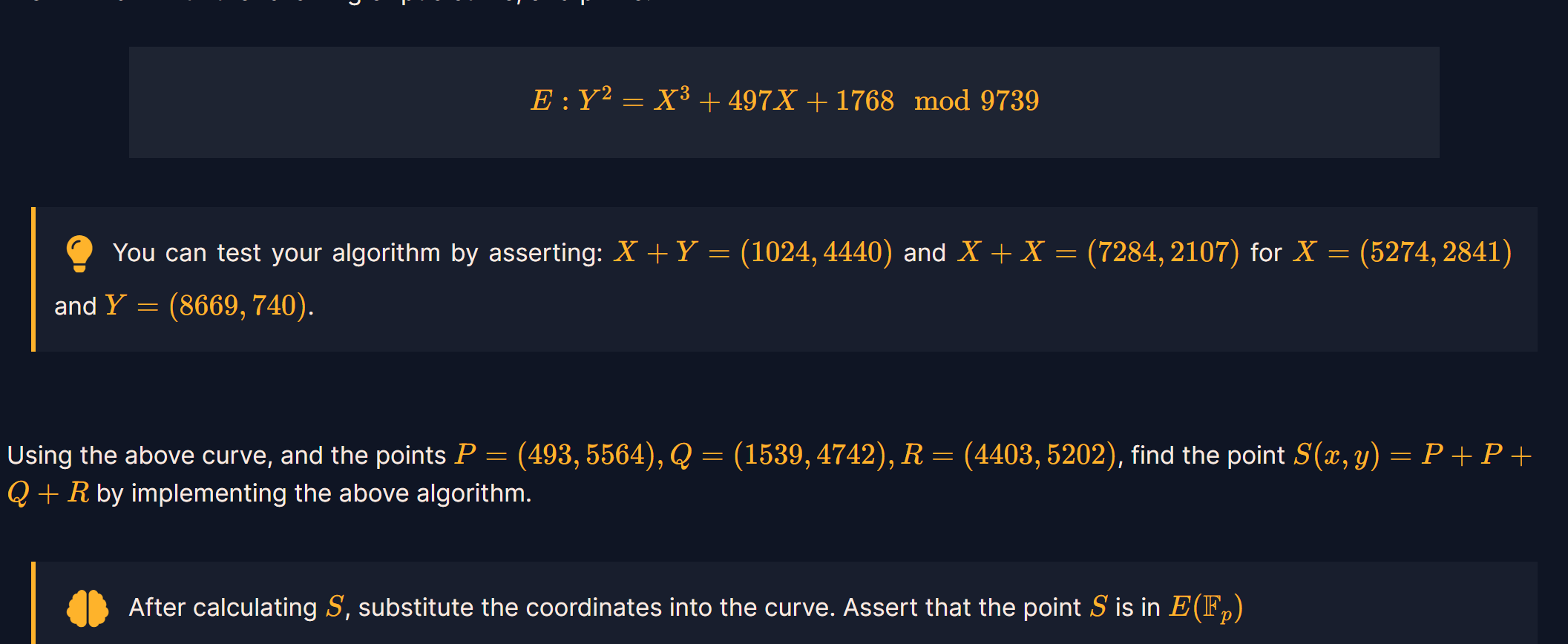
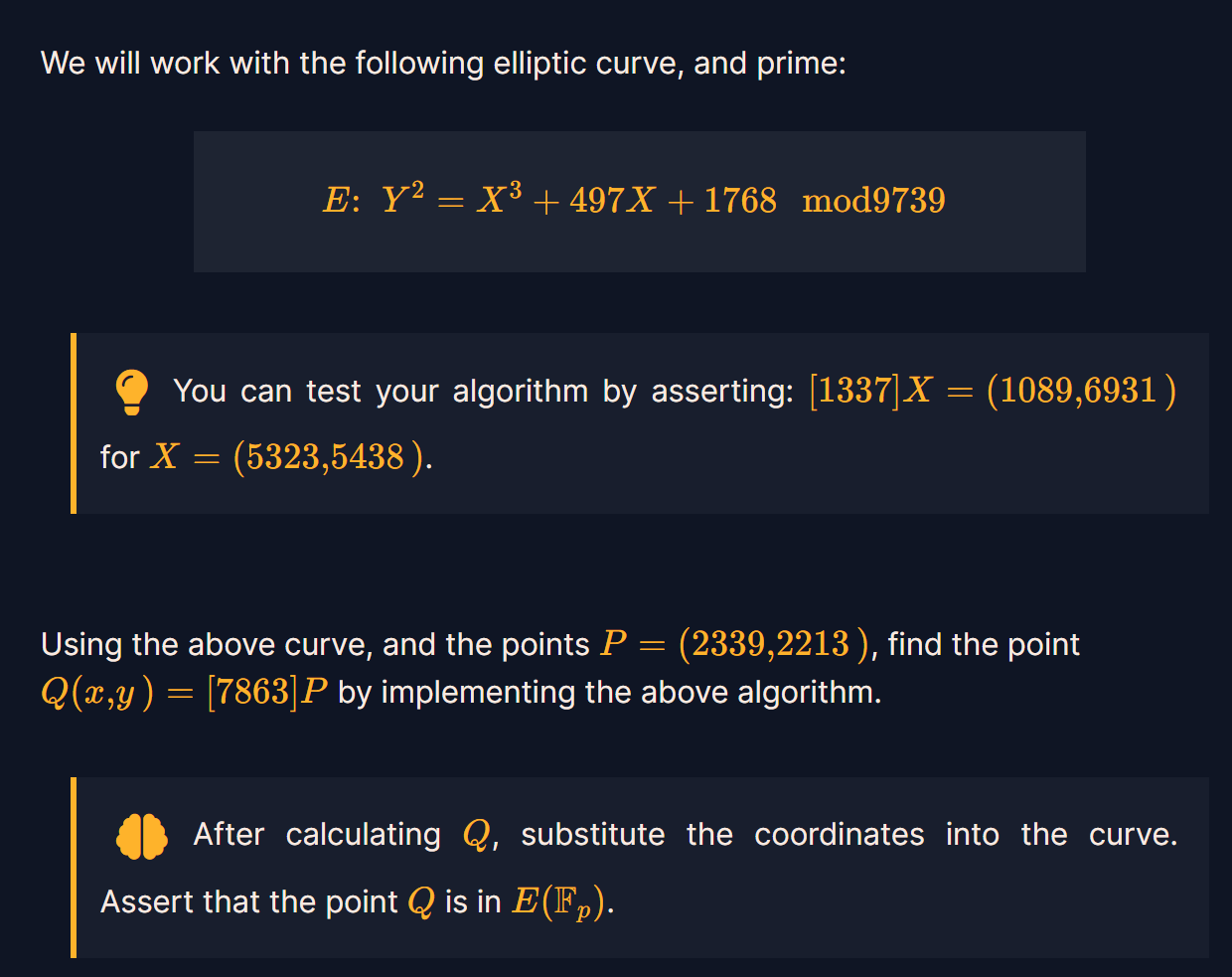
题：求Q的x坐标

exp：

from gmpy2 import *
from sympy import *
def addition(P,Q,p,A,B):#P+Q
    x1,y1=P
    x2,y2=Q
    if P == (0, 0):  # P是无穷远点
        return Q
    if Q == (0, 0):  # Q是无穷远点
        return P
    if x1 == x2:
        if y1 == y2:
            return doubling(P, p, A, B)  # 相同点相加 → 点加倍
        else:
            return (0, 0)  # 相反点相加 → 无穷远点
    else:
        try:
            d=invert(x2-x1,p)
            alpha=(((y2-y1)%p)*d)%p
            x3=(B*alpha*alpha-A-x1-x2)%p
            y3=(alpha*(x1-x3)-y1)%p
            return x3,y3
        except ZeroDivisionError:  # 额外捕获异常
            return (0, 0)
def doubling(P,p,A,B):
    x1, y1 = P
    if y1 == 0:  # 处理y=0的情况
        return (0, 0)
    try:
        d=invert(2*B*y1,p)
        alpha1=(((3*x1*x1+2*A*x1+1)%p)*d)%p
        x3=(B*alpha1*alpha1-A-2*x1)%p
        y3=(alpha1*(x1-x3)-y1)%p
        return x3,y3
    except ZeroDivisionError:
        return (0,0)
def scalar(P,p,A,B,k):
    R0=P
    R1=doubling(P,p,A,B)
    for i in range(k.bit_length()-2,-1,-1):
        if (k>>i)&1:
            R0=addition(R0,R1,p,A,B)
            R1=doubling(R1,p,A,B)
        else:
            R1=addition(R0,R1,p,A,B)
            R0=doubling(R0,p,A,B)#一开始老错，后来发现是这两行顺序搞反了，改变了R0的值去更新R1是

    return R0

n=int("0x1337c0decafe",16)
x=9

p=((2**255)-19)

A=486662
B=1
a=x**3+A*x*x+x
y=sqrt_mod(a,p)
P=(x,y)
res=scalar(P,p,A,B,n)
print(res)

未完待续......

posted @ 2025-05-11 23:14 C0E1 阅读(148) 评论(0) 收藏举报

刷新页面返回顶部

C0E1

CRYPTOHACK-Elliptic Curves部分wp