Diffie-Hellman密钥协商算法

原根

1.定义

（1）阶

（2）设 a 和 m 是互质的整数（即 gcd⁡(a,m)=1）。如果 a 的阶（order）等于 φ(m)（欧拉函数），即：

δ_m(a) = φ(m)

那么 a 称为模 m 的一个原根。

换句话说，a 是模 m 的原根，当且仅当：

但：

a^φ(m) ≡ 1(mod m)

2.性质

1.生成所有剩余类

如果 g 是模 m 的原根，那么：

{g¹,g²,…,g^φ(m)}(mod m)

可以生成所有与 m 互质的剩余类（即乘法群 (Z/mZ)*的所有元素)。

证明：

运用反证法，假设存在i≠j，且 1≤i<j≤φ(m) 使得 gⁱ ≡ g^j (mod m)

那么 g^j−i ≡ 1 (mod m)

由于 0<j−i<φ(m)，这与 g的阶是 φ(m) 矛盾。因此：

g¹,g²,…,g^φ(m) (mod m)

①两两不同余。

②因为gcd(g,m)=1，所以gcd(g^k,m)=1，所以所有元素与m互质

③覆盖所有简化剩余类：{g¹,g²,…,g^φ(m)} 有 φ(m)个不同的元素

3.原根的存在性

• 原根不一定总是存在。
• 当且仅当 m=2,4,p^k或 2p^k（其中 p 是奇素数，k≥1）时，模 m才有原根。

离散对数

离散对数 - OI Wiki

1.定义

2.性质

Diffie-Hellman密钥协商算法

Diffie-Hellman密钥协商算法 - Qcer - 博客园

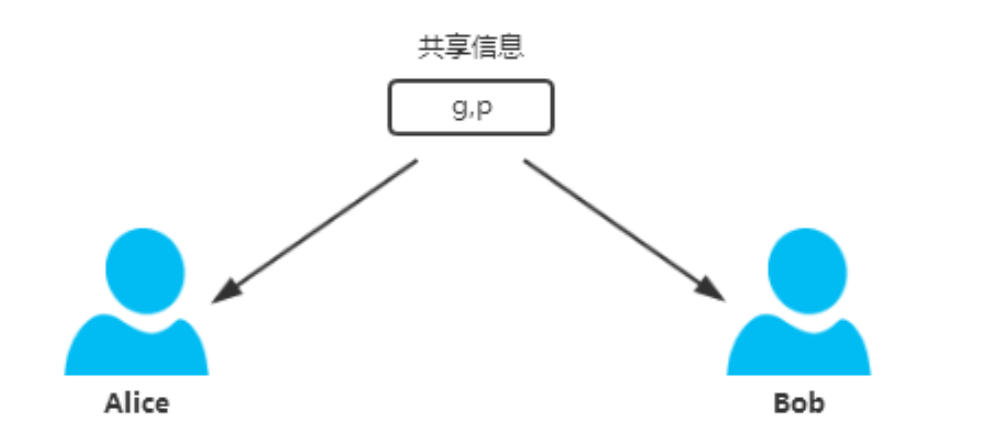
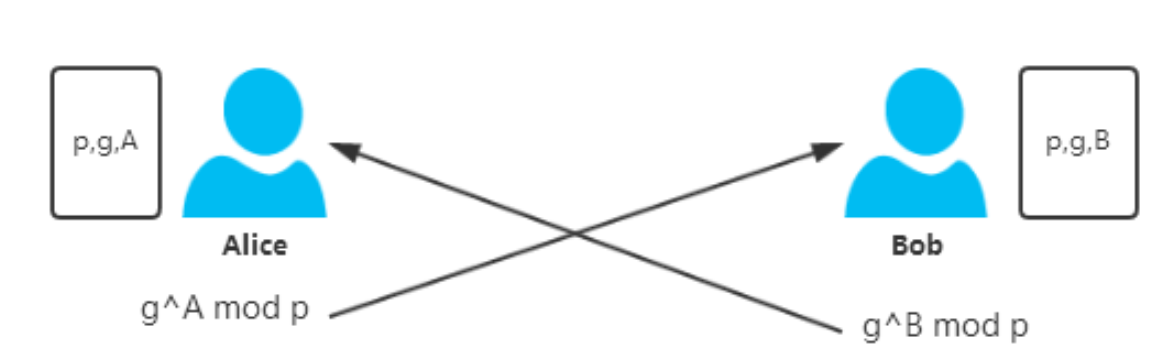
协商密钥：K_a = Y_b^A (mod p)，K_b = Y_a^B (mod p)，

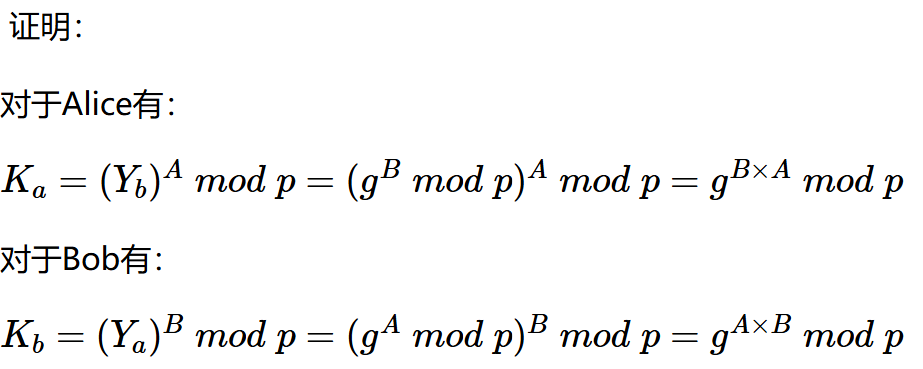
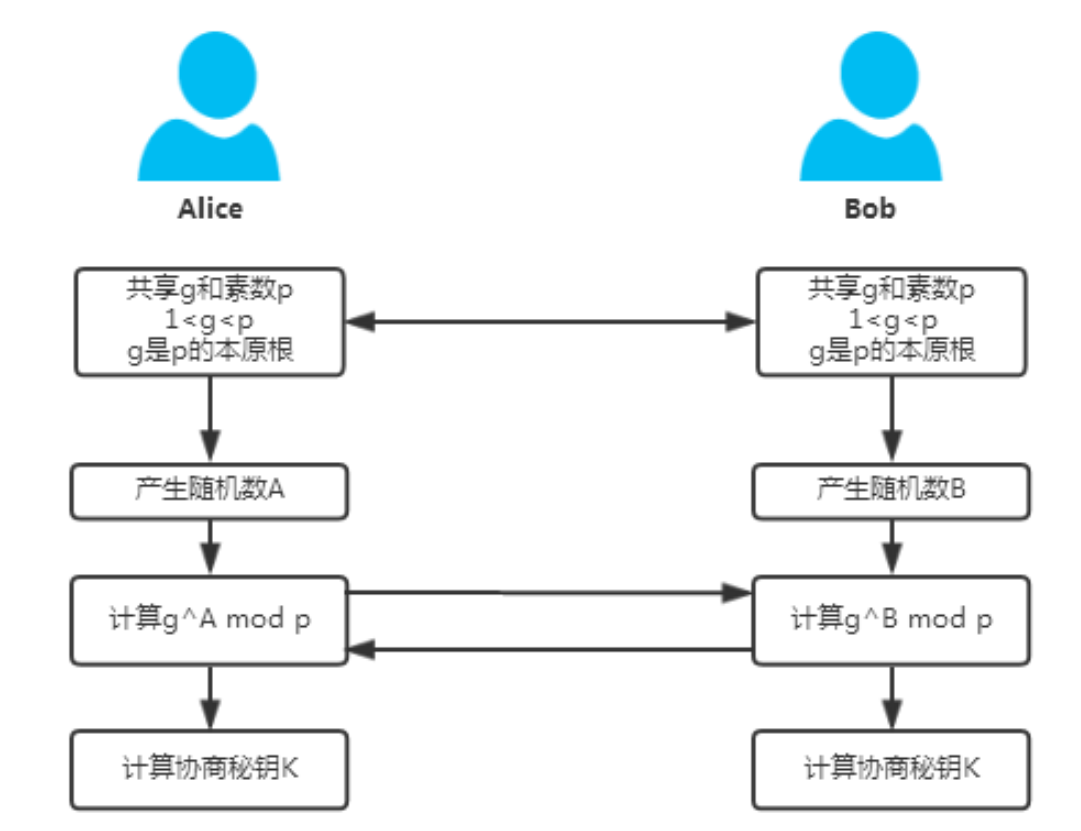
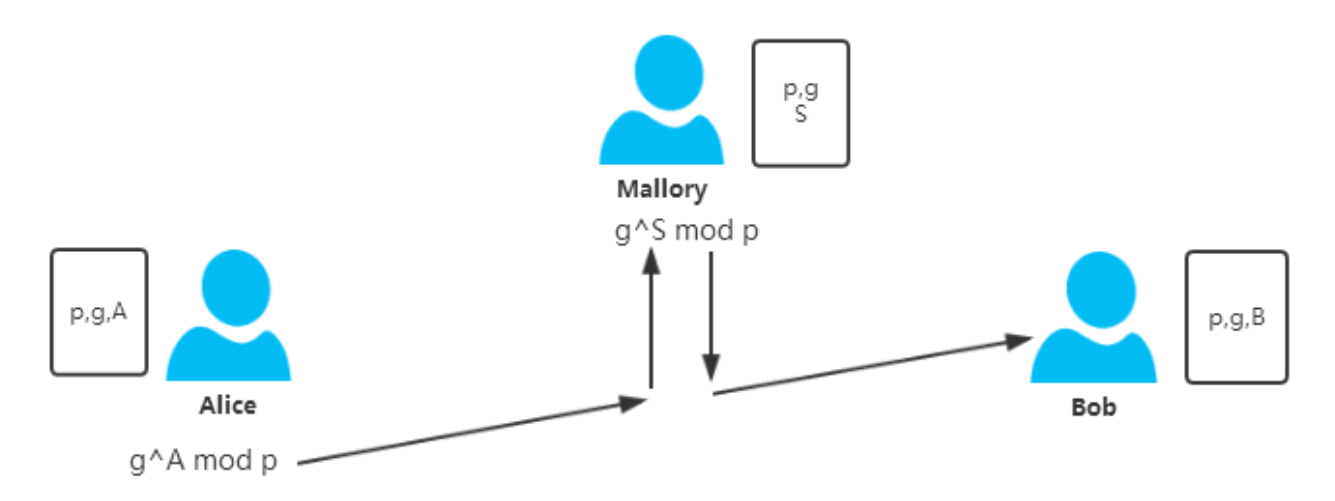
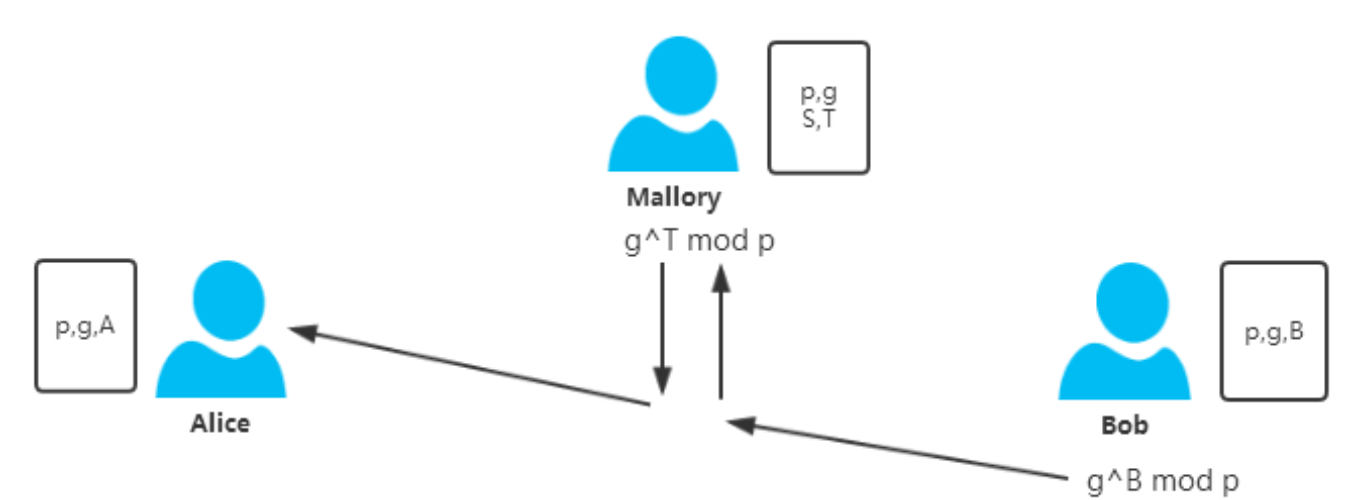
中间主动攻击者Mallory