Franklin-Reiter相关消息攻击和RSA的一种题型

Franklin-Reiter相关消息攻击

关于Franklin-Reiter相关消息攻击的知识这篇文章写的很具体

关于我想了一段时间才弄懂的点做一个解释

（x-M₂)是两个多项式的共同因子（因式分解）

from flag import FLAG
from Crypto.Util.number import getPrime, bytes_to_long
import hashlib

def generate_key(bits=512):
    p = getPrime(bits)
    q = getPrime(bits)
    return p * q, 3


def hash(x):
    return int(hashlib.md5(str(x).encode()).hexdigest(), 16)


def encrypt(m, n, e):
    x1, x2 = 307, 7
    c1 = pow(m + hash(x1), e, n)
    c2 = pow(m + hash(x2), e, n)
    return c1, c2


m = bytes_to_long(FLAG)
n, e = generate_key()
c1, c2 = encrypt(m, n, e)
print(f"n = {n}")
print(f"e = {e}")
print(f"c1 = {c1}")
print(f"c2 = {c2}")

exp：sagemath环境下

import hashlib
n=100885785256342169056765112203447042910886647238787490462506364977429519290706204521984596783537199842140535823208433284571495132415960381175163434675775328905396713032321690195499705998621049971024487732085874710868565606249892231863632731481840542506411757024315315311788336796336407286355303887021285839839
e = 3
c1=41973910895747673899187679417443865074160589754180118442365040608786257167532976519645413349472355652086604920132172274308809002827286937134629295632868623764934042989648498006706284984313078230848738989331579140105876643369041029438708179499450424414752031366276378743595588425043730563346092854896545408366
c2=41973912583926901518444642835111314526720967879172223986535984124576403651553273447618087600591347032422378272332279802860926604693828116337548053006928860031338938935746179912330961194768693506712533420818446672613053888256943921222915644107389736912059397747390472331492265060448066180414639931364582445814
x1, x2 = 307, 7

def hash(x):
    return int(hashlib.md5(str(x).encode()).hexdigest(), 16)

X1 = hash(x1)
X2 = hash(x2)
delta = X2 - X1

# 定义多项式环
R.<x> = PolynomialRing(Zmod(n))  
f = x^e - c1
g = (x + delta)^e - c2

# 计算 GCD（使用扩展欧几里得算法）
def poly_gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a.monic()#首一多项式

h = poly_gcd(f, g)
m1 = -h.constant_coefficient()#提取常数项
m = m1 - X1
print("Recovered message:", m)

RSA多组n，c，共用e

题目给了多组n，c，找到某两组n共享的p，可以求出q，从而变成一般的rsa问题

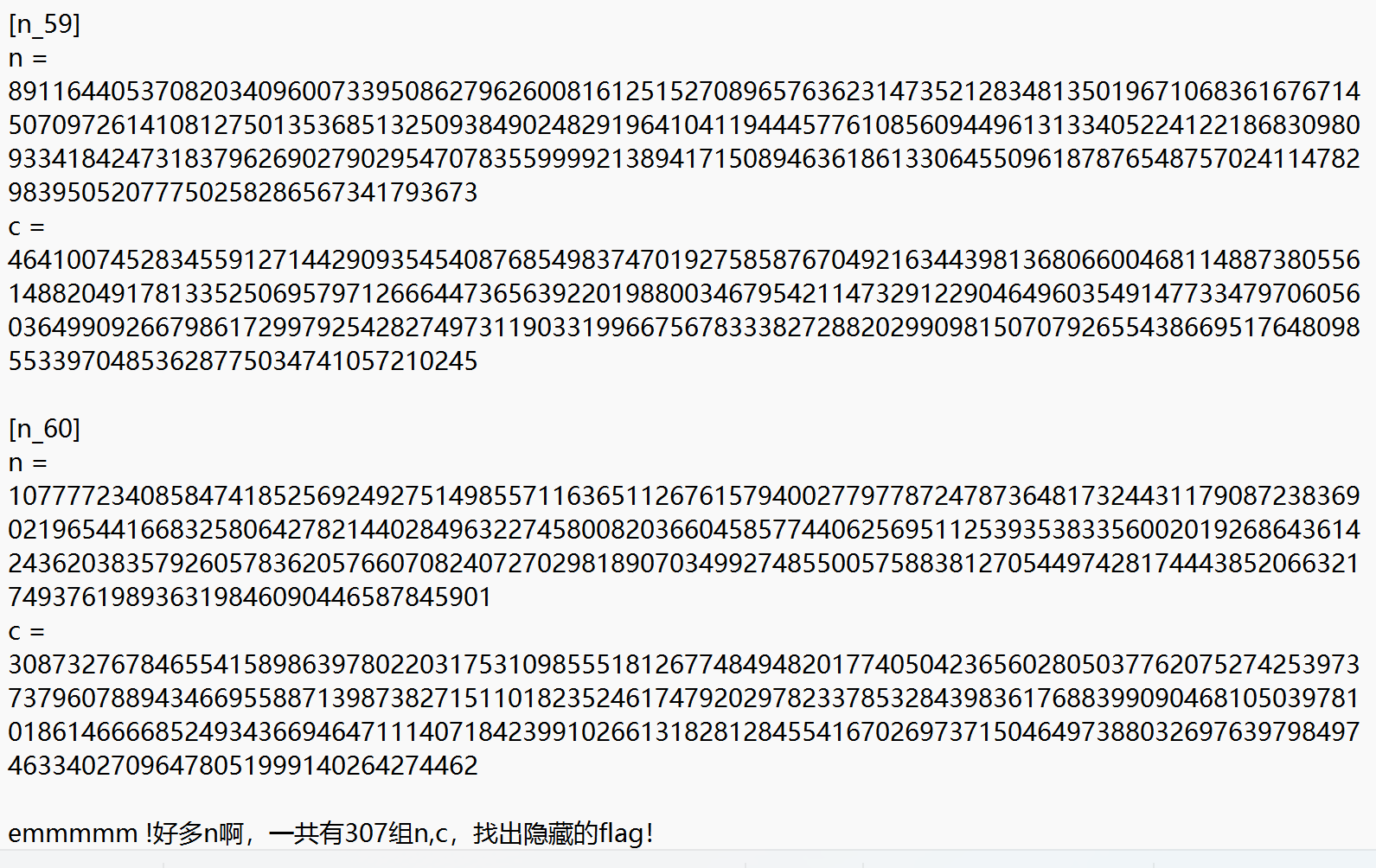
exp：

from gmpy2 import *
from Crypto.Util.number import *
n_list = []
c_list = []
e = 65537
with open("D:\\temp\\challenge (1).txt", "r", encoding="utf-8") as f:
    for line in f:
        if line.startswith("n ="):
            n = int(line.split("=")[1].strip())#将字符串按’=‘分成列表，取分割后第二部分，.strip()去除两端空白字符，int()将字符串转换为整数
            n_list.append(n)
        elif line.startswith("c ="):
            c = int(line.split("=")[1].strip())
            c_list.append(c)
for i in range(len(c_list)):
    for j in range(i+1,len(c_list)):
        if gcd(n_list[i],n_list[j])!=1:
            p=gcd(n_list[i],n_list[j])
            q=n_list[i]//p
            phi=(p-1)*(q-1)
            d=invert(e,phi)
            m=pow(c_list[i],d,n_list[i])
            flag=long_to_bytes(m)
            if b'TGCTF' in flag:
                print(flag)