NOIP 冲刺之——dp

\(\texttt{0x00}\) 前言

本篇文章主要记录笔者 NOIP 冲刺阶段复习的各种 dp 题型及 tricks ans tips，同时也用于及时复习与巩固。

那么，开始吧。

\(\texttt{0x01}\) 线性 dp

线性 dp 对我来说是一类很捉摸不定的题型：她太综合了，可以和任何知识点合起来考，这里就先抛开“数据结构优化”的成分展开来讲。

线性 dp 的状态设计不一定都是一维的，是指在状态转移时在每一维上是线性转移。就比如：

\[dp_i = dp_{i - j} + c_i \]

这种式子就是线性 dp 的大概模样。

如果很幸运，你看出一道题有线性 dp 的做法，那么可以从几个方向入手：

1. 观察数据范围，这通常可以启发状态设计；
2. 注意题目中具有明显线性转移的语句；

然后根据设计出的状态，通常只需根据转移方程依次循环每个维度即可求解。

还需要抓住主要矛盾：找出 dp 的阶段，然后把它丢到最外层循环去。

接下来来看几道例题：

Frog 1

首先发现青蛙只能跳一格或两格，所以可以设 \(dp_i\) 表示青蛙跳到第 \(i\) 格所需的最小总费用。那么状态转移方程就是：

\[dp_i = \min\{dp_{i - 2} + \lvert h_{i - 2} - h_i\rvert, dp_{i - 1} + \lvert h_{i - 1} - h_i\rvert\} \]

Vacation

一共有 \(3\) 种活动，且不能两天做相同的活动，那么我们可以这么定义状态：\(dp_{i, 0/1/2}\) 表示到第 \(i\) 天且前一天做了什么活动（\(0\) 表示在海里游泳，\(1\) 表示在山上抓虫，\(2\) 表示在家做作业）能获得的最大幸福值。

状态转移方程：

\[dp_{i, 0} = \max\{dp_{i - 1, 1}, dp_{i - 1, 2} + a_i\} \]

\[dp_{i, 1} = \max\{dp_{i - 1, 0}, dp_{i - 1, 2} + b_i\} \]

\[dp_{i, 2} = \max\{dp_{i - 1, 0}, dp_{i - 1, 1} + c_i\} \]

答案就是第 \(n\) 天时三种活动活动中的最大值。

其实这道题也是状态机模型 dp 的一道经典题目。

Coins

表面上是概率 dp，但不要被唬住了，本质上还是一道简单的线性 dp。

通过题目描述（主要）和数据范围（次要）可以大概确定状态是二维的，\(dp_{i, j}\) 表示考虑前 \(i\) 个硬币，有 \(j\) 个正面朝上的概率。

对于第 \(i\) 个硬币，有概率朝上或朝下，那就都讨论一遍，得出状态转移方程为：

\[dp_{i, j} = dp_{i - 1, j - 1}\times p_i + dp_{i - 1, j}\times (1 - p_i) \]

顺便地，线性 dp 有一个优化空间的小技巧：滚动数组（其实在其它类型的 dp 中有时也会用到）。

比如这一题，我们发现每次只会用到 \(dp_{i - 1}\) 这一层里的东西，且最后求总和时也只用到 \(dp_n\) 这一层，那么假设现在我们开始求第 \(2\) 层的 dp 值了，她只会用到 \(dp_1\) 这一层的东西，\(dp_0\) 就可以扔掉了，这样就可以保证在 dp 的过程中始终只会占用两层的空间，换句话说，空间复杂度从 \(O(n^2)\) 优化到了 \(O(n)\)。

加滚动数组优化也很简单，这里我们只需要两层，那么就在所有第一维的地方加上一个 & 1，就行了。同理，如果需要 \(k\) 层，就加上 & k - 1。

综上，状态转移方程就变为了：

\[dp_{i \wedge 1, j} = dp_{i - 1\wedge 1, j - 1}\times p_i + dp_{i - 1\wedge 1, j}\times (1 - p_i) \]

Candies

挺有意思的一道题。

首先朴素 dp 很好想，根据数据范围大概可以猜出状态设计：\(dp_{i, j}\) 表示考虑前 \(i\) 个人，现在还剩下 \(j\) 个糖果的方案数。

那么状态转移方程为：

\[dp_{i, j} = \sum\limits_{k = 0}^{\min(a_i, m - j)}dp_{i - 1, j + k} \]

但是这样转移时间复杂度是 \(O(\sum a_iK)\)，考虑优化。

这里我想了一个十分类似完全背包优化的方法。

发现有很多重复项，所以可以列出相邻的项找关系。

把 \(dp_{i, j}\) 和 \(dp_{i, j - 1}\) 的表达式写出来：

dp[i][j]   =                dp[i-1][j] + dp[i-1][j+1] + dp[i-1][j+2] + ... + dp[i-1][min(j+a[i]-1,m)] + dp[i-1][min(j+a[i],m)]

dp[i][j-1] = dp[i-1][j-1] + dp[i-1][j] + dp[i-1][j+1] + dp[i-1][j+2] + ... + dp[i-1][min(j+a[i]-1,m)]

会发现他们中间有很多项都是完全一样的，所以 \(j\) 每次减一的时候就只用去掉一个尾巴，加上一个头就可以了。

for(int i = 1; i <= n; i++)
    for(int j = K; ~j; j--)
        if(j + a[i] < K) dp[i][j] = ((ll)mod + dp[i][j + 1] + dp[i - 1][j] - dp[i - 1][j + a[i] + 1]) % mod;
        else dp[i][j] = (dp[i][j + 1] + dp[i - 1][j]) % mod;

P1541 [NOIP2010 提高组] 乌龟棋

根据数据范围题目描述不难猜到这个题是个多维度的线性 dp，直接来！

设已经使用了 \(a\) 张牌 \(1\)，\(b\) 张牌 \(2\)，\(c\) 张牌 \(3\)，\(d\) 张牌 \(4\) 所能获得的最大分数。

对于每一维都枚举一遍，设 \(v = a_{a + 2b + 3c + 4d}\)，那么状态转移方程为：

\[dp_{a, b, c, d} = \max(dp_{a, b, c, d}, dp_{a - 1, b, c, d} + v) \]

\[dp_{a, b, c, d} = \max(dp_{a, b, c, d}, dp_{a, b - 1, c, d} + v) \]

\[dp_{a, b, c, d} = \max(dp_{a, b, c, d}, dp_{a, b, c - 1, d} + v) \]

\[dp_{a, b, c, d} = \max(dp_{a, b, c, d}, dp_{a, b, c, d - 1} + v) \]

P11233 [CSP-S 2024] 染色

考场上犯糖了，不知道为什么跳了这道题，而且 20pts 的暴力也打挂了，可以说是一败涂地。

其实这道题还挺简单的，不管是暴力还是优化。

很显然的序列上线性 dp，先思考 \(O(n^2)\) 暴力。

设 \(dp_i\) 表示考虑前 \(i\) 位能获得的最大得分。

那么状态转移方程就为：\(dp_i = \max\limits_{1\le j < i}\{dp_j + val(j + 1, i)\}\)，\(val(i, j)\) 表示 \([i, j]\) 这段区间的贡献。

那么就可以 \(O(n^2)\) 预处理出所有的 \(val(i, j)\)，然后 \(O(n)\) 转移。

但是很快我们就认识到转移能优化成 \(O(1)\)，因为对于一个 \(i\)，选取她的左边第一个与她相同的位置转移一定是不劣的。

为什么呢？

因为 \(dp_i\) 的计算分为两步，第一步为 \(a_i\) 不产生贡献，即 \(dp_i = dp_{i - 1}\)，第二步为 \(a_i\) 产生贡献，那么只有左侧与其最靠近的同色的数 \(j\) 与 \(i\) 相同的才能对 \(dp_i\) 有贡献，这就限定了 \(a_j = a_i\)。

而且为了得到这个贡献也是不择手段——必须钦定区间 \([j + 1, i]\) 全为另一种颜色才行，也就是说，这一段区间里只有相邻且数值相同才能产生贡献，而且相邻且同色一定会被染成同色，这是因为将她俩染成同色不会影响其他任何东西。

令 \(pre_i\) 表示 \(a_i\) 左侧第一个等于 \(a_i\) 的位置，若 \(j\ne pre_i\) 的话，那么 \(val(j + 1, pre_i)\) 的非相邻的相同数的贡献就吃不到，而用 \(pre_i\) 转移的话就吃得到，而这种决策一定被 \(dp_{pre_i + 1}\) 包含，所以可以放心转移。

那么现在就可以将转移优化到 \(O(1)\)，但是预处理仍然是 \(O(n^2)\)，复杂度依然没有降下来。

注意到 \([j + 1, i]\) 这一段区间里只有相邻且数值相同才能产生贡献，所以不用开二维数组计算，直接一维前缀和即可。

综上所述，时间复杂度为 \(O(n)\)。

要特别注意！此时状态转移方程变成了：\(dp_i = \max\{dp_{i - 1}, dp_{pre_i + 1} + sum_{i - 1} - sum_{pre_i + 1} + a_i\}\)。

为什么是 \(dp_{pre_i + 1}\) 呢？因为若用 \(dp_{pre_i} + sum_{i - 1} - sum_{pre_i}\) 就没有统计到 \(pre_i + 1\) 的贡献，而这个贡献直接用前缀和数组是无法计算的（因为你无法知道 \(pre_i + 1\) 前面是否有一个数和她颜色数值都相同），但是 \(dp_{pre_i + 1}\) 就恰好包含了她而且是这种情况下的最优决策，所以应该用 \(dp_{pre_i + 1} + sum_{i - 1} - sum_{pre_i + 1}\) 来更新。

P1387 最大正方形

好像是一类比较有意思的题的最基础版本。

设 \(dp_{i, j}\) 表示以 \((i, j)\) 作为正方形的右下角时的最大边长。

那么可以看一下右下角的情况：

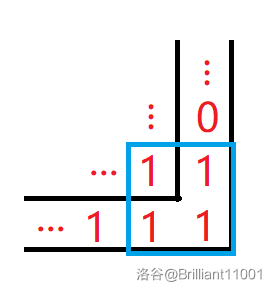
可以看到，首先 \(a_{i, j}\) 这一位必须要是 \(1\) 才能对 \(dp_{i, j}\) 有贡献，其次，以这这里作为正方形的右下角时的最大边长取决于能向左上扩展多少和向左扩展和向上扩展多少。

而向左上扩展多少就是 \(dp_{i - 1, j - 1}\)，向左扩展多少和向上扩展多少都可以 \(O(n^2)\) 预处理，但是在这道题中可以直接用 \(dp_{i - 1, j}\) 和 \(dp_{i, j - 1}\)（可以从决策包容性方面思考一下为什么）。

然后这道题的状态转移方程就推出来啦：

\[dp_{i, j} = \min\{dp_{i - 1, j - 1}, dp_{i - 1, j}, dp_{i, j - 1}\} + 1\space\space\space\space(a_{i, j} = 1) \]

P1736 创意吃鱼法

这道题是找最大的只有对角线是 \(1\) 的正方形。

同上一道题的思考方式，但是对角线有两个方向所以分开做。

设 \(f_{i, j}\) 表示以 \((i, j)\) 为右下角的只有左上到右下对角线有 \(1\) 的最大正方形的边长，\(g_{i, j}\) 表示以 \((i, j)\) 为右下角的只有左上到右下对角线有 \(1\) 的最大正方形的边长。

画图来看：

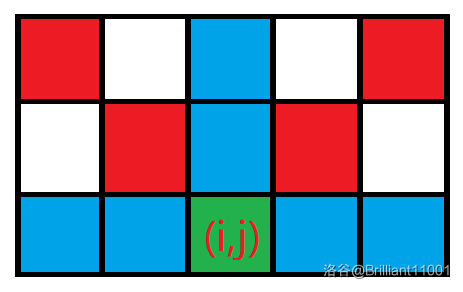
先考虑左边。

对于一个点 \((i, j)\)，她形成的最大正方形必须要求横竖都要为 \(0\)，记 \(l_{i, j}\) 表示 \((i, j)\) 左侧有多少个连续的 \(0\)，\(up_{i, j}\) 表示 \((i, j)\) 上方有多少个连续的 \(0\)，这两个都可以 \(O(n^2)\) 预处理出来。

那么状态转移方程为 \(f_{i, j} = \min\{f_{i - 1, j - 1}, l_{i, j}, up_{i, j}\} + 1\)。

\(g\) 的求法和 \(f\) 大同小异，再维护一个 \(r_{i, j}\) 表示表示 \((i, j)\) 右侧有多少个连续的 \(0\) 即可。

\(\texttt{0x02}\) 区间 dp

对于这种 dp 我都是类比线段树的合并来理解，一般有很明显的区间性，通常采用枚举分界点的方式来转移。

题目没时间贴了，咕咕咕……（反正考到了简单的能做，难的话也做不来）

\(\texttt{0x03}\) 树形 dp

和图论有明显的交集，可以借助图论的思想形象地思考问题和划分阶段，所以个人认为在某些方面比线性 dp 和区间 dp 好理解。

知识点 \(1\)：树上背包

来不及复习啦/qaq。

知识点 \(2\)：换根 dp

题单

对于这种题我建议先打暴力，然后在暴力的基础上做等价变换。

来回顾一下换根 dp 的基本思路：

1. 第一次 dfs，任选一个点为根进行方才的树形 dp；
2. 第二次 dfs，从相同的根出发，再扫描一遍从父节点向子结点更新信息，这里多半会用到剔除贡献的问题，要么记最大 / 次大值和具体从哪个点更新（这个主要用于最大 / 最小的不满足可减性的信息），要么从第一遍 dfs 的信息更新处倒推（这个一般用于满足可减性的信息）。

P3478 [POI2008] STA-Station

经典入坑题。

先打暴力，设 \(f_u\) 表示只考虑以 \(u\) 为根的子树，深度之和是多少，那么直接从底向上更新即可。

状态转移方程为：\(dp_u = \sum\limits_{v\in Son(u)}f_v + size_v\)

接着再换根，考虑父节点怎么更新子节点。

令 \(g_u\) 表示以 \(u\) 为根的深度之和（显然具有可减性），那么对于 \(u\) 的儿子 \(v\)，往下的深度和已经储存在 \(f_v\) 中，只需考虑向上走的贡献，为 \(g_u - f_v - size_v\)。然后假设将 \(u\) 转下来作为 \(v\) 的儿子的话，还需要加上 \((u, v)\) 这条边的贡献，也就是说，除去 \(\texttt{subtree(v)}\) 之外的所有点还要贡献 \(1\) 的深度。

综上，\(g_v = g_u - f_v - size_v + f_v + n - size_v = g_u + n - 2\times size_v\)。

二次扫描即可。

[ABC348E] Minimize Sum of Distances

经典变式题，推了一下发现就是把上一道题的 \(size\) 动了下手脚变成点权和即可。

P10974 Accumulation Degree

蓝书上的例题。

更好的阅读体验

题目传送门

题目大意：

给定一颗无根树，有一个节点是源点，度数为 \(1\) 的点是汇点，树上的边有最大流量。除源点和汇点外，其它点不储存水，即流入该点的水量之和等于从该点流出的水量之和。整个水系的流量定义为原点单位时间内能发出的水量。

现在需要求出：在流量不超过最大流量的前提下，选取哪个点作为源点，整个水系的流量最大，输出最大值。

思路：

朴素的想法是枚举某个点作为源点，然后做树形 dp，设 \(f_u\) 表示从点 \(u\) 往下流向子树的最大流量，不难得出状态转移方程：

\[f_u = \sum\limits_{j\in Son(u)}\begin{cases}\min(w_i, f_j) & \deg_j > 1\\w_i & \deg_j = 1\end{cases} \]

对于每个点都这样做一遍，取 \(\max\)，时间复杂度 \(O(n^2)\)。

因为这个题是一个无根树，而我们又要枚举根节点，所以不难想到用换根 dp 来代替源点的枚举。

所以考虑用换根 dp 来优化。

对应到这个题上就是思考子节点流向父节点的信息怎么计算。

先画个图：

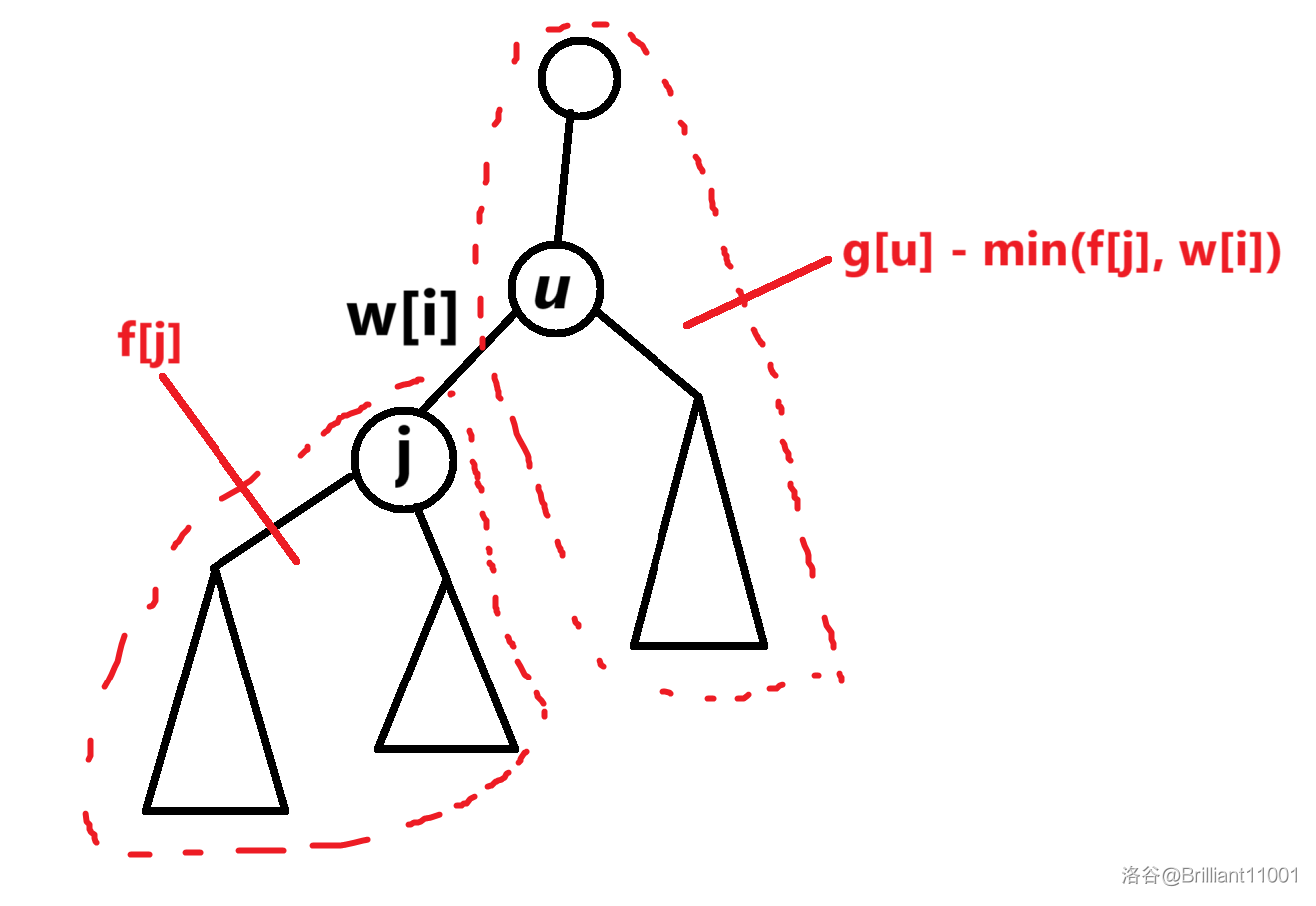
这里 \(g_u\) 表示 \(u\) 为源点的最大流量。

这道题的信息显然具有可减性。

如图，我们可以考虑先去掉 \(j\) 子树对 \(g_u\) 的贡献得到以 \(u\) 为源点的其他贡献，然后这一部分实际就是从 \(j\) 往上流的最大流量，直接和 \(f_j\) 相加就得到了 \(g_j\)。

但是这里有个魔鬼细节，需要考虑节点的度数，因为度数为 \(1\) 的点在第一遍 dfs 时是直接加上的 \(w_i\)，所以在去掉贡献的时候需要判一下。父节点也基本同理。

那么这道题就结束了，时间复杂度 \(O(n)\)。

P11324 【MX-S7-T2】「SMOI-R2」Speaker

今天打的梦熊模拟赛的题，考场上忘了换根 dp 怎么写，所以只用 \(O(n^2)\) 骗了 52 pts……（话说这道题怎么还不升蓝）

暴力做法：

画个图理解一下：

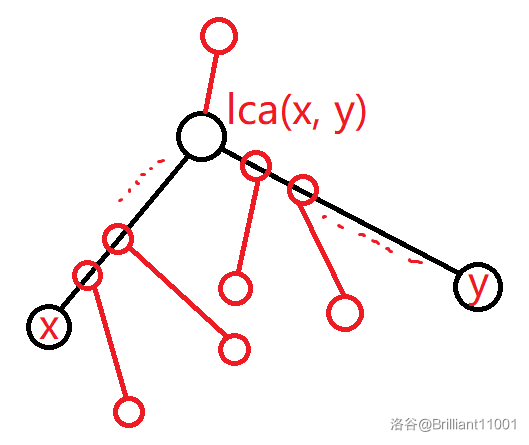
不难发现每个询问其实就是询问 \(a\rightarrow b\) 这条路径上所有点中能走出去获得的最大值。具体而言，就是在这条路径上找到一个点 \(z\) 使得存在一个 \(z\) 能走到的 \(t\) 且 \(v_t - 2\times dist(z, t)\) 最大。

那么对于每个点都与处理出这样的 \(t\)，相当于做 \(n\) 遍树形 dp，然后将每个点的这个最大值记为 \(mxdis\) 挂到这个点上，跑一遍倍增 lca，求路径最大值即可。

时间复杂度 \(O(n^2)\sim O(\log n)\)。

发现时间复杂度瓶颈在于求 \(mxdis\) 数组，考虑用换根 dp 优化。

这个信息不满足可减性，所以需要用记录记最大 / 次大值和具体从哪个点更新。

记 \(dp_{u, 0/1}\) 分别表示以 \(u\) 为起点向下走的最大 / 次大值，\(up_u\) 表示以 \(u\) 为起点向上走的最大值。

画图理解一下：

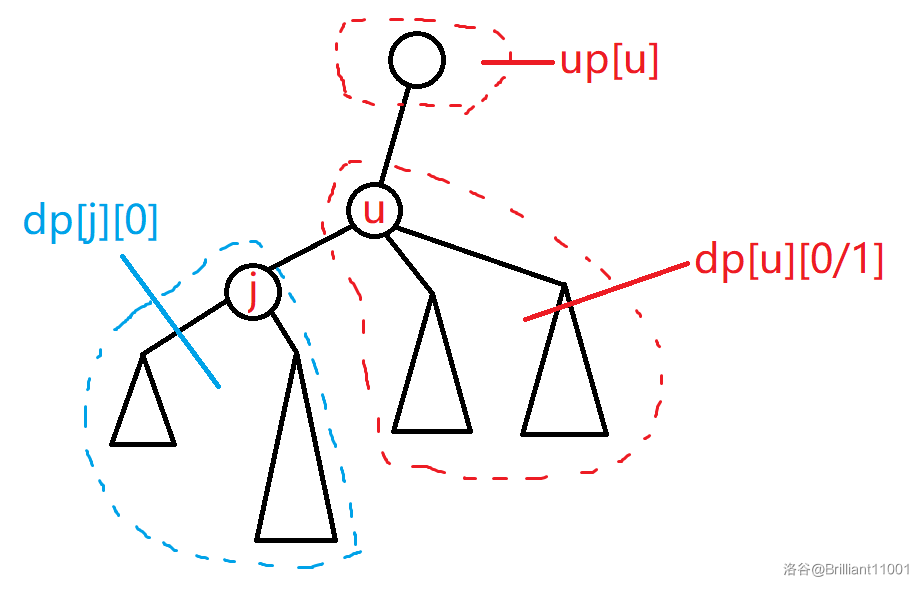
若 \(u\) 的最大值时从 \(j\) 更新过来的，那么右下的虚线框内就取 \(dp_{u, 1}\)，否则取 \(dp_{u, 0}\)，那么 \(mxdis_j\) 就的值为这三部分与 \(v_u\) 取 \(\max\)。

为什么还要与 \(v_u\) 取 \(\max\)？因为这些状态都没有包括起点的权值，但是存在一种走法：只从 \(j\rightarrow u\)。

综上，先 dfs 两次求出 \(mxdis\)，再树上倍增预处理 lca 和路径最大值，总复杂度 \(O((n + q)\log n)\)。

其他：

咕咕咕……

\(\texttt{0x04}\) 数据结构优化 dp

P2569 [SCOI2010] 股票交易

先想暴力，设 \(dp_{i, j}\) 表示到第 \(i\) 天，现在手上还有 \(j\) 股，能获得的最大利润，设交易冷却期为 \(W\)。

将当前的操作分为四种：

1. 空仓买入；
2. 持股不操作；
3. 持股买入；
4. 卖出。

第一种操作就是赋初始值：\(dp_{i, j} = -ap_i\times j\)；

第二种操作就是继承上一个状态：\(dp_{i, j} = dp_{i - 1, j}\)，这个更新至关重要的一点是她为后来的操作提供了方便；

第三种操作从背包的角度考虑，设买入了 \(k\) 股，那么转移方程为：\(dp_{i, j} = dp_{i - W - 1, j - k} - k\times ap_i\)。注意！这里之所以没用 \(1\sim i - W - 1\) 转移是因为我们在第二种操作时就已经包含了前面几天的所有决策，所以直接用 \(i - W - 1\) 转移就行了。

第四种操作类似，设卖出了 \(k\) 股，那么转移方程为：\(dp_{i, j} = dp_{i - W - 1, j + k} + k\times bp_i\)。

这样是 \(O(n^3)\) 的，考虑优化。

发现当 \(j\) 增加 \(1\) 时只增加了一个决策 \(dp_{i - W - 1, j}\) 同时可能减少若干决策，所以可以往单调队列优化的方向思考。

将操作 \(3,4\) 的式子转化一下，得：

操作 \(3\)：\(dp_{i, j} + j\times ap_i = dp_{i - W - 1, k} + (j - k)\times ap_i\)

操作 \(4\)：\(dp_{i, j} + j\times ap_i = dp_{i - W - 1, j + k} + (j + k)\times bp_i\)

对于操作 \(3\)，将 \(dp_{i, j} + j\times ap_i\) 看作一个整体，相当于求滑动窗口区间最大值，就可以用单调队列维护了，操作 \(4\) 也是同理。

P2344 [USACO11FEB] Generic Cow Protests G

先推方程：\(dp_i = \sum\limits_{j = 0}^{i - 1}dp_{j}[sum_i\ge sum_j]\)。

直接转移显然是 \(O(n^2)\) 的（但是这样也拿 90pts，数据太水了），观察到对 \(dp_i\) 产生贡献的 \(j\) 满足：\(j < i,sum_j\le sum_i\)，所以转换成二维偏序用树状数组优化转移就行了。

需要尤其注意！树状数组的下标不能为 \(0\)，否则会死循环，所以离散化的时候要把下标 \(+1\)。