二叉搜索树(BST)
二叉搜索树的定义及性质
二叉搜索树(\(\texttt{Binaty Search Tree}\))简称 \(\texttt{BST}\),它拥有“\(\texttt{BST}\) 性质”,这也是平衡树的基础。
给定一棵二叉树,树上的每一个节点带有一个权值。所谓“\(\texttt{BST}\) 性质”是指,对于树中的任意一个节点:
- 该节点的权值不小于它的左子树中任意节点的权值;
- 该结点的权值不大于它的右子树中任意节点的权值。
满足上述性质的二叉树就是一棵 “二叉查找树”(\(\texttt{BST}\))。
比如:
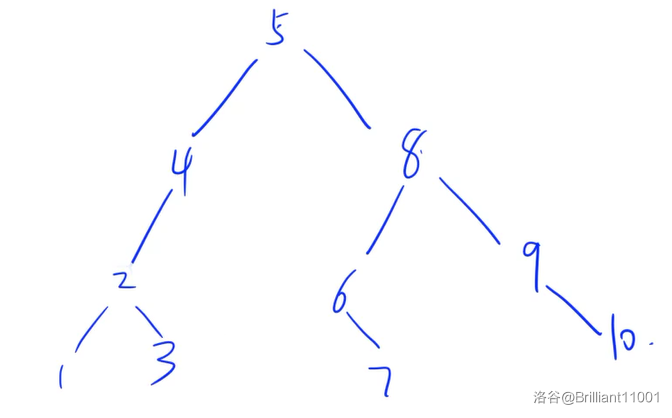
同时珂以发现,它的中序遍历为 \(\{1,2,3,4,5,6,7,8,9,10\}\),就是将这所有权值从小到大排序后的结果。
二叉搜索树的一些操作
1. 建立
为了避免越界,减少边界情况的特殊判断,一般在 \(\texttt{BST}\) 中额外插入一个权值为 \(+\infty\) 和一个权值为 \(-\infty\) 的节点。
仅由这两个节点构成的 \(\texttt{BST}\) 就是一棵初始的空的 \(\texttt{BST}\)。
为了方便起见,在接下来的操作中,假设 \(\texttt{BST}\) 不会含有权值相同的节点(即使有也可以用一个 \(cnt\) 数组记录出现的次数)。
struct BST {
int ls, rs;
int val;
int cnt;
int siz;
}a[N];
int tot, root, inf = 0x7fffffff;
int New(int val) {
a[++tot].val = val;
return tot;
}
void build() {
New(-inf);
New(inf);
root = 1, a[1].rs = 2;
}
2. 检索
这个比较简单,就不放代码了,只给出思路。
假如说要找一个权值为 \(val\) 的节点。
设当前搜索到的节点为 \(p\),则一开始 \(p = root = 1\)。
-
若 \(a[p].val == val\),则已经找到;
-
若 \(a[p].val < val\)
(1)若 \(p\) 无左子节点,则说明不存在 \(val\)。
(2)若 \(p\) 有左子节点,则继续检索 \(p\) 的左子树。
-
若 \(a[p].val > val\),
(1)若 \(p\) 无右子节点,则说明不存在 \(val\)。
(2)若 \(p\) 有右子节点,则继续检索 \(p\) 的右子树。
3. 插入
在 \(\texttt{BST}\) 中插入一个新的值 \(val\)。
与 \(\texttt{BST}\) 的检索过程相似。
在发现要走向的 \(p\) 无子节点,说明 \(val\) 不存在时,直接建立权值为 \(val\) 的新节点作为 \(p\) 的新节点。
void insert(int &p, int val) { //注意p是引用,其父节点的 l 或 r 值会被同时更新
if(p == 0) {
p = New(val);
return ;
}
if(val == a[p].val) {
a[p].cnt++;
return ;
}
if(val < a[p].val) insert(a[p].l, val);
else insert(a[p].r, val);
}
4. 求前驱/后缀
\(val\) 的前驱是指在 \(\texttt{BST}\) 中权值小于 \(val\) 中的权值中最大的那个。同理,\(val\) 的后继是指在 \(\texttt{BST}\) 中权值大于 \(val\) 中的权值中最小的那个。
以求前驱为例,先初始化 \(ans\) 为权值为 \(+\infty\) 的那个节点的编号,然后在 \(\texttt{BST}\) 中检索 \(val\)。在检索过程中,每经过一个节点 \(p\),都尝试能不能让它更新\(ans\) 作为要求的前驱的候选答案。
检索完成后,有三种可能的结果:
-
没有找到 \(val\),则 \(val\) 的前驱就是 \(ans\)。
-
找到了权值为 \(val\) 的节点 \(p\),但是 \(p\) 没有左子树,则 \(val\) 无前驱,\(ans\) 还是答案。
-
找到了权值为 \(val\) 的节点 \(p\),且 \(p\) 有左子树,则说明答案是 \(p\) 左子树中的最大值,从 \(p\) 的左子节点出发,然后一直向右走,就找到了答案。
int get_pre(int val) { //求前驱
int ans = 1; //a[1].val = -0x7fffffff
int p = root;
while(p) {
if(val == a[p].val) { //检索成功
if(a[p].ls) {
p = a[p].ls; //从左子节点出发
while(a[p].rs) p = a[p].rs; //一直向右走
ans = p;
}
break;
}
//每经过一个点,都尝试更新前驱
if(val > a[p].val && a[p].val > a[ans].val) ans = p;
p = val > a[p].val ? a[p].rs : a[p].ls; //检索
}
return ans;
}
int get_next(int val) { //求后继
int ans = 2; //a[2].val = 0x7fffffff
int p = root;
while(p) {
if(val == a[p].val) {
if(a[p].rs) {
p = a[p].rs;
while(a[p].ls) p = a[p].ls;
ans = p;
}
break;
}
if(val < a[p].val && a[p].val < a[ans].val) ans = p;
p = val > a[p].val ? a[p].rs : a[p].ls;
}
return ans;
}
//递归写法
int get_pre(int p, int val) {
if(!p) return -inf;
if(val <= tr[p].val) return get_pre(tr[p].ls, val);
return max(tr[p].val, get_pre(tr[p].rs, val));
}
int get_next(int p, int val) {
if(!p) return inf;
if(val >= tr[p].val) return get_next(tr[p].rs, val);
return min(tr[p].val, get_next(tr[p].ls, val));
}
5. 删除
从 \(\texttt{BST}\) 中删除权值为 \(val\) 的节点。
首先通过检索找到权值为 \(val\) 的节点 \(p\)。
若 \(p\) 是叶节点,则直接删除就行了。
若 \(p\) 有一个儿子,则删除 \(p\),再让 \(p\) 的儿子代替 \(p\) 的位置。
若 \(p\) 有两个儿子,就有点麻烦了,要先求出 \(val\) 的后继节点 \(next\),因为 \(next\) 无左子树,所以可以直接删除 \(next\),并让 \(next\) 的右子树代替 \(next\) 的位置,再让 \(next\) 代替 \(p\) 的位置,删除 \(p\) 即可。
void remove(int &p, int val) {
if(p == 0) return ;
if(val == a[p].val) {
if(!a[p].ls) p = a[p].rs; //没有左子树,则右子树代替 p 的位置,注意 p 是引用
else if(!a[p].rs) p = a[p].ls; //没有右子树,则左子树代替 p 的位置,注意 p 是引用
else { //有两个儿子
//求后继节点
int next = a[p].rs;
while(a[next].ls > 0) next = a[next].ls;
//next 一定无左子树
remove(a[p].rs, a[next].val);
//让节点 next 代替节点 p 的位置
a[next].ls = a[p].ls, a[next].rs = a[p].rs;
p = next;
}
return ;
}
if(val < a[p].val) remove(a[p].ls, val);
else remove(a[p].rs, val);
}
二叉搜索树的时间复杂度
在随机数据中,\(\texttt{BST}\) 一次操作的期望时间复杂度为 \(O(\log n)\),但是,要是按照顺序向 \(\texttt{BST}\) 中插入一个有序序列,\(\texttt{BST}\) 就会退化成一条链,这时候平均每次操作的时间复杂度就会变为 \(O(n)\)。这时候我们称这种左右子树大小相差很大的 \(\texttt{BXT}\) 是“不平衡”的。
而为了维持 \(\texttt{BST}\) 的平衡,就产生了许多数据结构,我们称之为平衡树。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号