高级数据结构（一）树状数组

引入

根据任意正整数关于 \(2\) 的不重复次幂的唯一分解原理性质，若一个正整数 \(x\) 的二进制表示为 \(a_{k - 1}a_{k - 2}\cdots a_2a_1a_0\)，其中等于 \(1\) 的位是 \(\{a_{i_1},a_{i_2},\cdots ,a_{i_m}\}\)，则正整数 \(x\) 可以被二进制分解为：

\[x = 2^{i_1} + 2^{i_2} + \cdots + 2^{i_m} \]

其中，\(m \le \log k\)

不妨设 \(i_1 > i_2 > \cdots > i_m\)，进一步地，区间 \([1,x]\) 可以分成 \(O(\log x)\) 个小区间：

1. 长度为 \(2^{i_1}\) 的小区间 \([1,2^{i_1}]\)
2. 长度为 \(2^{i_2}\) 的小区间 \([2^{i_1} + 1,2^{i_1} + 2^{i_2}]\)
3. 长度为 \(2^{i_3}\) 的小区间 \([2^{i_1} + 2^{i_2} + 1,2^{i_1} + 2^{i_2} + 2^{i_3}]\)

\(\cdots \cdots\)

m. 长度为 \(2^{i_m}\) 的小区间 \([2^{i_1} + 2^{i_2} + \cdots + 2^{i_{m - 1}} + 1,2^{i_1} + 2^{i_2} + \cdots + 2^{i_m}]\)

这些小区间的共同特点是：若区间结尾为 \(R\)，则区间长度就等于 \(R\) 的“二进制分解”下最小的 \(2\) 的次幂，即 \(\texttt {lowbit(R)}\)。例如 \(x = 7 = 2^2 + 2^1 + 2^0\)，区间 \([1,7]\) 可以分成 \([1,4],[5,6]\) 和 \([7,7]\) 三个小区间，长度分别是 \(\texttt {lowbit(4)} = 4,\texttt {lowbit(6)} = 2,\texttt {lowbit(7) = 1}\)

给定一个整数 \(x\)，下面这段代码可以计算出区间 \([1,x]\) 分成的 \(O(\log x)\) 个小区间。

while(x > 0) {
	printf("[%d, %d]\n", x - (x & -x) + 1, x);
	x -= x & -x;
}

---

1.树状数组简介

树状数组（\(\texttt {Binary Indexed Trees}\)）就是一种基于上述思想的数据结构。

树状数组支持的操作：

1. 区间和、区间异或和、区间乘积和 RMQ（显然，支持的操作都具有交换律，这也算是树状数组的一大特性吧）

2. 单点修改（朴素的树状数组结构不支持区间修改，当然也可以普及成区间修改结构）

功能听起来和前缀和数组有点像，但它的优势在哪呢？

以求区间和为例，我们知道，前缀和数组求区间和的时间复杂度为 \(O(n)\)，单点修改操作的时间复杂度为 \(O(1)\)，所以对于 \(m\) 次询问，总时间复杂度为 \(O(mn)\)。

树状数组平均了一下，两种操作的时间复杂度都是 \(O(\log n)\)，所以对于 \(m\) 次询问，总时间复杂度为 \(O(m\log n)\)，比前缀和数组快上许多。

2.树状数组的存储特点：

对于给定的序列 \(a\)，我们建立一个数组 \(c\)，其中 \(c[x]\) 保存序列 \(a\)，的区间 \([x - lowbit(x) + 1,x]\) 中所有数的和，即 \(\sum ^x_{i = x - lowbit(x) + 1} a[i]\)。

为什么它叫做树状数组呢？事实上，数组 \(c\) 可以看作一个如下图所示的树形结构，图中最下边一行是 \(N\) 个叶节点（\(N = 8\)），代表数值 \(a[1\sim N]\)。该结构满足以下性质：

1. 每个内部节点 \(c[x]\) 保存以它为根的子树中所有叶结点的和；
2. 每个内部节点 \(c[x]\) 的子节点个数等于 \(\texttt {lowbit(x)}\) 的位数；
3. 除树根外，每个内部节点 \(c[x]\) 的父节点是 \(c[x + \texttt {lowbit(x)}]\)；
4. 树的深度为 \(O(\log N)\)
   如果 \(N\) 不是 \(2\) 的整次幂，那么树状数组就是一个具有同样性质的森林结构。

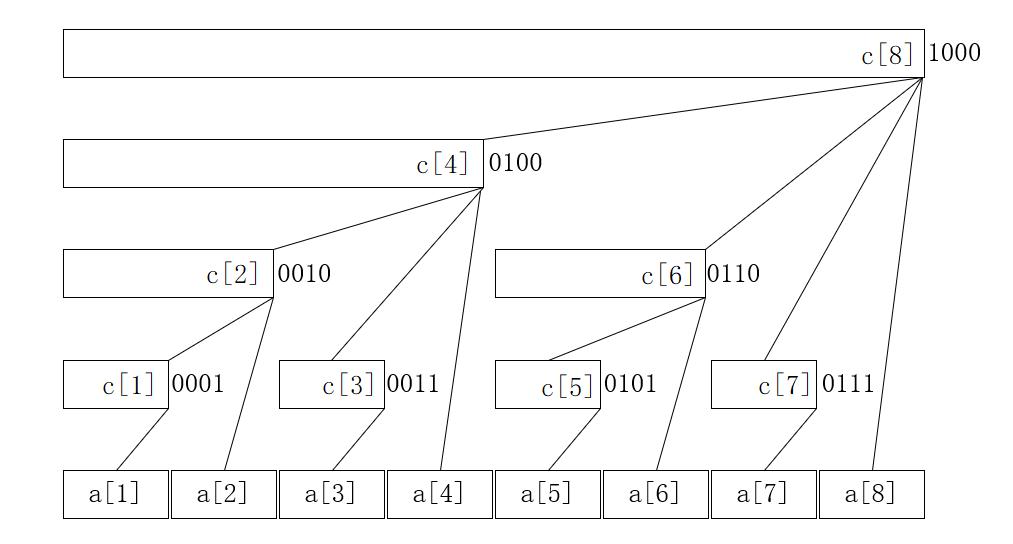
由图可知:

\(c[8] = c[4] + c[6] + c[7] + c[8]\)

\(c[7] = c[7]\)

\(c[6] = c[5] + c[6]\)

\(\cdots \cdots\)

3.树状数组的实现

在执行所有操作之前，我们需要对树状数组进行初始化——针对原始序列 \(a\) 构造一个树状数组。

为了简便起见，比较一般的初始化方法是：直接建立一个全为 \(0\) 的数组 \(c\)，然后对每个位置 \(x\) 执行 \(\texttt {add(x,a[x])}\)，就完成了对原始序列 \(a\) 构造树状数组的过程，时间复杂度为 \(O(n\log n)\)。通常采用这种方法已经足够。

更高效的初始化方法是：从小到大依次考虑每个节点 \(x\)，借助 \(\texttt{lowbit}\) 运算扫描它的子节点并求和。若采用这种方法，上面树形结构中的每条边只会被遍历一次，时间复杂度为 \(O(\sum ^{\log N} _{k = 1} k * N / 2^k) = O(n)\)。

快速初始化：

void init() {
    for (int i = 1; i <= n; i++) {
        pre[i] = pre[i - 1] + a[i];
        c[i] = pre[i] - pre[i - lowbit(i)];
    }
}

---

查询前缀和：

int ask(int x) {
	int res = 0;
	for(; x; x -= lowbit(x)) res += c[x];
	return res;
}

---

单点修改：

void add(int x, int y) {
	for(; x <= n; x += lowbit(x)) c[x] += y;
}

P3374 【模板】树状数组 1

---

单点询问 + 区间修改：

利用了差分的思想，维护一个差分数组 \(c\)，对于指令：把 \([x,y]\) 上的每一个数加上 \(k\)，就可转化成把 \(c[x]\) 加上 \(k\)，再把 \(c[y + 1]\) 减去 \(k\)。

P3368 【模板】树状数组 2

---

区间询问 + 区间修改：

（话说这不就是线段树吗）

说实话，树状数组不仅跑得比线段树快，码量要比线段树小得多，就是比较难想。

P3372 【模板】线段树 1

P2357 守墓人

#include <iostream>

using namespace std;

const int N = 5000010;
typedef long long ll;
int n, m;
ll c[2][N];

int lowbit(int x) {
	return x & -x;
}

ll ask(int id, int x) {
	ll res = 0;
	for(; x; x -= lowbit(x)) res += c[id][x];
	return res;
}

void add(int id, int x, ll y) {
	for(; x <= n; x += lowbit(x)) c[id][x] += y;
}

int main() {
	scanf("%d%d", &n, &m);
	ll a, las = 0;
	for(int i = 1; i <= n; i++) {
		scanf("%lld", &a);
		add(0, i, a - las);
		add(1, i, (i - 1) * (a - las));
		las = a;
	}
	int op, x, y;
	ll k;
	while(m--) {
		scanf("%d%d%d", &op, &x, &y);
		if(op == 1) {
			scanf("%lld", &k);
			add(0, x, k);
			add(0, y + 1, -k);
			add(1, x, (x - 1) * k);
			add(1, y + 1, -y * k);
		}
		else {
			printf("%lld\n", y * ask(0, y) - ask(1, y) - (x - 1) * ask(0, x - 1) + ask(1, x - 1));
		}
	}
	return 0;
}