从零开始掌握线段树大法
简介:
线段树(\(\texttt {Segment Tree}\)) 是一种高级数据结构,是一种基于分治思想的二叉树结构,主要用来处理区间问题。它可以在 \(O(\log n)\) 的时间复杂度内维护序列中满足结合律的变量,例如:\(\max\),\(\min\),\(\sum\) 和 \(\oplus\)。总的说来还是一个功能非常强大的数据结构,也有许多拓展。
下面就来逐步揭开线段树的神秘面纱。
1.线段树的基本知识及操作
线段树的本质是一棵二叉树,它有以下特性:
- 线段树的每个节点都代表一个区间;
- 线段树具有唯一的根结点,代表的区间是整个统计范围,如 \([1,N]\);
- 线段树的每个叶子节点都代表一个长度为 \(1\) 的元区间(元线段)\([x,x]\);
- 对于每个内部节点 \([l,r]\),它的左子结点是 \([l,mid]\),右子节点是 \([mid + 1,r]\),其中 \(mid = \lfloor\frac{l + r}{2}\rfloor\),这样也保证了线段树对区间包括地不重不漏。
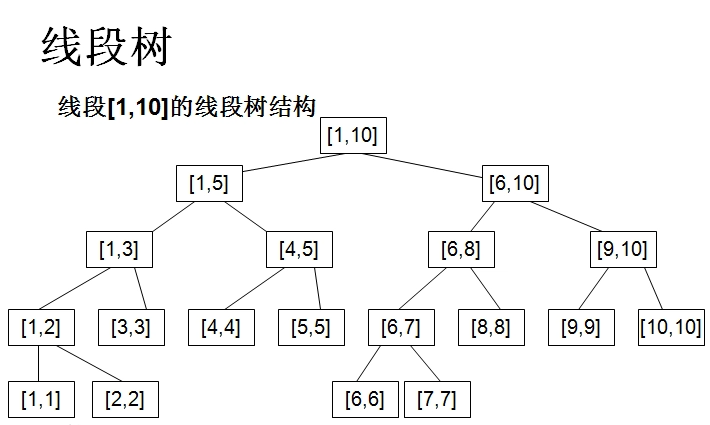
其实还是非常的形象,我们可以发现,除去最后一层,整棵线段树是一棵满二叉树,树的深度是 \(O(\log n)\),因此我们可以按照与二叉堆类似的 “父子 \(2\) 倍”节点编号的方法。
- 根节点编号为 \(1\);
- 编号为 \(x\) 的节点的左子结点编号为 \(x * 2\),右子节点编号为 \(x * 2 + 1\)。
这样一来,就可以用结构体来存储树中的信息。这里要注意:在理想情况下,\(N\) 个节点的满二叉树有 \(N + N / 2 + N / 4 + \cdots + 2 + 1 = 2N - 1\) 个节点。因为在这种存储方式下,最后一行会产生空余,最后一行会有 \(2N\) 个空间,所以保存线段树的数组长度要不小于 \(4N\),才能保证不会越界。
struct SegmentTree{
int l, r, data;
}tr[N << 2];
以下都以维护区间最大值为例。
建树
其实根据上面的图,思路已经很明了了:就是递归。
\(\texttt{Code}:\)
void build(int p, int l, int r) {
tr[p].l = l, tr[u].r = r;
if(l == r) {
tr[p].maxx = a[l];
return ; //叶子结点
}
int mid = l + r >> 1;
build(p << 1, l , mid); //建左子树
build(p << 1 | 1, mid + 1, r); //建右子树
tr[p].maxx = max(tr[p << 1].maxx, tr[p << 1 | 1].maxx);//整合子节点的信息,即后文的 pushup 函数
}
单点修改
单点修改是一条类似 \(\texttt{"C x v"}\) 的指令,表示把 \(A[x]\) 的值修改为 \(v\)。
在线段树中,根节点(编号为 \(1\) 的节点)是所有指令的入口。所以从根节点开始,递归找到代表 \([x,x]\) 区间的叶子节点,并把其值更新。由于递归时会先到达底端,再向上回溯,所以我们可以在回溯时顺便在父节点整合子节点的信息。时间复杂度为 \(O(\log n)\)。
\(\texttt{Code}:\)
void change(int p, int x, int val) {
if(l(p) == r(p)) {
maxx(p) = val;
return ;
}
int mid = l(p) + r(p) >> 1;
if(x <= mid) change(ls(p), x, val); //递归左儿子
else change(rs(p), x, val); //递归右儿子
pushup(p); //整合信息
}
change(1, x, v); //调用入口
\(\texttt{update on 2025.1.22}\):
其实因为常数问题,一般不用线段树做单点修改,而使用常数更小的树状数组来代替她,但是有的时候也不得不写(比如要使用线段树完成很多操作,其中包括单点修改,这时候当然就不好再多开一个树状数组了)。
但是常数比这种写法小的肯定是有的。
首先不难发现从上往下递归只是为了寻找要修改的节点,这个其实完全可以省略,只需要在建树的时候加上一句 \(id[l] = u\),在修改 \([x, x]\) 时直接修改 \(tr[id[x]]\) 的信息,然后再从下往上整合信息即可。
整个过程其实不需要递归(递归不知道要比循环常数大到哪里去了),只是多使用了一个数组和循环就能解决问题,虽然复杂度没变,但大大提高了运行的效率。
\(\texttt{Code}\):
void modify(int x, int v) {
int u = id[x];
maxx(u) = v;
while(u) {
u >>= 1;
pushup(u);
}
}
区间查询
单点修改是一条类似 \(\texttt{"Q l r"}\) 的指令,例如查询序列 \(A\) 在区间 \([l,r]\) 上的最大值,即\(\max_{l\le i\le r}A[i]\)。同样的,我们只需要从根节点开始,递归执行以下过程即可:
- 若 \([l,r]\) 完全覆盖了当前节点代表的区间,就可以直接返回该节点的信息。
- 若左儿子与 \([l,r]\) 有交集,则递归到左儿子。
- 若右儿子与 \([l,r]\) 有交集,则递归到右儿子。
\(\texttt{Code}:\)
int query(int p, int l, int r) {
if(l <= l(p) && r >= r(p)) return maxx(p);
int res = -(1 << 30);
int mid = l(p) + r(p) >> 1;
if(l <= mid) res = max(res, query(ls(p), l, r));
if(r > mid) res = max(res, query(rs(p), l, r));
return res;
}
该查询过程会把询问区间在线段树上分成 \(O(\log n)\) 个节点,所以时间复杂度为 \(O(\log n)\)。
为什们呢?我们不妨分类讨论一下:
\(1. \space\space l \le p_l\le p_r \le r\),则此时完全覆盖了当前节点,直接返回。
\(2. \space\space p_l\le l\le p_r\le r\),此时只有 \(l\) 处于节点之内,则:
\(\space\space\space\space\) (1)\(\space\space l > r\),只会递归右子树
\(\space\space\space\space\) (2)\(\space\space l \le r\),虽然递归两棵子树,但是右儿子会在递归后直接返回。
\(3. \space\space l\le p_l\le r\le p_r\),即只有 \(r\) 处于节点之内,与情况 \(2\) 类似。
\(4. \space\space p_l\le l\le r\le p_r\),即 \(l\) 和 \(r\) 都位于节点之内。
\(\space\space\space\space\) (1)\(\space\space l,r\) 都位于 \(mid\) 的一侧,只会递归一棵子树。
\(\space\space\space\space\) (2)\(\space\space l,r\) 分别位于 \(mid\) 的两侧,递归左右两棵子树。
也就是说,只有情况 \(4(2)\) 会真正产生对左右两棵子树的递归。这种情况至多发生一次,之后在子结点上就会变成情况 \(2\) 或 \(3\)。因此,上述查询过程的时间复杂度为 \(O(2\log n) = O(\log n)\)。从宏观上理解,相当于 \(l,r\) 两个端点分别在线段树上划分一条递归访问路径,情况 \(4(2)\) 在两条路径与从下往上的第一次交会处产生。
区间修改
这种情况就要比单点修改棘手一点,毕竟要比人家多改很多点,但时间复杂度还要在一个数量级,确实不简单。
试想一下,某个非叶子节点被修改区间 \([l,r]\) 完全覆盖,若直接从上到下传导修改信息,那么以该节点为根的子树就要全部被修改,时间按复杂度 \(O(n)\),这是我们不能接受的。
再试想,对于一次区间修改如果我们发现某个节点 \(p\) 所代表的区间被查询区间 \([l,r]\) 完全覆盖,并将此子树 \(p\) 全部更新。但是在之后的查询操作中却完全没有用到 \([l,r]\) 的子区间的信息,那么更新整棵子树就是徒劳。
那怎么办呢?这时候就需要引入一个新的东西:“延迟标记”,又叫做 \(\texttt{lazy tag}\),来标识“该节点曾经被修改,但其子节点尚未被更新”。
如果在后续的指令中,需要从节点 \(p\) 、向下递归,我们再检查 \(p\) 是否有标记。若有标记,就先把 \(p\) 的子节点更新,给两个子节点打上标记,再把 \(p\) 的标记消除。
这样一来,除了在修改指令中直接划分的 \(O(\log n)\) 个节点之外,对任意节点修改都延迟到“在后续操作中递归进入它的父节点时”在执行。每条查询或修改操作的时间复杂度都降低到了 \(O(\log n)\)。
2. 例题
【模板】线段树 1
\(\texttt{Code}:\)
#include <iostream>
using namespace std;
const int N = 100010;
typedef long long ll;
struct SegmentTree {
int l, r;
ll sum, add;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
#define add(x) tr[x].add
}tr[N * 4];
int n, m;
ll a[N];
void build(int p, int l, int r) {
l(p) = l, r(p) = r;
if(l == r) { sum(p) = a[l]; return ; }
int mid = l + r >> 1;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
sum(p) = sum(p * 2) + sum(p * 2 + 1);
}
void spread(int p) {
if(add(p)) {
sum(p * 2) += add(p) * (r(p * 2) - l(p * 2) + 1);
sum(p * 2 + 1) += add(p) * (r(p * 2 + 1) - l(p * 2 + 1) + 1); //更新子节点
add(p * 2) += add(p);
add(p * 2 + 1) += add(p); //下传标记
add(p) = 0; //消除父节点的标记
}
}
void change(int p, int l, int r, ll val) {
if(l <= l(p) && r >= r(p)) { sum(p) += val * (r(p) - l(p) + 1), add(p) += val; return ; } //完全包含
spread(p); //下传懒标记
int mid = l(p) + r(p) >> 1;
if(l <= mid) change(p * 2, l, r, val);
if(r > mid) change(p * 2 + 1, l, r, val);
sum(p) = sum(p * 2) + sum(p * 2 + 1);
}
ll query(int p, int l, int r) {
if(l <= l(p) && r >= r(p)) return sum(p);
spread(p); //查询也要下传懒标记
ll res = 0;
int mid = l(p) + r(p) >> 1;
if(l <= mid) res += query(p * 2, l, r);
if(r > mid) res += query(p * 2 + 1, l, r);
return res;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
int op, x, y;
ll k;
while(m--) {
scanf("%d%d%d", &op, &x, &y);
if(op == 1) {
scanf("%lld", &k);
change(1, x, y, k);
}
else {
printf("%lld\n", query(1, x, y));
}
}
return 0;
}
【模板】线段树 2
这道题要维护乘和加两个懒标记。
注意:要先乘再加,并且再乘之后 add 的懒标记也要相对改变。
代码:
#include <iostream>
using namespace std;
const int N = 100010;
typedef long long ll;
int n, m, mod;
ll a[N];
struct SegmentTree{
int l, r;
ll sum, add, mul;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
#define add(x) tr[x].add
#define mul(x) tr[x].mul
}tr[N * 4];
int ls(int p) {return p * 2;}
int rs(int p) {return p * 2 + 1;}
void pushup(int p) {sum(p) = (sum(ls(p)) + sum(rs(p))) % mod;}
void build(int p, int l, int r) {
l(p) = l, r(p) = r, mul(p) = 1;
if(l == r) {
sum(p) = a[l] % mod;
return ;
}
int mid = l + r >> 1;
build(ls(p), l, mid);
build(rs(p), mid + 1, r);
pushup(p);
}
void spread(int p) {
sum(ls(p)) = (sum(ls(p)) * mul(p) % mod + (r(ls(p)) - l(ls(p)) + 1) * add(p) % mod) % mod;
sum(rs(p)) = (sum(rs(p)) * mul(p) % mod + (r(rs(p)) - l(rs(p)) + 1) * add(p) % mod) % mod; //更新sum,注意先乘再加
mul(ls(p)) = mul(ls(p)) * mul(p) % mod;
mul(rs(p)) = mul(rs(p)) * mul(p) % mod;
add(ls(p)) = (add(p) + add(ls(p)) * mul(p) % mod) % mod;
add(rs(p)) = (add(p) + add(rs(p)) * mul(p) % mod) % mod; //add 懒标记也要变
mul(p) = 1, add(p) = 0; //消除懒标记
}
void change1(int p, int l, int r, ll val) {
if(l <= l(p) && r >= r(p)) {
sum(p) = sum(p) * val % mod;
mul(p) = mul(p) * val % mod;
add(p) = add(p) * val % mod; //add 懒标记也要改变
return ;
}
spread(p);
int mid = l(p) + r(p) >> 1;
if(l <= mid) change1(ls(p), l, r, val);
if(r > mid) change1(rs(p), l, r, val);
pushup(p);
}
void change2(int p, int l, int r, ll val) {
if(l <= l(p) && r >= r(p)) {
sum(p) = (sum(p) + (r(p) - l(p) + 1) * val % mod) % mod;
add(p) = (add(p) + val) % mod;
return ;
}
spread(p);
int mid = l(p) + r(p) >> 1;
if(l <= mid) change2(ls(p), l, r, val);
if(r > mid) change2(rs(p), l, r, val);
pushup(p);
}
ll query(int p, int l, int r) {
if(l <= l(p) && r >= r(p)) return sum(p);
spread(p);
int mid = l(p) + r(p) >> 1;
ll res = 0;
if(l <= mid) res = (res + query(ls(p), l, r)) % mod;
if(r > mid) res = (res + query(rs(p), l, r)) % mod;
return res;
}
int main() {
scanf("%d%d%d", &n, &m, &mod);
for(int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
int op, x, y;
ll k;
while(m--) {
scanf("%d%d%d", &op, &x, &y);
if(op == 1) {
scanf("%lld", &k);
change1(1, x, y, k);
}
else if(op == 2) {
scanf("%lld", &k);
change2(1, x, y, k);
}
else {
printf("%lld\n", query(1, x, y));
}
}
return 0;
}
P1253 扶苏的问题
要多维护一个覆盖的懒标记。
注意:覆盖某节点时该节点的 add 懒标记要清零(人都没了还更新啥)。
代码:
#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int N = 1000010;
typedef long long ll;
const ll inf = 0x3f3f3f3f3f3f3f3f;
struct SegmentTree{
int l, r;
ll add, cover, maxx;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define maxx(x) tr[x].maxx
#define add(x) tr[x].add
#define cover(x) tr[x].cover
}tr[N * 4];
int n, q;
ll a[N];
int ls(int p) {return p << 1;}
int rs(int p) {return p << 1 | 1;}
void pushup(int p) {maxx(p) = max(maxx(ls(p)), maxx(rs(p)));}
void spread(int p){
if(cover(p) != -inf && l(p) != r(p)){
maxx(ls(p)) = cover(p);
maxx(rs(p)) = cover(p);
cover(ls(p)) = cover(p);
cover(rs(p)) = cover(p);
add(ls(p)) = add(rs(p)) = 0;
cover(p) = -inf;
}
if(add(p) && l(p) != r(p)) {
maxx(ls(p)) += add(p);
maxx(rs(p)) += add(p);
add(ls(p)) += add(p);
add(rs(p)) += add(p);
add(p) = 0;
}
}
void build(int p, int l, int r) {
l(p) = l, r(p) = r, cover(p) = -inf;
if(l == r) {
maxx(p) = a[l];
return ;
}
int mid = l + r >> 1;
build(ls(p), l, mid);
build(rs(p), mid + 1, r);
pushup(p);
}
void change(int p, int l, int r, ll val) {
if(l <= l(p) && r >= r(p)) {
maxx(p) = val;
add(p) = 0;
cover(p) = val;
return ;
}
spread(p);
int mid = l(p) + r(p) >> 1;
if(l <= mid) change(ls(p), l, r, val);
if(r > mid) change(rs(p), l, r, val);
pushup(p);
}
void pluss(int p, int l, int r, ll val) {
if(l <= l(p) && r >= r(p)) {
maxx(p) += val;
add(p) += val;
return ;
}
spread(p);
int mid = l(p) + r(p) >> 1;
if(l <= mid) pluss(ls(p), l, r, val);
if(r > mid) pluss(rs(p), l, r, val);
pushup(p);
}
ll query(int p, int l, int r) {
if(l <= l(p) && r >= r(p)) return maxx(p);
spread(p);
ll res = -inf;
int mid = l(p) + r(p) >> 1;
if(l <= mid) res = max(res, query(ls(p), l, r));
if(r > mid) res = max(res, query(rs(p), l, r));
return res;
}
int main() {
scanf("%d%d", &n, &q);
for(int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
int op, x, y;
ll k;
while(q--) {
scanf("%d%d%d", &op, &x, &y);
if(op == 1) {
scanf("%lld", &k);
change(1, x, y, k);
}
else if(op == 2) {
scanf("%lld", &k);
pluss(1, x, y, k);
}
else {
printf("%lld\n", query(1, x, y));
}
}
return 0;
}
首先区间平均数容易维护,然后区间方差就推一推式子,得到:
然后再维护一个区间平方和就行了。
单点修改 + 区间最大子段和。
因为父节点的和最大的子段可能会跨区间,所以不能直接维护最大子段和,这时候就需要分类讨论最大子段和的取值情况。
-
父节点的最大子段和在左儿子上。
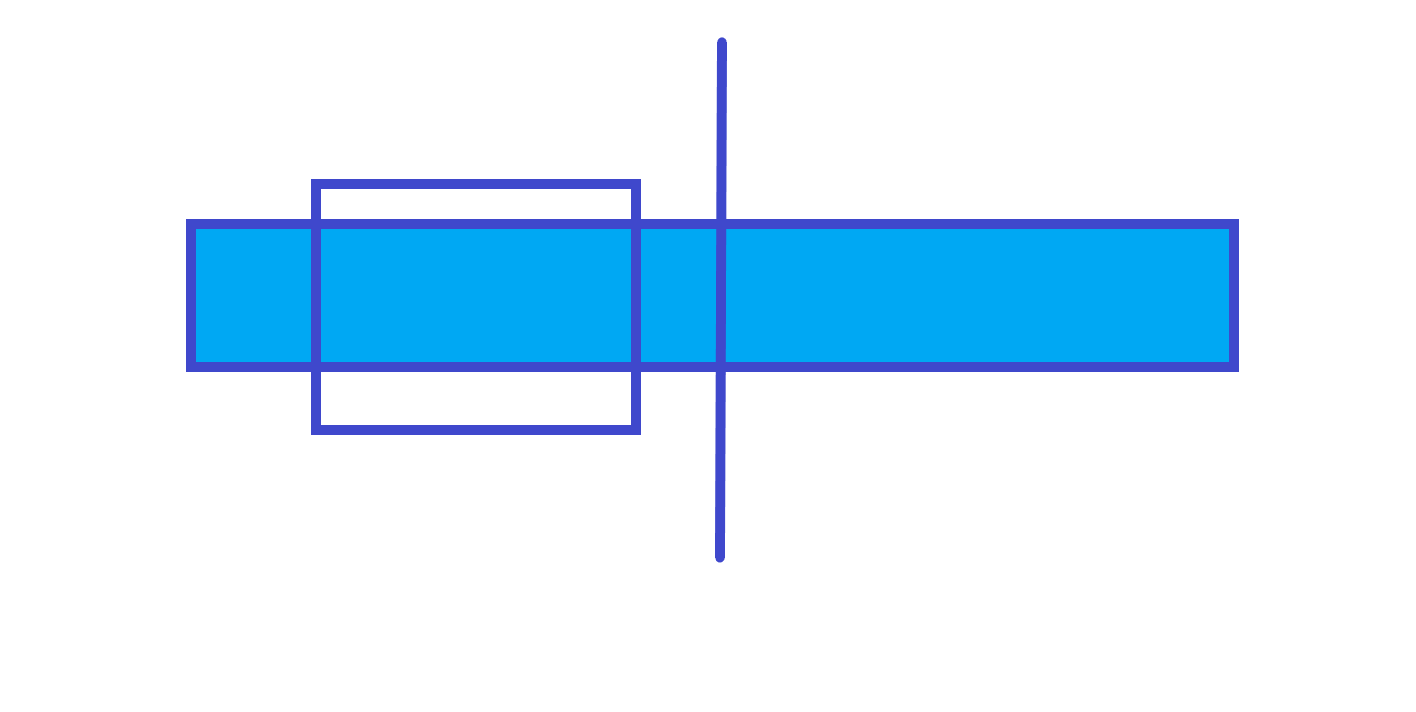
-
父节点的最大子段和在右儿子上。
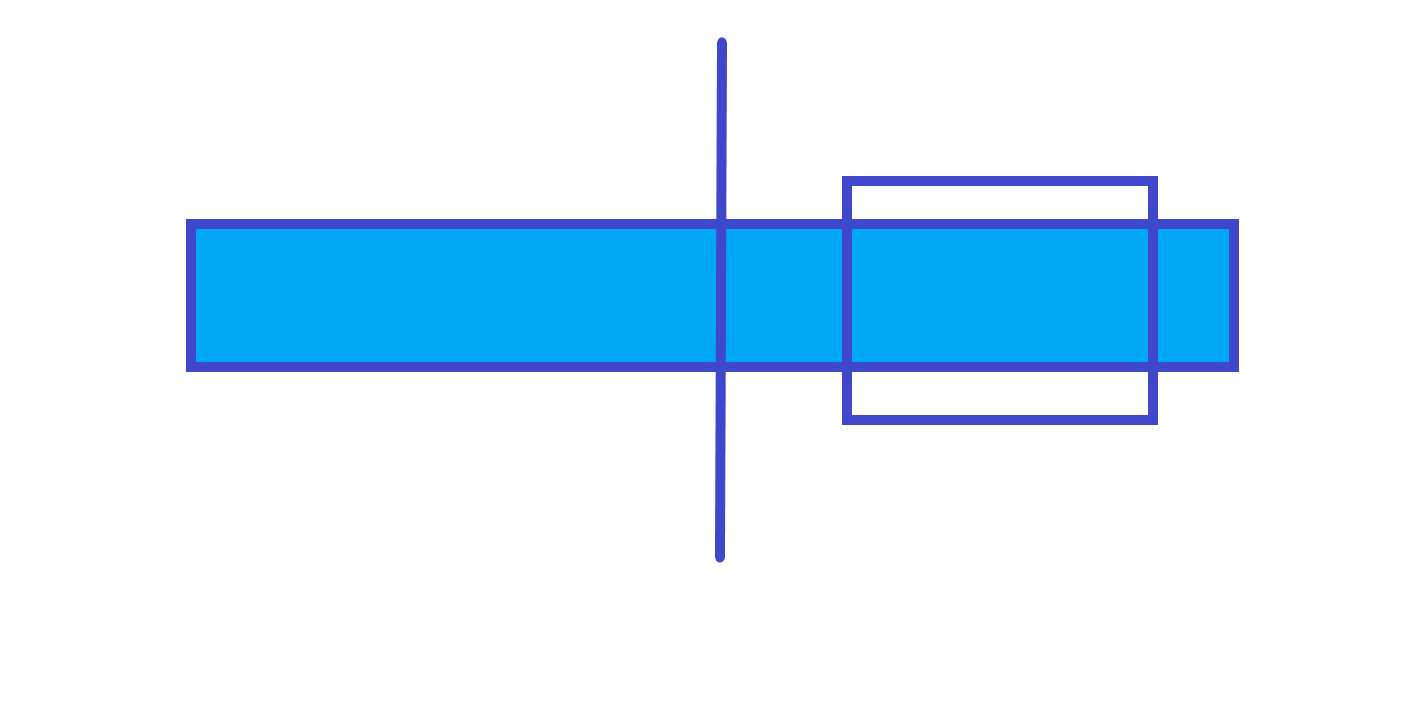
-
跨节点。
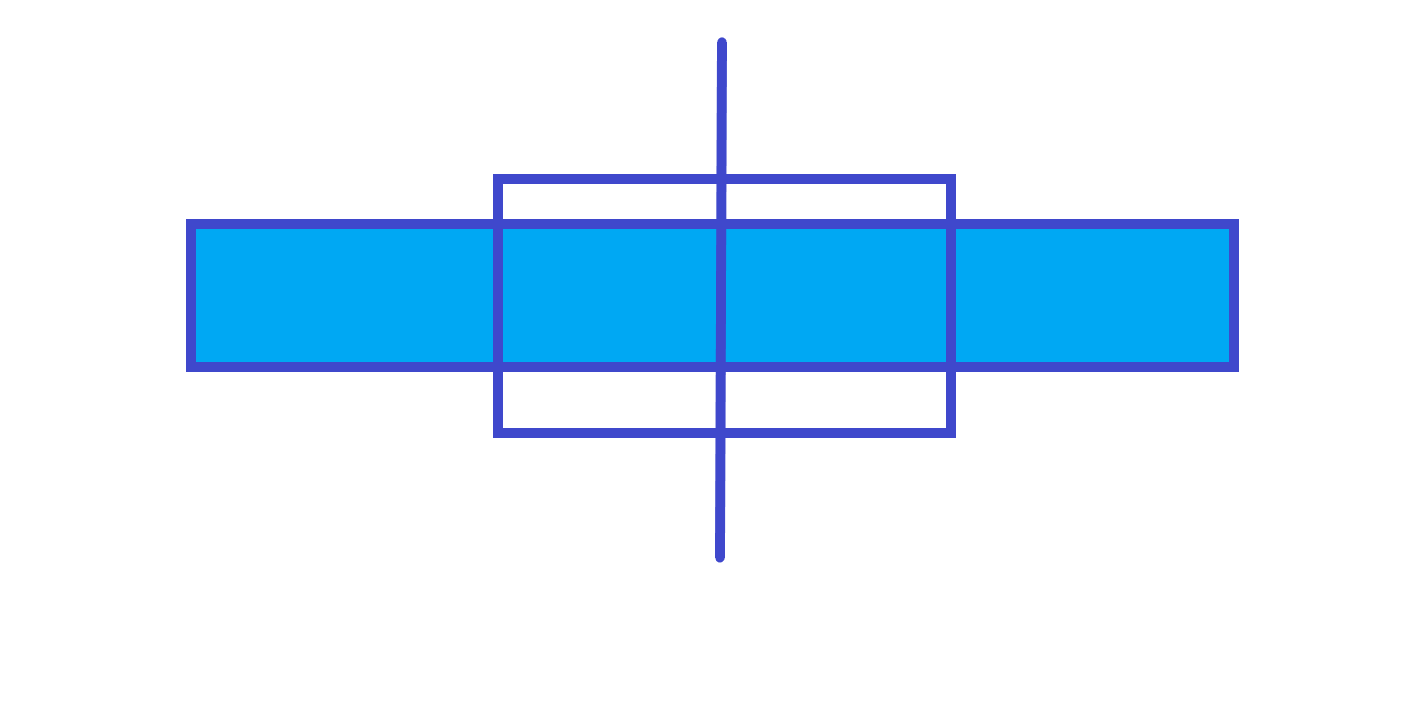
由以上三个图可知,父节点的最大子段和就是左儿子的最大子段和、右儿子的最大子段和和左儿子的最大后缀和 + 左儿子的最大前缀和三个中的最大值,所以我们可以再维护三个值:区间和,区间最大前缀和区间最大后缀。
首先区间和很好维护,那剩下两个怎么办呢?
还是分类讨论取值情况。(以最大前缀为例,最大后缀也是同理)
-
不跨区间
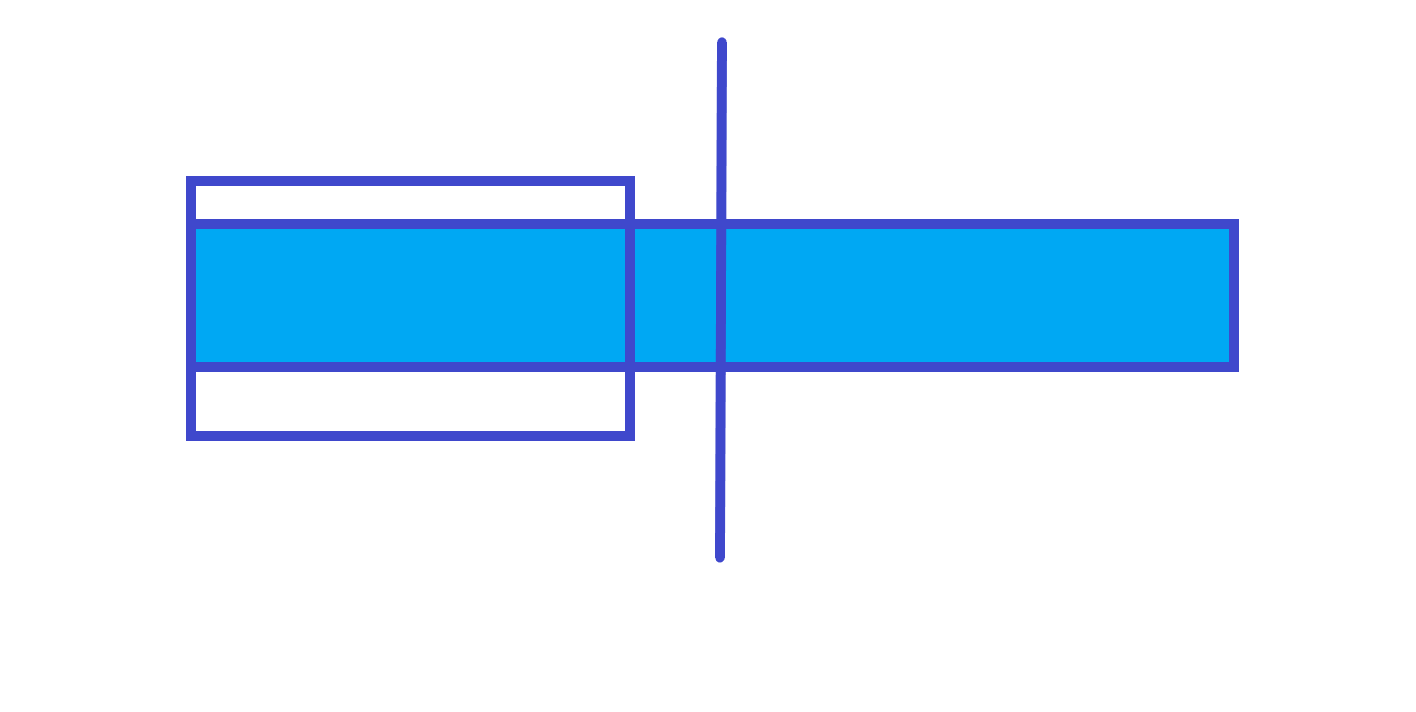
-
跨区间
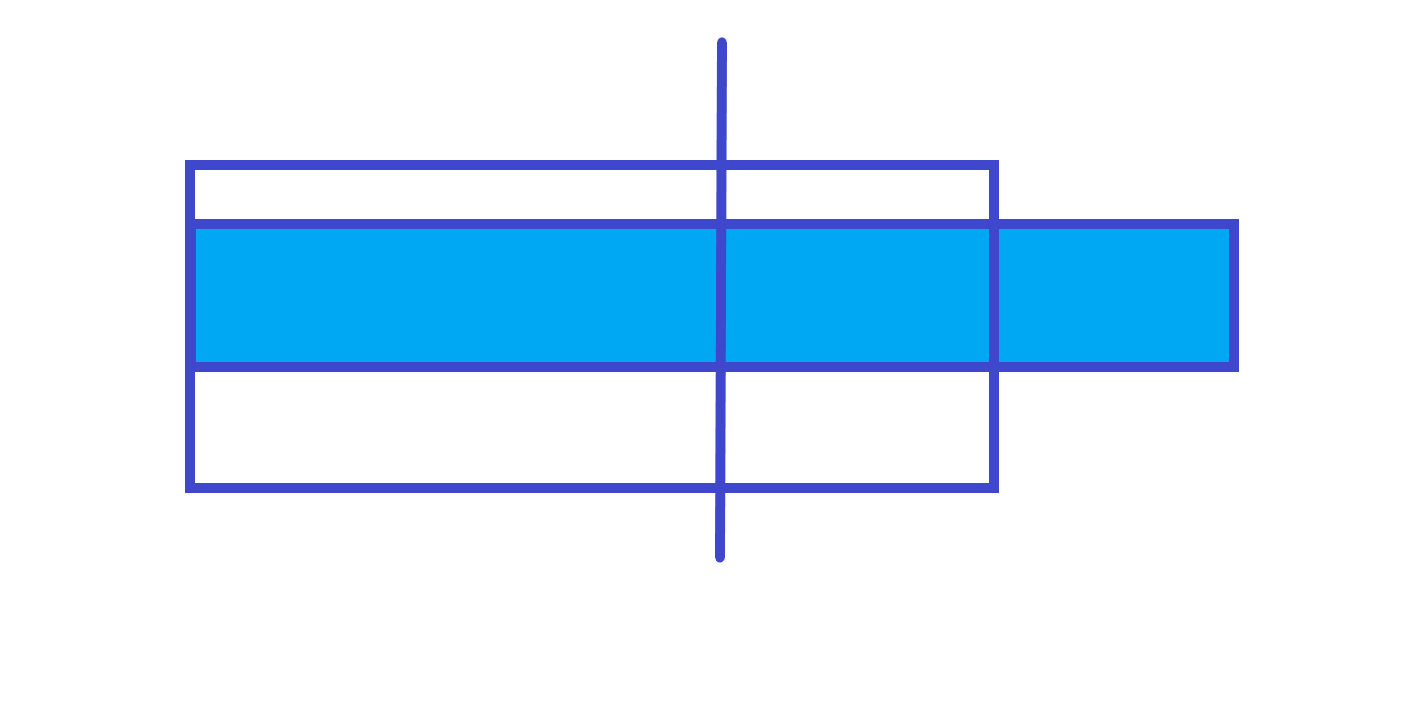
所以最大前缀和就是左儿子的最大前缀和和左儿子区间和 + 右儿子的最大前缀和的最大值。
上线段树模板维护即可。
P2572 [SCOI2010] 序列操作
需要四种操作:区间推平,区间取反,区间求和,区间求最大子段和。
维护一个推平的懒标记和取反的懒标记,注意顺序,在pushdown 时若是推平就把取反覆盖掉,若是取反就把推平反一下。
区间求和好办,区间连续 \(1\) 的个数可以采用类似最大子段和的方式维护。
思路清晰也是可以一遍过的。
P6327 区间加区间 sin 和
合角公式:
推式子:
那么可以维护在线段树中维护区间 \(\sin\) 和和区间 \(\cos\) 和,而且区间 \(\sin\) 和我们已经知道如何维护。
区间 \(\cos\) 和的维护也是同理,推一推式子就出来了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号