图

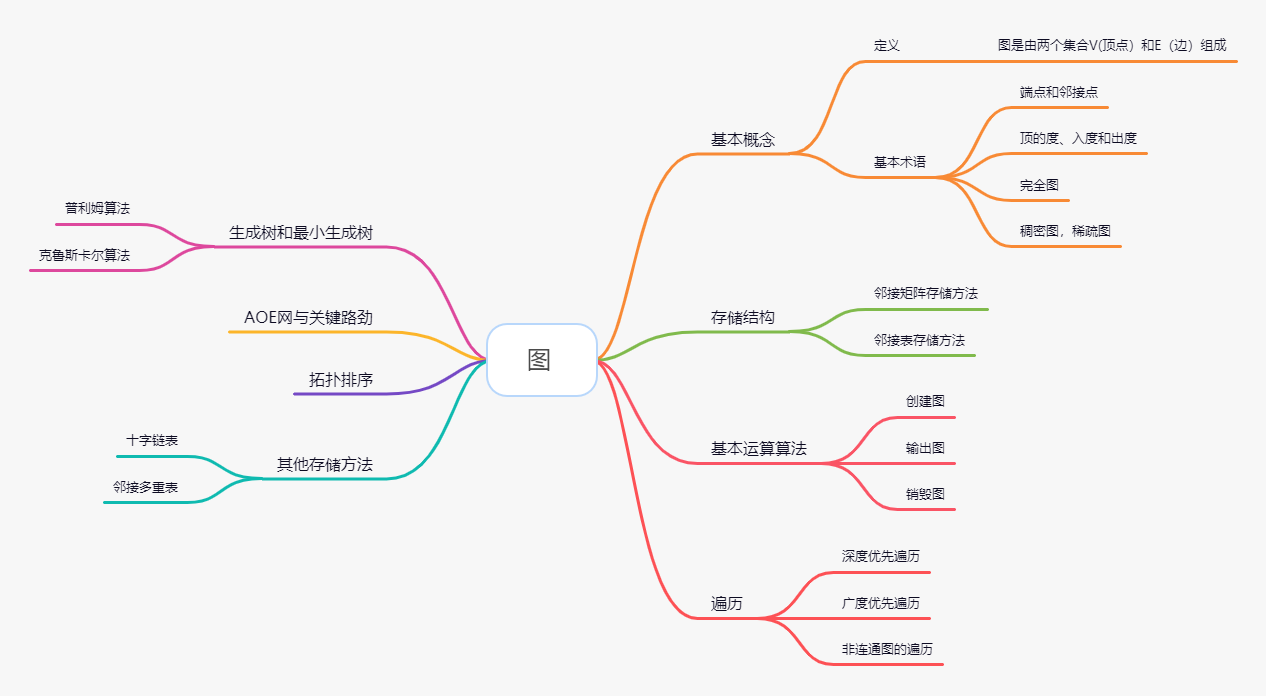
图的思维导图

重要概念

图的定义

图G由两个集合V和E组成，其中V是顶点的有限集合，E是连接V中两个不同顶点的边的有限集合。

邻接表存储方法

图的邻接表是一种顺序和链式相结合的存储方法。

图遍历的概念

从给定图中任意指定的顶点出发，按照某种搜索方式沿着图的边访图所有的顶点，使每个顶点仅被访问一次。

图的基本术语

端点和邻接点

顶的度，入度和出度

完全图

稠密图，稀疏图

子图

路径和路径长度

回路和环

连同，连通图和连同分量

图的基本算法

创建图

void CreateAdj(AdjGraph*& G, int A[MAXV][MAXV], int n, inte) // 创建图的邻控主
{
	G = (AdjGraph*)malloc(sizeof(AdjGraph));
	for (i = 0; i < n; i++)
		G->adjlist[i].firstarc = NULL;//给邻接表中所有头结点的指针城置打值
	for (i = 0; i < n; i++)//检查邻接矩阵中的每个元素
		G->adjlist[i].firstarc = NULL;
	for (j = n - 1; j >= 0; j - --)//检查邻接矩阵中的每个元素
		for (i = 0; i < n; i++)
			if (A [[]!= 0 && A[iG] != INF)//存在一条边
			{
				p = (ArcNode*)malloc(sizeof(ArcNode));//创建一个结点p
				p->adjvex = j;//存放邻接点
				p->weight = A[i][];//存放权
				p->nextarc = G->adjlist[i].firstarc;//采用头插法插人结点p
				G->adjlist[i].firstarc = p;
			}
	G->n = n; G->e = e;
}

 输出图

void DispAdj(AdjGraph* G) {//输出邻接表G
    int i;
    ArcNode* p;
    for (i = 0; i < G->n; i++) {
        p = G->adjlist[i].firstarc;
        printf("%3d: ", i);
        while (p != NULL) {
            printf("%3d[%d->", p->adjvex, p->weight);
            p = p->nextarc;
        }
        printf("^\n");
    }
}

销毁图

void DestroyAdj(AdjGraph*& G) {//销毁邻接表
    int i;
    ArcNode* pre, * p;
    for (i = 0; i < G->n; i++) {//扫描所有的单链表
        pre = G->adjlist[i].firstarc;//p指向第i个单链表的头结点
        if (pre != NULL) {
            p = pre->nextarc;
            while (p != NULL) {
                free(pre);//释放第i个单链表的所有边结点
                pre = p; p = p->nextarc;
            }
            free(pre);
        }
    }
    free(G);//释放头结点数组
}

广度优先遍历

void BFS(AdjGraph* G, int v) {
    int w, i; AdjNode* p;
    SqQueue* qu;//定义环形队列指针
    InitQueue(qu);//初始化队列
    int visited[MAXV];//定义顶点访问标记数组
    for (i = 0; i < G->n; i++) //访问标记数组初始化
        printf("%2d", v);//输出访问标记数组
    visited[v] = 1;//置已访问标记
    enQueue(qu, v);
    while (!QueueEmpty(qu)) {//队列不空循环
        deQueue(qu, w);//出队一个顶点w
        p = G->adjlist[w].firstarc;//指向w的第一个邻接点
        while (p != NULL) {//查找w的所有邻接点
            if (visited[p->adjvex] == 0) {//若当前邻接点未被访问
                printf("%2d", p->adjvex);
                visited[p->adjvex] = 1;//置已访问标记
                enQueue(qu, p->adjvex);//该顶点入队
            }
            p = p->nextarc;//查找下一个邻接点
        }
    }
    printf("\n");
}

生成树的概念

一个连同图的生成树是一个极小连通图，其中含有图中的全部顶点，和构成一棵树的（n-1）条边。

疑难问题

克鲁斯卡尔算法

AOE网与关键路径