忘光了,所以复习【POL】
拉格朗日插值
给定 \(n\) 个点 \(P_i(X_i,Y_i)\) ,求过这 \(n\) 个点的唯一一个多项式。
朴素拉格朗日插值
只求 \(f(k)\)。
作 \(Q_i(X_i,0)\),是 \(P_i\) 在 \(x\) 轴上的投影。
所以,如果构造了 \(n\) 个多项式 \(g_i(1\le i\le n)\),使得 \(g_i\) 过 \(P_i\) 和 \(Q_j(j\neq i)\),那么 $\displaystyle f=\sum\limits_{i=1}^n g_i $ 就是答案。
接下来构造:\(\displaystyle g_i=Y_i\prod\limits_{j\neq i}\dfrac{x-X_j}{X_i-X_j}\),使得对于 \(j\neq i\) 有 \(g_i(X_j)=0\),\(j=i\) 恰好 \(g_i(X_i)=Y_i\)。
所以:
这样就可以 \(O(n^2)\) 快速求 \(f(k)\) 了。
带入即可。
坐标连续时的拉格朗日插值
\(X_i=i\),只求 \(f(k)\)。
代入得 \(\displaystyle f=\sum_{i=1}^n Y_i\prod_{j\neq i}\dfrac{x-j}{i-j}\)
仔细观察一下,可以发现,我们只要预处理前后缀 \(\displaystyle\prod_j x-j\) 即可。
所以:
就可以 \(O(n)\) 了。
设答案为一个 \(k+1\) 次多项式 \(\displaystyle f(x)=\sum_{i=0}^{k+1}a_i x^i\)。
直接带入前 \(k+2\) 个点,然后用坐标连续时的拉格朗日插值即可。
重心拉格朗日插值
支持动态加点。
考虑:
然后维护 \(\displaystyle a=\prod_{d=1}^n (x-X_d)\),\(b_i=\dfrac{Y_i}{\prod_{j\neq i}(X_i-X_j)}\)。
可以做到 \(O(n)\) 修改,\(O(n)\) 查询。
求出多项式每一项的系数
提出系数,那么 \(\displaystyle f=\sum_{i=1}^n Y_i\left(\prod_{j\neq i}\dfrac{1}{X_i-X_j}\right)\dfrac{\prod_{j=1}^n (x-X_j)}{x-X_i}\)
所以预处理时先暴力卷出 \(\displaystyle\prod_{j=1}^n (x-X_j)\),再每个地方暴力除以 \(x-X_i\),最后乘上系数。
复杂度 \(O(n^2)\)
然后我就写了一个程序得出了以下著名函数:
\(f(x)=\dfrac{114509}{24}x^4-\dfrac{572545}{12}x^3+\dfrac{4007815}{24}x^2-\dfrac{2862713}{12}x+114509\)
\(\displaystyle f(x)=\dfrac{28627}{30}x^5-\dfrac{28627}{2}x^4+\dfrac{486659}{6}x^3-\dfrac{429405}{2}x^2+\dfrac{3921914}{15}x-114508\)
多项式乘法
快速傅里叶变换(FFT)
快速卷积。
离散傅里叶变换(DFT)
DFT,把一个多项式从系数表示法转化为点值表示法。
为什么要转成点值表示法呢?
考虑两个多项式乘起来,只要装换成点值,然后把点值相乘即可。
单位根
设两个多项式次数分别为 \(n,m\)。
大多数想法是取任意 \(n+m+1\) 个点(因为答案是 \(n+m\) 次),但是可能 TLE。
所以考虑一些特殊点。
这时候就要取到单位根了。\(n\) 次单位根记作 \(\large\omega_n\),即为 \(x^n=1\) 的所有复数解。
一共有 \(n\) 个单位根,所以记作 \(\large\omega_n^0,\omega_n^1,\dots,\omega_{n}^{n-1}\),并且以幅角大小排序。
在复数域中只有以 \(O\) 为圆心半径为 \(1\) 的圆上的点才有可能是单位根。
性质
对于上标 \(\ge n\) 或 \(<0\) 的情况,可认为上标在模 \(n\) 意义下,即 \(\large\omega_n^k=\omega_n^{k\bmod n}\)。
-
\(\large\omega_n^0=1\)
定有一个根 \(1\)。
-
\(\large\omega_n^k=(\omega_n^1)^k\)
考虑乘上一个 \(\large\omega_n^1\) 表示把当前向量转一个 \(\frac1n\) 的圆周。
-
\(\large\left(\omega_{n}^j\right)^k=\omega_n^{jk}\)
由上一条简单得出。
-
\(\large\omega_n^j\omega_n^k=\omega_n^{j+k}\)
考虑 \(\large(\omega_n^1)^j(\omega_n^1)^k=(\omega_n^1)^{j+k}=\omega_n^{j+k}\)。
-
\(\large\omega_{2n}^{2k}=\omega_n^k\)
仔细想一想就知道是对的,并且 \(\large\omega_{pn}^{pk}=\omega_n^k\)。
-
对于一个偶数 \(n\),有 \(\large \omega_n^{(k+\frac{n}{2})}=-\omega_n^k\)
\(\large \omega_n^{(k+\frac n2)}=\omega_n^k \omega_{n}^\frac n2\)
把 \(\large\omega_n^\frac n2\) 看做旋转 \(\frac12\) 圈即可。
求单位根
首先 \(\omega_n^0(1,0)\),然后三角函数随便算就可以知道 \(\displaystyle \omega_{n}^1(\cos\frac{2\pi}{n},\sin\frac{2\pi}n)\)。
考虑 \(\large\omega_n^1\) 表示旋转 \(\frac1n\) 圆周。那么 \(\large\omega_n^i=\omega_n^{i-1}\omega_n^1\)。
快速傅里叶变换(FFT)
考虑一个多项式 \(\displaystyle f(x)=\sum_{i=0}^{n-1} a_ix^i\),把它按次数奇偶性分为两部分。
此部分设 \(m=\frac n2\)。
即:
这里需要保证 \(n=2^p(p\in\mathbb{n})\),这样保证不会出现除尽的情况,如果 \(n\) 不能表示为 \(2^p\),那就高位补 \(0\),以下设 。
然后设:
则:
代入单位根:
-
代入 \(\large{\omega_n^k}\)\((k<m)\):
\[\large\begin{aligned} f(\omega_n^k)&=f_0\left((\omega_n^k)^2\right)+\omega_n^kf_1\left((\omega_n^k)^2\right)\\ &=f_0(\omega_m^k)+\omega_n^kf_1(\omega_m^k) \end{aligned} \] -
代入 \(\large{\omega_n^{k+m}}\)\((k<m)\):
我们把二者对比一下:之差了一个符号!这时候就开始体会到单位根的牛了。
在这个时候,如果我们知道了 \(\large\omega_m^k\)\((k<m)\) 在 \(f_0,f_1\) 下的点值,我们就可以 \(O(n)\) 推出 \(\large\omega_n^k\)\((k<n)\) 在 \(f\) 下的点值。
那么我们就可以递归求出所有点值,不难发现递归共 \(\log n\) 层。
所以复杂度为 \(O(n\log n)\)。
快速傅里叶逆变换(IFFT)
首先有一个结论:
证明:
首先有:
讨论:
-
\(j=k\)
\(\omega_n^0=1\),所以 \(f(k)\) 一共有 \(n\) 次被计算到,答案为 \(nf(k)\)。
-
\(j\neq k\)
设 \(p=j-k\),所以贡献为 \(\displaystyle \sum_{i=0}^{n-1}\omega_n^{ip}f(k+p)=\omega_n^pf(k+p)\sum_{i=0}^{n-1}\omega_n^{i}\)
可以发现后面有个等比数列求和:\(\displaystyle\sum_{i=0}^{n-1}\omega_n^{i}=\frac{\omega_n^n-\omega_n^0}{\omega_n^1-1}=0\)
所以就证完了。
可以发现根据这个式子,我们只要改变一下单位根的旋转方向(把旋转一个单元变为 \(\omega_n^{-1}\)),并且在最后除以一个 \(n\),就变成了 FFT。
具体的,只要改变单位根里的一个符号即可。
代码
代码(处理单位根):
inline void init(Ci N,const bool op){
o.resize(max(N,2));
o[0]={1,0};o[1]={cos(PI/N),(op?1:-1)*sin(PI/N)};
for(int i=2;i<N;i++)o[i]=o[i-1]*o[1];
}
代码(FFT):
void fft(vector<Cp>&f,Ci n,const bool op){
if(n==1)return;
vector<Cp>f0,f1;int m=n>>1;
f0.resize(m);f1.resize(m);
for(int i=0;i<m;i++)f0[i]=f[i<<1],f1[i]=f[i<<1|1];
fft(f0,m,op);fft(f1,m,op);
init(m,op);
for(int i=0;i<m;i++){
f[i]=f0[i]+o[t][i]*f1[i];
f[i+m]=f0[i]-o[t][i]*f1[i];
}
}
代码(多项式乘法):
inline void fft(){fft(x,x.size(),1);}
inline void Ifft(){fft(x,x.size(),0);}
inline friend Poly operator*(Poly U,Poly V){
int S=U.size()+V.size()-1;
int u=1;while(u<S)u<<=1;
U.resize(u);V.resize(u);
U.fft();V.fft();
for(int i=0;i<u;i++)U[i]*=V[i];
U.Ifft();
for(int i=0;i<u;i++)U[i].x/=u;
return U;
}
蝴蝶变换
我们的递归版是递归到最下面然后合并上来。
我们直接到最下面然后直接合并。
考虑按奇偶性分组的本质是按当前二进制位向左或向右,正好与原标号二进制相反,所以最后一层的标号即为位置序号的翻转。
感觉不太说的清楚,看图:
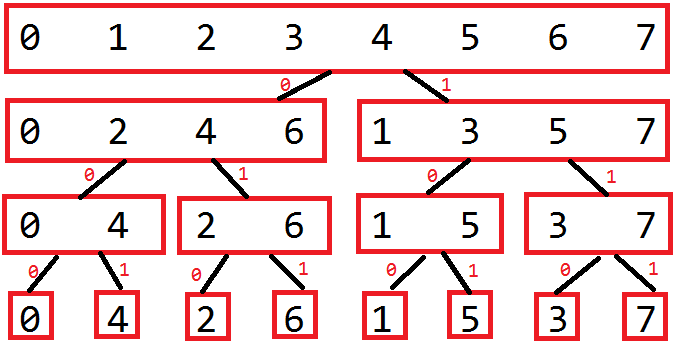
比如上图中第 \(4\) 个位置标号为 \((011)_{(2)}\),填的数是 \((110)_{(2)}\),即 \(6\)。
接下来,如何快速翻转二进制呢?
设翻转后的数组为 \(r\),那么 \(\displaystyle r_i=\frac{r_{\lfloor\frac i2\rfloor}}{2}+[i\bmod 2=1]2^{S-1}\)。
\(S\) 为 \(r\) 的长度,\(2^{S-1}\) 即为最高位。
把二进制串 \(\overline{a_1a_2\dots a_n}\) 除以 \(2\), \(\overline{0a_1\dots a_{n-1}}\),翻转后 \(\overline{a_na_{n-1}\dots a_1}\),变为 \(\overline{a_{n-1}a_{n-2}\dots a_10}\)。
可以发现只要删去最后一位,再加个最高位就行了。
代码(迭代 FFT):
for(int l=2,t=1;l<=n;l<<=1,t++)
for(vector<Cp>::iterator i=f.begin();i!=f.end();i+=l){
int m=l>>1;
for(int j=0;j<m;j++){
Cp tmp=o[(n>>t)*j]*i[j+m];
i[j+m]=i[j]-tmp;i[j]+=tmp;
}
}
给出 \(n\) 个数 \(q_1,q_2, \dots q_n\),定义
\[F_j=\sum_{i = 1}^{j - 1} \frac{q_i \times q_j}{(i - j)^2}~-~\sum_{i = j + 1}^{n} \frac{q_i \times q_j}{(i - j)^2}\\ \]\[E_i~=~\frac{F_i}{q_i} \]对 \(1 \leq i \leq n\),求 \(E_i\) 的值。\(1 \leq n \leq 10^5\),\(0 < q_i < 10^9\)。
这个东西其实是一个普通卷积和一个减法卷积,分别算即可。
快速数论变换(NTT)
NTT
由于 FFT 需要用到单位根,不可避免的就会有精度误差,而且也有较大的常数,数学家们已经证明,在复数域中,单位根是唯一一类满足要求的数。
不过 OI 中不少题在模意义下,所以我们考虑同余系中的原根。
对于模数 \(p\),有一个原根 \(g\)。
可以构造在模意义下满足单位根性质的 \(\large\omega_n^k=g^{\frac{(p-1)k}n}\)
不难发现需要满足 \(n|(p-1)\),而著名模数 \(998244353=2^{23}\times7\times17+1\)。
这在 \(n=2^k\) 时基本可以用。
任意模数NTT
用 3 个 NTT 模数,最后 CRT 合并即可。
分治 FFT/NTT
考虑 \(n\) 个二项多项式卷起来或者一个多项式自己对自己的递推式,可以用分治做到 \(O(n\log^2 n)\)。
关于递推的分治方法就是每次算左半边对右半边的贡献。
多项式求逆
由于 \(k\ge n\) 时,\(f(x)\) 在模 \(x^k\) 意义下的逆元等于其在模 \(x^n\) 意义下的,所以我们可以把模 \(x^n\) 补为模 \(x^k\)。
设 \(s=2^u,t=2^{u-1}\)。
设 \(f\) 在模 \(x^t\) 意义下的逆元为 \(G\),在模 \(x^s\) 意义下的为 \(g\),考虑从 \(G\) 推到 \(g\)。
首先有:
所以就可以递推了。
复杂度 \(T(n)=T(\frac n2)+O(n\log n)=O(n\log n)\)。
多项式带余除法
求 \(q(x),r(x)\) 满足 \(f(x)=q(x)g(x)+r(x)\)
设 \(f\) 的次数为 \(n\),\(g\) 的次数为 \(m\)。
把 \(x\) 变成 \(\frac1x\)
设 \(f_r(x)=x^{d_f}f(x^{-1})\) ,\(d_f\) 表示多项式 \(f\) 的次数,其实不难发现 \(f_r(x)\) 就是 \(f(x)\) 的系数 reverse 一下。
可以发现用一下求逆即可。
多项式对数函数(ln)
求 \(g(x)\) 满足 \(g(x)\equiv\ln f(x)\pmod{x^n}\)
导数和积分都可以直接来。
多项式指数函数(exp)
求 \(g(x)\) 满足 \(g(x)\equiv e^{f(x)}\pmod{x^n}\)
牛顿迭代
不难发现上面的方法做不了。
引入牛顿迭代的问题:
求 \(g(x)\) 满足 \(f(g(x))\equiv 0\pmod{x^n}\)
考虑求逆的递推思路,设 \(s=2^u,t=2^{u-1}\)。
假设当前求出了 \(f(G(x))\equiv 0\pmod{x^t}\)。
将 \(f(g(x))\) 在 \(G(x)\) 处泰勒展开:
可以发现,\(g\) 和 \(G\) 在 \(\bmod x^t\) 的意义下是一样的。
所以 \(g(x)-G(x)\) 只剩下 \(x^t\) 及以上次项,所以 \(i\ge 2\) 时,\((g(x)-G(x))^i\) 的最低非 \(0\) 位在 \(s\) 以上,\(\bmod x^s\equiv 0\)。
复杂度同求逆:\(O(n\log n)\)
exp
设 \(F(g(x))=\ln g(x)-f(x)\),然后直接带入牛迭的式子:
然后就可以递推了。
多项式快速幂
求 \(g(x)\) 满足 \(g(x)\equiv f^C(x)\pmod{x^n}\)。
然后就是 exp。
多项式开根
求 \(g(x)\) 满足 \(g^C(x)\equiv f(x)\pmod{x^n}\)。
设 \(F(g(x))=g^C(x)-f(x)\),然后直接带入牛迭的式子:
多项式快速幂。
多项式多点求值
给定 \(n\),长度为 $n $ 的多项式 \(f\) 以及数组 \(a\),求所有 \(f(a_i)\)。
分治。
设 \(t=\lfloor\frac m2\rfloor\)
可以发现,对于 \(1\le i\le t\),\(f(i)=0A(i)+B(i)=B(i)\),对于 \(t+1\le i\le m\),\(f(i)=0C(i)+D(i)\)。
然后发现我们可以分治 NTT 预处理 \(g,h\),所以递归时做一遍多项式取模即可,但常数巨大。
多项式快速插值
拉插的式子:
发现后面 \(Y_i\) 是一个常数,下面可以看做:
可以洛必达
所以分治 NTT 后多点求值。
设 \(f_{l,r}\) 表示 \([l,r]\) 的答案。
GL&HF
目前就这些,有问题请指出,之后可能会再施工。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号