拓扑学基础

拓扑学基础

1. 拓扑空间 \((X, \mathcal{T})\)：\(\varnothing, X\in \mathcal{T}\subseteq\mathcal{P}(X)\) 且对任意并、有限交封闭

2. \(x\) 的邻域系 \(\mathcal{U}(x)\)：以包含 \(x\) 的某个开集为子集的集合全体

3. 子集 \(A\) 的点 \(x\) 的分类（依赖拓扑及全空间的选取）

   • 内点（内部 \(A^\circ\)）：\(x\in X,A\in\mathcal{U}(x)\)
   • 边界点（边界 \(A^b\)）：\(x\not\in A^e\) 且 \(x\not\in A^\circ\)
   • 外点（外部 \(A^e\)）：\(A\) 的补集 \(A^c\) 的内点
   • 接触点（闭包 \(\overline{A}\)）：对任意 \(U\in\mathcal{U}(x)\)，恒有 \(U\bigcap A\neq\varnothing\iff A\) 中有网收敛到 \(x\)
   • 极限点（聚点，导集 \(A^{\prime}\)）：对任意 \(U\in\mathcal{U}(x)\)，恒有 \(U\bigcap \big(A\setminus\{x\}\big)\neq\varnothing\)
     • ω 聚点：含有 \(x\) 的任一开集必含有 \(A\) 的无穷多个点
       • 凝聚点：含有 \(x\) 的任一开集必含有 \(A\) 中不可数个点
   • 孤立点（\(A^i\)）：\(x\in A\) 且存在 \(V\in\mathcal{A}(x)\)，使得 \(V\bigcap A=\{x\}\)
   • \(X=\overline{A} \cup A^e, \overline{A}=A^b\cup A^\circ=A^\prime\cup A^i\)
   • \(A^\prime\) 恒为闭集 \(\iff \{x\}^\prime\) 恒为闭集

4. 子集 \(A\) 的性质（依赖拓扑及全空间的选取）

   • 闭集：某个开集的补集 \(\iff A^{\prime}\subset A\iff A=\overline{A}\)
   • 完备集：\(A=A^{\prime}\)
   • \(A\) 在 \(B\) 中稠密：\(B\subset\overline{A}\)
   • \(A\) 在 \(X\) 中无处稠密：\((\overline{A})^\circ=\varnothing\)
   • 第一纲集：可数个无处稠密集的并集
   • 第二纲集：非第一纲集
     • Baire 空间：\(X\) 的任意非空开集都是 \(X\) 的第二纲集
   • \(G_\delta\) 集：可以表示为可数个开集的交
   • \(F_\sigma\) 集：可以表示为可数个闭集的并
     • \(A\) 是 \(X\) 的 \(G_\delta\) 集 \(\iff X\setminus A\) 是 \(X\) 的 \(F_\sigma\) 集

5. 映射 \(f:(X, \mathcal{T})\to (Y, \mathcal{Y})\) 的性质

   • 单射：任意两个不同的点有不同的像
   • 满射：\(Y\) 内每一点必是 \(X\) 内某一点的像
   • 连续映射：开集的原像是开集 \(\iff\) 闭集的原象是闭集 \(\iff\) 拓扑（子）基的原象是开集
   • 同胚映射：连续双射且逆映射连续 \(\iff\) 连续双射 + 开 \(\iff\) 连续双射 + 闭
   • 开映射：开集的原像是开集
   • 闭映射：闭集的原像是闭集
   • 序列连续映射：对任意 \(x_n\to x\)，必有 \(f(x_n)\to f(x)\)

6. 拓扑空间的生成：拓扑子基 \(\mathcal{V}\overset{有限交}{\longrightarrow}\) 拓扑基 \(\mathcal{B}\overset{任意并}{\longrightarrow}\) 拓扑 \(\mathcal{T}\)

   • \(x\) 的邻域基 \(\mathcal{N}_x\)：\(\forall U\in \mathcal{U} _x, \exists V\in \mathcal{N}_x,\quad \text{s.t.}\quad x\in V\subset U\)
   • 若 \(\mathcal{B}\) 是 \(X\) 的拓扑基，则 \(\mathcal{B}_x:=\{B\in\mathcal{B}|x\in B\}\) 是 \(x\) 的邻域基。
   • 如果一个集族 \(\mathcal{B}\) 满足：（1）：\(X=\displaystyle\bigcup_{B\in\mathcal{B}} B\)；（2）：\(\forall B_1, B_2\in \mathcal{B} , x\in B_1\cap B_2, \exists B\in \mathcal{B} \ \text{s.t.}\ x\in B\subset B_1\cap B_2\)，那么存在唯一的拓扑以 \(\mathcal{B}\) 为基。

7. 非空集 \(A\) 上的二元关系 \(\preccurlyeq\)

   • 预序集 \((A, \preccurlyeq)\)：1 + 2
   • 定向集 \((A, \preccurlyeq)\)：1 + 2 + 3
   • 偏序集 \((A, \preccurlyeq)\)：1 + 2 + 4
   • 全序集 \((A, \preccurlyeq)\)：1 + 2 + 4 + 5
   1. 自反：\((\forall a\in A)\quad a\preccurlyeq a\)
   2. 传递：\((\forall a\in A)(\forall b\in A)(\forall c\in A)\quad[a\preccurlyeq b, b\preccurlyeq c]\implies a\preccurlyeq c\)
   3. 公共大元：\((\forall a\in A)(\forall b\in A)(\exists c\in A)\quad a\preccurlyeq c \text{ 且 } b\preccurlyeq c\)
   4. 反对称：\((\forall a\in A)(\forall b\in A)\quad[a\preccurlyeq b, b\preccurlyeq a]\implies a=b\)
   5. 两两可比较：\((\forall a\in A)(\forall b\in A)\quad a\preccurlyeq b\text{ 或 }b\preccurlyeq a\)

8. 收敛性

   • 集 \(X\) 中的网 \((x_a)_{a\in A}\)（广义序列） ：定向集 \((A, \preccurlyeq)\) 到集 \(X\) 的映射
   • 集 \(X\) 中的序列 \((x_n)_{n\in \mathbb{N}}\)：定向集 \((A, \preccurlyeq)\) 取 \((\mathbb{N}, \leqslant)\) 的网
     • \([-\infty,+\infty]\) 中网 \((x_a)_{a\in A}\) 的上 / 下极限（limit superior/inferior）
       • \(\overline{\lim} \ x_a=\limsup x_a=\displaystyle \inf_{a\in A}\displaystyle\sup_{b\in A, a\preccurlyeq b}x_b\)
       • \(\underline{\lim}\ x_a=\liminf x_a=\displaystyle\sup_{a\in A}\inf_{b\in A, a\preccurlyeq b}x_b\)
     • 网 \((x_a)_{a\in A}\) 的极限点（\(x\in \operatorname{lim}x_a\)）：任给 \(U\in \mathcal{U}(x), x_a\) 终在 \(U\) 中
       • \((\exists c\in A)(\forall a\in A)\quad a\succcurlyeq c\implies x_a\in U\)
     • 网 \((x_a)_{a\in A}\) 的\(\textcolor{blue}{聚点}\)（\(x\in \operatorname{clust}x_a\)）：\((x_a)_{a\in A}\) 有\(\textcolor{blue}{子网}\)收敛到 \(x\iff\) 任给 \(U\in \mathcal{U}(x), x_a\) 常在 \(U\) 中
       • \((\forall c\in A)(\exists a\in A)\quad a\succcurlyeq c\text{ 且 } x_a\in U\)
     • 网 \((x_a)_{a\in A}\) 的\(\textcolor{blue}{序列聚点}\)（\(x\in \operatorname{sclust}x_a\)）：\((x_a)_{a\in A}\) 有\(\textcolor{blue}{子序列}\)收敛到 \(x\)
     • 网 \((x_a)_{a\in A}\) 的子网 \((x_{k_b})_{b\in B}\)：\((\forall a\in A)(\exists d\in B)(\forall b\in B)\quad b\succcurlyeq d\implies k_b\succcurlyeq a\)
     • 序列 \((x_n)_{n\in \mathbb{N}}\) 的子序列 \((x_{k(n)})_{n\in \mathbb{N}}\)：\(k:\mathbb{N}\to \mathbb{N}\) 严格单增
     • 超网（ultranet）：任给 \(X\) 的子集 \(A, x_a\) 要么终在 \(A\)，要么终在 \(A\) 的补集 \(X\setminus A\)（该定义不依赖拓扑）
       • 超网的子网是超网
       • 超网的每个聚点都是极限点
       • 任意网均有子网是超网
     • 序列的子网不一定是子序列（\(k\) 可以有多条单增的强制链）
   • \(x\in\overline{A}\iff\) 存在 \(A\) 中的网收敛于 \(x\)
     • 网的收敛能完全描述闭包算子，因此能完全描述 \(X\) 的拓扑结构
   • \(\operatorname{sclust}x_a\subset\operatorname{clust}x_a\subset\overline{\{x_a\}_{a\in A}}\)
     • 网【序列】的元素有无穷【可数】序，但构成的集合可能为有限集
   • 乘积空间中网的收敛为按分量收敛

9. 拓扑空间 \((X,\mathcal{T})\) 的子集 \(U\) 称为 \((X,\mathcal{T})\) 的序列开集，若任给 X 的序列 \(\{x_n\}\)，只要 \(\{x_n\}\) 收敛于 \(x\in U\)，则 \(\{x_n\}\) 终在 \(U\) 中；

   • \(X\) 的全体序列开集 \(s(\mathcal{T})\) 构成 \(X\) 上的一个比 \(\mathcal{T}\) 细的拓扑
   • 拓扑空间 \((X,\mathcal{T})\) 称为序列空间 \((SS)\)，若 \(\mathcal{T}=s(\mathcal{T})\)，即 \((X,\mathcal{T})\) 的序列开集都是开集
   • 序列闭集：集合中任意收敛序列的极限点（序列闭包）都在该集合中
   • \(C_1\implies SS\)
   • 序列空间中网性质均可以用序列性质代替，如网的序列聚点，序列（下半）连续等

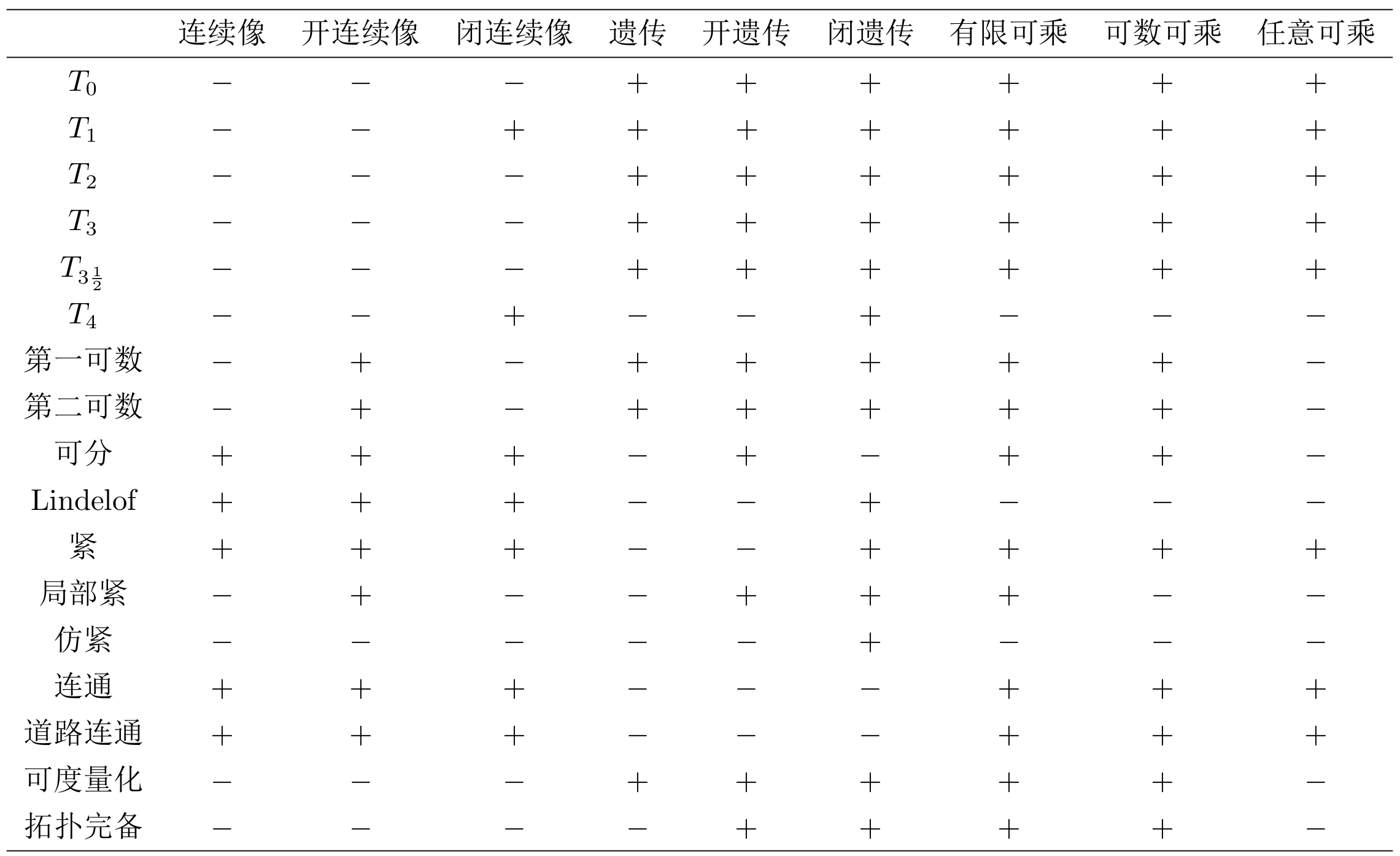
10. 拓朴不变量（拓扑性质）：两个同胚的拓扑空间之间相同的内秉性质

    • 任何只用开集和闭集描述的性质都是拓扑性质
    • 分离性
      • 点与点的分离
        • \(T_0\)：任意不同两点中有一点能用开集将其与另外一点分离 \(\iff\) 任意不同两点的闭包不相同
        • \(T_1\)：任意不同两点中每一点均能用开集将其与另外一点分离 \(\iff\) 任意单点集是闭集
          • \(T_1\implies \{x\}^\prime=\varnothing\) +（极限点 = ω 聚点）
        • \(T_2\)（Hausdorff）：任意不同的两点均能用两个不交开集分离 \(\iff\{(x,x)\mid x\in X\}\) 是乘积空间 \(X\times X\) 的闭子集 \(\iff\) 任意网至多有一个极限点
        • \(T_{2.5}\)（完全 Hausdorff）：对于 \(X\) 的任意相异两点 \(x,y\)，有 \(U\in\mathcal{U}(x), V\in\mathcal{U}(x)\),使得 \(\overline{U}\cap \overline{V}=\varnothing\)
      • 点与闭集的分离
        • \(T_3\)：\(T_0\) + 正则
          • 正则：任一闭集及不属于该闭集的点均能用两个不交开集分离 \(\iff\) 任给 \(X\) 中开集 \(U\) 以及 \(x\in U\)，存在开集 \(V\) 使得 \(x\in V\subseteq\overline{V}\subseteq U\)
        • \(T_{3.5}\)（吉洪诺夫，Tychonoff）：\(T_0\) + 完全正则
          • 完全正则：任给 \(X\) 的闭集 \(F\) 以及 \(x\not\in F\)，存在连续函数 \(f:X\rightarrow[0,1]\) 使得 \(f(x)=0, f(F)=\{1\}\)
      • 闭集与闭集的分离
        • \(T_4\)：\(T_1\) + 正规
          • 正规：任意两个不交闭集均能用两个不交开集分离 \(\iff\) 任给 \(X\) 中开集 \(U\) 以及闭集 \(F\)，若 \(F\subseteq U\)，则存在开集 \(V\) 使得 \(F\subseteq V\subseteq\overline{V}\subseteq U\)
          • Urysohn 引理：拓扑空间 \(X\) 正规 \(\iff\) 任给 \(X\) 的不交的非空闭集 \(A, B\)，存在连续函数 \(f: X\to [ 0, 1]\) 使得 \(f(A)=\{0\},f(B)=\{1\}.\)
      • 分离集合 \(A, B\)（\(\overline{A}\cap B=\varnothing=A\cap\overline{B}\)）的分离
        • \(T_5\)：\(T_1\) + 完全正规
          • 完全正规：任意两个分离集均能用两个不交开集分离 \(\iff\) 任意子空间正规
      • \(T_5\implies T_4\implies T_{3.5}\implies T_3\implies T_{2.5}\implies T_2\implies T_1\implies T_0\)
      • 完全正则 \(\implies\) 正则，完全正规 \(\implies\) 正规
      • 正则 + 正规 \(\implies\) 完全正则
      • Lindelof + 正则 \(\implies\) 正规
    • 可数性
      • 第一可数 \((C_1)\)：任意一点均有可数邻域基
      • 第二可数 \((C_2)\)：存在可数拓扑基
      • 可分 \((S)\)：存在可数稠密子集
      • \(C_2\implies C_1\)，\(S\)，Lindelof
    • 紧致性
      • 紧：任意开覆盖均有有限子覆盖 \(\iff\) 任意满足有限交性质的闭集族有非空的交 \(\iff\) 任意网有收敛子网（有聚点）\(\iff\) 任意超网均收敛 \(\iff\) 任意开覆盖有有限加细
        • 紧性（趋于偏弱）和 Hausdorff 性质（趋于偏强）彼此“对偶”：
          • 如果 \((X, \mathcal{T})\) 是紧空间，那么
            • \(X\) 中的闭子集都是紧集
            • \(\mathcal{T}^\prime\subset\mathcal{T}\implies (X, \mathcal{T}^\prime)\) 是紧空间
          • 如果 \((X, \mathcal{T})\) 是 Hausdorff 空间，那么
            • \(X\) 中的紧子集都是闭集
            • \(\mathcal{T}\subset\mathcal{T}^\prime\implies (X, \mathcal{T}^\prime)\) 是 Hausdorff 空间
        • 紧空间 \(X\) 到 Hausdorff 空间 \(Y\) 的连续映射是闭映射
        • 紧 + Hausdorff \(\implies T_4\)
        • 紧 Hausdorff 拓扑之间不可比较（互不包含）
          • 紧 Hausdorff 拓扑“恰到好处”：比其严格粗的拓扑紧但不 Hausdorff，比其严格细的拓扑 Hausdorff 但不紧
      • 序列紧：任意序列有收敛子序列（有序列聚点）
      • 子集紧（极限点紧，弱可数紧）：任意无穷子集必有极限点（导集非空）
      • 可数紧：任意可数开覆盖均有有限子覆盖 \(\iff\) 任意单减非空闭集列有非空的交（闭集套）\(\iff\) 任意无穷子集必有 ω 聚点 \(\iff\) 任意序列有收敛子网（有聚点）
      • Lindelof：任意开覆盖均有可数子覆盖
      • 局部紧
        • 局部紧 a：任意一点均有紧邻域
        • 局部紧 b（强局部紧）：任意一点均有闭的紧邻域 \(\iff\) 任意一点均含于某个具有紧闭包的开集
        • 局部紧 c：任意一点均有紧邻域基
        • 强局部紧 \(\xleftrightharpoons{+ T_2}\) 局部紧 a \(\xleftrightharpoons[+ T_2]{}\) 局部紧 c
      • 仿紧：任意开覆盖均有局部有限开加细
      • 紧 + 正则 \(\implies\) 局部紧 c
      • 可数紧 + Lindelof \(\iff\) 紧 \(\implies\) 强局部紧 + 仿紧
      • 序列紧 \(\xleftrightharpoons{+ SS}\) 可数紧 \(\xleftrightharpoons{+ T_1}\) 子集紧
      • \(C_2\implies\)（紧 = 可数紧 = 序列紧）
    • 连通性
      • 连通：不能写成两个非空不交开集的并 \(\iff\) 既开又闭集只有 \(\varnothing\) 与 \(X\iff X\) 到离散空间的连续映射是常值映射
        • 连通子集的闭包连通
        • 连续函数介值定理：设 \(X\) 是连通空间，\(f:X\to\mathbb{R}\) 连续，若存在 \(x,y\in X\) 使得 \(f(x)<a<f(y)\)，则存在 \(z\in X,\:f(z)=a.\)
        • 连通分支：极大连通子集（一定闭）
      • 局部连通：任意一点均有连通邻域基 \(\iff\) 存在连通拓扑基 \(\iff\) 任意开子集的连通分支必是开集
      • 道路连通：任意两点间总存在道路连接
        • 从 \(x\) 到 \(y\) 的道路 \(\alpha\colon[0,1]\to X\)：\(\alpha\) 连续并且 \(\alpha(0)=x, \alpha(1)=y\)
        • 道路连通分支；极大道路连通子集
      • 局部道路连通：任意一点均有道路连通的邻域基 \(\iff\) 存在道路连通拓扑基 \(\iff\) 任意开子集的道路连通分支必是开集
    • Baire 空间：任意非空开集都是第二纲集 \(\iff\) 可数个开的稠子集的交是稠子集
      • 完备度量空间是 Baire 空间
      • 紧 Hausdorff 空间是 Baire 空间
    • 可度量化：存在 \(X\) 上的度量 \(d\) 使得 \(\mathcal{T}=\mathcal{T}_d\)，即 \(d\) 诱导拓扑 \(\mathcal{T}\)
      • 可度量化 \(\implies T_5\) + \(C_1\) +（\(C_2\) = \(S\) = Lindelof）
      • 可度量化 \(\implies\)（紧 = 可数紧 = 序列紧 = 子集紧）
      • Urysohn 度量化定理：\(C_2\) + \(T_3\implies\) 可度量化
      • Nagata- Smirnov 度量化定理：可度量化 \(\iff T_{3}\) + 存在 \(\sigma\) 局部有限基
      • 度量空间 \(X\) 的性质
        • （完）全有界：对任意 \(\varepsilon>0\)，都存在有限多个半径为 \(\varepsilon\) 的球覆盖 \(X\iff\) 对任意 \(\varepsilon>0\)，\(X\) 中都存在有限 \(\varepsilon\) 网 \(N_\varepsilon\)
        • 完备：任意 Cauchy 序列均收敛
        • 紧 \(\iff\) 完全有界 + 完备
    • 拓扑完备：可完备度量化 \(\iff\) 同胚于某紧 Hausdorff 空间的一个可度量化的 \(G_\delta\) 集
    • 
    • 基本群

11. 代数结构、拓扑结构的等价

    • 同态（Homomorphism）：\(f(a)f(b)=f(ab)\)（保持代数结构）
    • 同构（Isomorphism）：一一对应的同态
    • 同胚（Homeo(morphism)）：\(f\) 连续、双射且逆映射连续（保持拓扑结构）