矩阵分解与矩阵求导

基础

1. 向量运算：（模长 \(\vert \boldsymbol{x}\vert=\Vert \boldsymbol{x}\Vert_2\)）
   • 内积（inner product，数量积，点乘）：\(\boldsymbol{x}\cdot \boldsymbol{y}=\sum_{i=1}^n x_i^*y_i=\boldsymbol{x}^\mathrm{H}\boldsymbol{y}=\vert \boldsymbol{x}\vert \vert \textcolor{blue}{\boldsymbol{y}\vert \cos\theta（\boldsymbol{y}\text{ 到 }\boldsymbol{x}\text{ 的投影）}}\)
   • 外积（exterior product，向量积，叉乘）：\(\vert \boldsymbol{x}\times \boldsymbol{y}\vert=\vert \boldsymbol{x}\vert \vert \boldsymbol{y}\vert \sin\theta\)（右手定则）
   • 外积（outer product）：\(\boldsymbol{x}\circ \boldsymbol{y}=\boldsymbol{x}\boldsymbol{y}^\mathrm{H}=\boldsymbol{x}\otimes \boldsymbol{y}^\mathrm{H}\)
2. 矩阵运算：（\(\boldsymbol{A}=\left(\boldsymbol{c}_1,\cdots,\boldsymbol{c}_m\right)=\left(\boldsymbol{r}_1,\cdots,\boldsymbol{r}_n\right)^\top \in \mathbb{C}^{n \times m}\)）
   • 乘积：\(\left(\boldsymbol{\boldsymbol{A}}\boldsymbol{B}\right)_{ij}=\sum_{k=1}^m a_{ik}b_{kj}\)
     • 左乘变行 \(\boldsymbol{x}^\top \boldsymbol{A}=\boldsymbol{x}^\top \left(\boldsymbol{r}_1,\cdots,\boldsymbol{r}_n\right)^\top =\sum_{k=1}^n x_i \boldsymbol{r}_i^\top =\boldsymbol{x}^\top \left(\boldsymbol{c}_1,\cdots,\boldsymbol{c}_m\right)=\left(\boldsymbol{x}^\top \boldsymbol{c}_1,\cdots,\boldsymbol{x}^\top \boldsymbol{c}_m\right)\)
     • 右乘变列 \(\boldsymbol{A}\boldsymbol{x}=\left(\boldsymbol{c}_1,\cdots,\boldsymbol{c}_m\right)\boldsymbol{x}=\sum_{k=1}^m x_i \boldsymbol{c}_i=\left(\boldsymbol{r}_1,\cdots,\boldsymbol{r}_n\right)^\top \boldsymbol{x}=\left(\boldsymbol{r}_1^\top \boldsymbol{x},\cdots,\boldsymbol{r}_n^\top \boldsymbol{x}\right)^\top\)
   • Hadamard 积（逐分量积，Schur 积）：\(\left(\boldsymbol{A} \odot \boldsymbol{B}\right)_{ij}=a_{ij}b_{ij}\)
     • \(\left(\boldsymbol{x}\boldsymbol{x}^\mathrm{H}\right)\circ\left(\boldsymbol{y}\boldsymbol{y}^\mathrm{H}\right)=\left(\boldsymbol{x}\circ \boldsymbol{y}\right)\left(\boldsymbol{x}\circ \boldsymbol{y}\right)^\mathrm{H}\)
     • \(\boldsymbol{x}^*\left(\boldsymbol{y}\circ \boldsymbol{z}\right)=\left(\boldsymbol{x}\circ \boldsymbol{y}^*\right)^\mathrm{H}\boldsymbol{z}\)
   • 内积（inner product，数量积，点乘）：\(\langle \boldsymbol{A},\boldsymbol{B}\rangle=\boldsymbol{A}\cdot \boldsymbol{B}=\sum_{i=1}^n \sum_{j=1}^m a_{ij}^*b_{ij}=\operatorname{tr}\left(\boldsymbol{A}^\mathrm{H}\boldsymbol{B}\right)\)
     • \(\langle \boldsymbol{A},\boldsymbol{B}\rangle\leqslant \Vert \boldsymbol{A}\Vert_p\Vert \boldsymbol{B}\Vert_q, \ p,q\) 共轭
   • Kronecker 积（直积，圈乘）：\(\boldsymbol{A}\otimes \boldsymbol{B}=\begin{pmatrix}a_{11}\boldsymbol{B}&\cdots&a_{1m}\boldsymbol{B}\\ \vdots&\ddots&\vdots\\a_{n1}\boldsymbol{B}&\cdots&a_{nm}\boldsymbol{B}\end{pmatrix}\)
     • \(\left(\boldsymbol{A}\otimes \boldsymbol{B}\right)^\mathrm{H}=\boldsymbol{A}^\mathrm{H}\otimes \boldsymbol{B}^\mathrm{H}, \left(\boldsymbol{A}\otimes \boldsymbol{B}\right)^-=\boldsymbol{A}^-\otimes \boldsymbol{B}^-\)
     • \(\operatorname{rank}\left(\boldsymbol{A}\otimes \boldsymbol{B}\right)=\operatorname{rank}\left(\boldsymbol{A}\right)\operatorname{rank}\left(\boldsymbol{B}\right), \operatorname{tr}\left(\boldsymbol{A}\otimes \boldsymbol{B}\right)=\operatorname{tr}\left(\boldsymbol{A}\right)\operatorname{tr}\left(\boldsymbol{B}\right)\)
     • \(\left(\boldsymbol{A}\boldsymbol{B}\right)\otimes\left(\boldsymbol{C}\boldsymbol{D}\right)=\left(\boldsymbol{A}\otimes \boldsymbol{C}\right)\left(\boldsymbol{B}\otimes \boldsymbol{D}\right)\)
     • \(\boldsymbol{\lambda}(\boldsymbol{A}\otimes \boldsymbol{B})=\{\lambda_i(\boldsymbol{A})\lambda_j(\boldsymbol{B})\}\)，特征向量集合 \(\mathcal{U}(\boldsymbol{A}\otimes \boldsymbol{B})=\{\boldsymbol{u}_i\otimes \boldsymbol{v}_j|\boldsymbol{u}_i\in\mathcal{U}(\boldsymbol{A}),\boldsymbol{v}_j\in\mathcal{U}(\boldsymbol{B})\}\)
   • 向量化（vectorization，列堆栈）：\(\operatorname{vec}\left(\boldsymbol{A}\right)=[\boldsymbol{c}_{1}^\top ,\cdots,\boldsymbol{c}_{m}^\top ]^\top\)
     • \(\operatorname{tr}\left(\boldsymbol{A}^\mathrm{H}\boldsymbol{B}\right)=\operatorname{vec}\left(\boldsymbol{A}\right)^\mathrm{H}\operatorname{vec}\boldsymbol{B}\)
     • \(\operatorname{vec}\left(\boldsymbol{A}^\top \right)=\boldsymbol{K}_{nm}\operatorname{vec}\left(\boldsymbol{A}\right)\)
     • \(\boldsymbol{K}_{nm}=\sum_{j=1}^m\left(\boldsymbol{e}_i^\top \otimes \boldsymbol{I}_n\otimes \boldsymbol{e}_i\right)=\boldsymbol{K}_{mn}^{-1}=\boldsymbol{K}_{mn}^{\top }\)
     • \(\boldsymbol{K}_{pn}\left(\boldsymbol{A}_{n\times m}\otimes \boldsymbol{B}_{p\times q}\right)\boldsymbol{K}_{mq}=\boldsymbol{B}\otimes \boldsymbol{A}\)
     • \(\operatorname{vec}\left(\boldsymbol{A}\boldsymbol{B}\boldsymbol{C}\right)=\left(\boldsymbol{C}^\top \otimes \boldsymbol{A}\right)\operatorname{vec}\left(\boldsymbol{B}\right)\)
3. 范数：非负性，绝对（模）齐次性，次可加性（三角不等式）；
   • 复数模的推广，\(a\leqslant|z|=\sqrt{a^2+b^2}=\sqrt{z^*z}, z=a+b\mathrm{i}\)
   • 有限维赋范线性空间范数等价（诱导相同的拓扑）
   • 向量范数 \(\boldsymbol{x}\in \mathbb{C}^n\)：（\(\Vert \boldsymbol{x}\Vert_p=\sqrt[p]{\sum_{i=1}^n \vert x_i \vert^p}\)）
     • \(1\leqslant p\leqslant+\infty\) 时为范数
     • \(\Vert \boldsymbol{x}\Vert_1=\sum_{i=1}^n \vert x_i \vert\)（曼哈顿距离）
     • \(\Vert \boldsymbol{x}\Vert_2=\sqrt{\boldsymbol{x}^\mathrm{H}\boldsymbol{x}}=\sqrt{\sum_{i=1}^n \vert x_i \vert^2}\)（欧氏距离）
     • \(\Vert \boldsymbol{x}\Vert_\infty=\displaystyle\max_{1\leqslant i\leqslant n} \vert x_i \vert\)（切比雪夫距离 ）
     • 
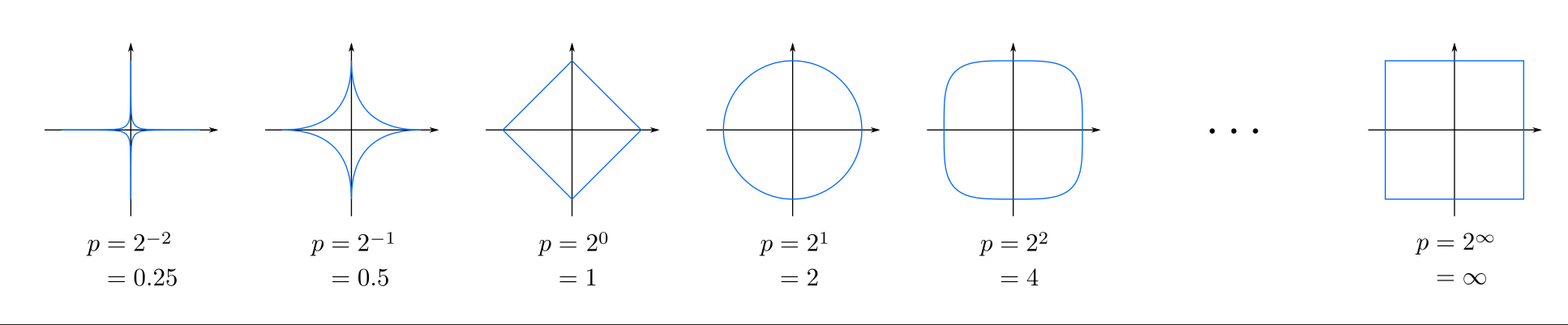
     • \(1\leqslant p<q\leqslant +\infty:n^{1/q-1/p}\|\boldsymbol{x}\|_p\leqslant \|\boldsymbol{x}\|_q\leqslant \|\boldsymbol{x}\|_p\)
   • 矩阵范数 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}\)：（相容性/次可乘性：\(\Vert \boldsymbol{A}\boldsymbol{B}\Vert \leqslant \Vert \boldsymbol{A}\Vert \Vert \boldsymbol{B}\Vert\)）
     • 逐元素（entrywise）范数 \(\Vert \boldsymbol{A}\Vert_{l_p}=\sqrt[p]{\sum_{i=1}^n \sum_{j=1}^m \vert a_{ij} \vert^p}\)（列堆栈后向量范数）
       • \(\ell_1\) 范数 \(\Vert \boldsymbol{A}\Vert_{\ell_1}=\sum_{i=1}^n\sum_{j=1}^m \vert a_{ij} \vert\)
       • F 范数 \(\Vert \boldsymbol{A}\Vert_{\ell_2}=\Vert \boldsymbol{A}\Vert_{F}=\sqrt{\operatorname{tr}\left(\boldsymbol{A}^\mathrm{H}\boldsymbol{A}\right)}=\sqrt{\sum_{i=1}^n \sum_{j=1}^m \vert a_{ij} \vert^2}\)
       • \(\ell_\infty\) 范数 \(\Vert \boldsymbol{A}\Vert_{\ell_\infty}=\displaystyle\max_{1\leqslant i\leqslant n, 1\leqslant j\leqslant m} \vert a_{ij} \vert\)（其 \(m\) 倍相容）
     • 算子（operator）范数 \(\Vert \boldsymbol{A}\Vert_{a,b}=\displaystyle\max_{\Vert \boldsymbol{x} \Vert_a\leqslant 1}\Vert \boldsymbol{A}\boldsymbol{x}\Vert_b\)（由向量范数诱导的从属范数，作为线性变换作用到单位向量上的最大伸缩倍数）
       • 最大绝对列和范数 \(\Vert \boldsymbol{A}\Vert _1=\displaystyle\max_{1\leqslant j\leqslant m}\sum_{i=1}^n|a_{ij}|\)
       • 谱范数（2 范数） \(\Vert \boldsymbol{A}\Vert _2=\sqrt{\lambda_{\max}\left(\boldsymbol{A}^\mathrm{H}\boldsymbol{A}\right)}=\sigma_{\max}\left(\boldsymbol{A}\right)\)
       • 最大绝对行和范数 \(\Vert \boldsymbol{A}\Vert _\infty=\displaystyle\max_{1\leqslant i\leqslant n}\sum_{j=1}^m|a_{ij}|\)
     • Schatten 范数 \(\Vert \boldsymbol{A}\Vert_{s_p}=\sqrt[p]{\sum_{i=1}^r \sigma_i^p\left(\boldsymbol{A}\right)}\)（由矩阵奇异值定义的范数，酉不变）
       • 核范数 \(\Vert \boldsymbol{A}\Vert_{s_1}=\Vert \boldsymbol{A}\Vert _*=\operatorname{tr}\left(\sqrt{\boldsymbol{A}^\mathrm{H}\boldsymbol{A}}\right)=\sum_{i=1}^r \sigma_i\left(\boldsymbol{A}\right)\)（矩阵秩的凸包络，即最佳凸逼近 / 凸松弛）
       • \(s_2\) 范数 \(\Vert \boldsymbol{A}\Vert_{s_2}=\Vert \boldsymbol{A}\Vert_{F}=\sqrt{\sum_{i=1}^r \sigma_i\left(\boldsymbol{A}\right)^2}\)（自对偶）
       • \(s_\infty\) 范数 \(\Vert \boldsymbol{A}\Vert_{s_\infty}=\Vert \boldsymbol{A}\Vert_{2}\)（与核范数互为对偶范数）
   • 矩阵范数不等式：
     • \(1\leqslant p<q\leqslant\infty:m^{\frac1q-\frac1p}\Vert \boldsymbol{A}\Vert _q\leqslant\Vert \boldsymbol{A}\Vert _p\leqslant n^{\frac1p-\frac1q}\Vert \boldsymbol{A}\Vert _q\)
     • \(\Vert \boldsymbol{A}\Vert_2\leqslant\Vert \boldsymbol{A}\Vert _F\leqslant \sqrt{\min\{m,n\}}\Vert \boldsymbol{A}\Vert _2\)
4. 矩阵 \(\boldsymbol{A}, \boldsymbol{B}\in\mathbb{C}^{n\times n}\) 的等价关系
   • 相抵（\(\boldsymbol{A}\cong \boldsymbol{B}\)）：\(\boldsymbol{B}=\boldsymbol{\boldsymbol{P}}\boldsymbol{A}\boldsymbol{Q}\)，其中 \(\boldsymbol{\boldsymbol{P}}, \boldsymbol{Q}\) 可逆 \(\iff\) 秩相同
     • 初等行变换：行阶梯型、简化行阶梯型（唯一）
     • 初等行列变换：相抵标准型（唯一）
   • 相似（\(\boldsymbol{A}\sim \boldsymbol{B}\)）：\(\boldsymbol{B}=\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}\) \(\iff\) Jordan 标准型（不计 Jordan 块顺序时唯一）相同
     • 同一个线性变换在不同基下的表示矩阵
     • 线性变换 \(\sigma\) 在基 \((\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n)\) 下的表示矩阵为 \(\boldsymbol{A}\)：\(\sigma(\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n)=(\boldsymbol{x}_1,\cdots,\boldsymbol{x}_n)\boldsymbol{A}\)
     • \(\boldsymbol{P}\)：过渡矩阵
   • 合同（\(\boldsymbol{A}\simeq \boldsymbol{B}\)）：\(\boldsymbol{B}=\boldsymbol{P}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{P}\) \(\iff\) 正负惯性指数相同
     • 同一个二次型（双线性型）在不同基下的对应矩阵
5. 矩阵 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}\) 的性能指标
   • 二次型 \(\boldsymbol{x}^H\boldsymbol{A}\boldsymbol{x}\to\) （半）正定性
     • 每个二次型对应唯一的 Hermite 矩阵以及该矩阵的合同等价类
     • \(\boldsymbol{A}\in\mathcal{H}^n\) 正定 \(\iff \lambda(\boldsymbol{A})>0\iff\) 每个主子阵正定 \(\iff\) 每个主子式 \(>0\)
     • Lowner-Heinz 定理：\(\boldsymbol{A}\preceq \boldsymbol{B}\preceq\boldsymbol{0},0\leqslant r\leqslant 1\implies \boldsymbol{A}^r\preceq \boldsymbol{B}^r\)
   • 行列式 \(\det(\boldsymbol{A})=|\boldsymbol{A}|=\displaystyle\prod_{1\leqslant i\leqslant n}\lambda_{i}\left(\boldsymbol{A}\right)\to\) 奇异性
     • 行列式是矩阵行（列）向量组构成的平行多面体的有向体积，是矩阵作为线性变换对有向体积的伸缩倍数
     • 余子式 \(M_{ij}\)，代数余子式 \(A_{ij}=\left( -1 \right)^{i+j}M_{ij}\)
     • 矩阵行列式等于其任意行（列）的元素与相对应的代数余子式乘积之和
     • \(|\boldsymbol{A}\boldsymbol{B}|=|\boldsymbol{A}|\cdot|\boldsymbol{B}|\)
   • 迹 \(\mathrm{tr}(\boldsymbol{A})=\displaystyle\sum_{1\leqslant i\leqslant n}a_{ii}=\displaystyle\sum_{1\leqslant i\leqslant n}\lambda_{i}\left( \boldsymbol{A} \right)\)
     • \(\mathrm{tr}(\boldsymbol{A}\boldsymbol{B})=\mathrm{tr}(\boldsymbol{B}\boldsymbol{A})\)
   • 秩 \(\operatorname{rank}(\boldsymbol{A})=\operatorname{dim}\mathcal{R}(\boldsymbol{A})\)
     • \(\operatorname{dim}\mathcal{R}(\boldsymbol{A})+\operatorname{dim}\mathcal{N}(\boldsymbol{A})\)（零度）\(=n\)
     • \(\operatorname{rank}(\boldsymbol{A}\boldsymbol{B})\leqslant\min \{\operatorname{rank}(\boldsymbol{A}),\operatorname{rank}(\boldsymbol{B})\}\)
6. 对于方阵 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}\)，谱半径 \(\rho\left(\boldsymbol{A}\right):=\displaystyle\max_{1\leqslant i\leqslant n}\vert \lambda_{i}\left(\boldsymbol{A}\right)\vert\)；
   • 对于任意相容范数 \(\Vert \cdot\Vert\)，均成立 \(\rho\left(\boldsymbol{A}\right)\leqslant\Vert \boldsymbol{A}\Vert\)
   • \(\forall\varepsilon>0, \exists \Vert \cdot\Vert\ \text{s.t.}\ \Vert \boldsymbol{A}\Vert <\rho\left(\boldsymbol{A}\right)+\varepsilon\)，即 \(\rho\left(\boldsymbol{A}\right)=\displaystyle\inf_{\Vert \cdot\Vert \text{为相容范数}}\Vert \boldsymbol{A}\Vert\)
   • \(\boldsymbol{A}\) 正规 \(\implies \rho(\boldsymbol{A})=\|\boldsymbol{A}\|_2\)
   • \(\rho\left(\boldsymbol{A}\right)=\displaystyle\lim_{k\to+\infty}\Vert \boldsymbol{A}^k\Vert ^{\frac1k}\)
   • \(\rho\left(\boldsymbol{A}\right)<1\iff\sum_{k=0}^\infty \boldsymbol{A}^k\) 收敛；收敛时极限为 \(\left(\boldsymbol{I}-\boldsymbol{A}\right)^{-1}\)
7. 对于方阵 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}\)，条件数 \(\kappa \left(\boldsymbol{A}\right):=\lVert \boldsymbol{A} \rVert \lVert \boldsymbol{A}^{-1} \rVert\)，表征矩阵 \(\boldsymbol{A}\) 对向量的伸缩能力；
   • 条件数刻画了求解线性方程组 \(\boldsymbol{A} \boldsymbol{x}=\boldsymbol{b}\) 时，误差经过矩阵 \(\boldsymbol{A}\) 的传播扩大为解向量的误差的程度，是衡量线性方程组数值稳定性的重要指标
   • 取 \(\lVert \cdot \rVert =\lVert \cdot \rVert_2\)，\(\kappa \left( \boldsymbol{A} \right)=\sigma_{max}\left( \boldsymbol{A} \right)/\sigma_{min}\left( \boldsymbol{A} \right)\)
   • \(\boldsymbol{A}\left( \boldsymbol{x}+\Delta \boldsymbol{x} \right)=\boldsymbol{b}+\Delta \boldsymbol{b}\implies\frac{1}{\kappa\left( \boldsymbol{A} \right)}\frac{\lVert \Delta \boldsymbol{b} \rVert }{\lVert \boldsymbol{b} \rVert }\leqslant \frac{\lVert \Delta \boldsymbol{x} \rVert }{\lVert \boldsymbol{x} \rVert }\leqslant \kappa\left( \boldsymbol{A} \right)\frac{\lVert \Delta \boldsymbol{b} \rVert }{\lVert \boldsymbol{b} \rVert }\)
   • \(\left( \boldsymbol{A} +\Delta \boldsymbol{A}\right)\left( \boldsymbol{x}+\Delta \boldsymbol{x} \right)=\boldsymbol{b}\implies \frac{\lVert \Delta \boldsymbol{x} \rVert }{\lVert \boldsymbol{x} +\Delta\boldsymbol{x}\rVert }\leqslant \kappa\left( \boldsymbol{A} \right)\frac{\lVert \Delta \boldsymbol{A}\rVert }{\lVert \boldsymbol{A} \rVert }\)
8. 矩阵方程 \(\boldsymbol{A}\boldsymbol{X}\boldsymbol{B}=\boldsymbol{D}, \boldsymbol{A}\in\mathbb{C}^{m\times n}, \boldsymbol{B}\in\mathbb{C}^{p\times q}, \boldsymbol{D}\in\mathbb{C}^{m\times q}\)
   • 有解（相容）\(\iff \boldsymbol{A}\boldsymbol{A}^-\boldsymbol{D}\boldsymbol{B}^-\boldsymbol{B}=\boldsymbol{D}\)，通解 \(\boldsymbol{X}=\boldsymbol{A}^-\boldsymbol{D}\boldsymbol{B}^-+\boldsymbol{Y}-\boldsymbol{A}^-\boldsymbol{A}\boldsymbol{Y}\boldsymbol{B}\boldsymbol{B}^-\in\mathbb{C}^{n\times p}\)，其中 \(\boldsymbol{Y}\in\mathbb{C}^{n\times p}\) 任意
     • \(\boldsymbol{A}\boldsymbol{X}=\boldsymbol{D}\) 相容 \(\iff \boldsymbol{A}\boldsymbol{A}^-\boldsymbol{D}=\boldsymbol{D}\)，通解 \(\boldsymbol{X}=\boldsymbol{A}^-\boldsymbol{D}+\left( \boldsymbol{I}_n-\boldsymbol{A}^-\boldsymbol{A} \right)\boldsymbol{Y}\in\mathbb{C}^{n\times p}\)，其中 \(\boldsymbol{Y}\in\mathbb{C}^{n\times p}\) 任意
     • \(\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}\) 相容 \(\iff\boldsymbol{b}\in\mathcal{R}(\boldsymbol{A})\iff \boldsymbol{A}\boldsymbol{A}^-\boldsymbol{b}=\boldsymbol{b}\)，通解 \(\boldsymbol{x}=\boldsymbol{A}\{1\}\boldsymbol{b}=\boldsymbol{A}^-\boldsymbol{b}+\left( \boldsymbol{I}_n-\boldsymbol{A}^-\boldsymbol{A} \right)\boldsymbol{y}\in\mathbb{C}^{n}\)，其中 \(\boldsymbol{y}\in\mathbb{C}^{n}\) 任意
       • 不相容方程 \(\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}\) 的最小二乘解：\(\boldsymbol{A}\{1,3\}\boldsymbol{b}=\{\boldsymbol{x}\in\mathbb{C}^{n} |\boldsymbol{A}^\mathrm{H}\boldsymbol{A}\boldsymbol{x}=\boldsymbol{A}^\mathrm{H}\boldsymbol{b}\}\)
         • 唯一极小范数最小二乘解：\(\boldsymbol{A}^\dag\boldsymbol{b}\)
       • 相容方程 \(\boldsymbol{A}\boldsymbol{x}=\boldsymbol{b}\) 的唯一极小范数解：\(\boldsymbol{A}\{1,4\}\boldsymbol{b}\in\mathcal{R}(\boldsymbol{A}^\mathrm{H})\)
9. \(\boldsymbol{A}=\boldsymbol{U}\begin{pmatrix}\boldsymbol{\Sigma}_r&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{0}\end{pmatrix}\boldsymbol{V}^{\mathrm{H}}\in\mathbb{C}^{m\times n}_r\) 的广义逆
   • Penrose 方程（\(\boldsymbol{X}=\boldsymbol{V}\begin{pmatrix}\boldsymbol{A}&\boldsymbol{B}\\\boldsymbol{C}&\boldsymbol{D}\end{pmatrix}\boldsymbol{U}^{\mathrm{H}}\)）
     • \((1)\ \boldsymbol{A}\boldsymbol{X}\boldsymbol{A}=\boldsymbol{A}\iff \boldsymbol{A}=\boldsymbol{\Sigma}_r^{-1}\)
     • \((2)\ \boldsymbol{X}\boldsymbol{A}\boldsymbol{X}=\boldsymbol{X}\iff \boldsymbol{C}\boldsymbol{\Sigma}_r\boldsymbol{B}=\boldsymbol{D}\)
     • \((3)\ \left( \boldsymbol{A}\boldsymbol{X} \right)^{\mathrm{H}}=\boldsymbol{A}\boldsymbol{X}\iff \boldsymbol{B}=\boldsymbol{0}\)
     • \((4)\ \left( \boldsymbol{X}\boldsymbol{A} \right)^{\mathrm{H}}=\boldsymbol{X}\boldsymbol{A}\iff \boldsymbol{C}=\boldsymbol{0}\)
   • Moore 广义逆：\(\boldsymbol{A}\boldsymbol{X}=\boldsymbol{P}_{\mathcal{R}(\boldsymbol{A})}, \boldsymbol{X}\boldsymbol{A}=\boldsymbol{P}_{\mathcal{R}(\boldsymbol{A}^{\mathrm{H}})}\)
     • 投影矩阵：对于直和分解 \(\mathbb{C}^n=L\oplus M\)，沿 \(M\) 到 \(L\) 的投影变换在标准正交基下对应的矩阵 \(\boldsymbol{P}_{L,M}\)
       • 正交投影矩阵：\(\boldsymbol{P}_{L,M}^{\mathrm{H}}=\boldsymbol{P}_{L,M}\iff M=L^{\perp}\)（与幂等 Hermite 矩阵一一对应）
         • \((\mathcal{R}(\boldsymbol{A}))^\perp=\mathcal{N}(\boldsymbol{A}^\mathrm{H})\)
         • \((\mathcal{R}(\boldsymbol{A}^{\mathrm{H}}))^\perp=\mathcal{N}(\boldsymbol{A})\)
       • \(\boldsymbol{P}_1=\boldsymbol{P}_{\boldsymbol{R}_1,N_1}, \boldsymbol{P}_2=\boldsymbol{P}_{\boldsymbol{R}_2,N_2}\)
         • \(\boldsymbol{P}_1\boldsymbol{P}_2=\boldsymbol{P}_2\boldsymbol{P}_1=\boldsymbol{0}\iff \boldsymbol{P}_1+\boldsymbol{P}_2=\boldsymbol{P}_{\boldsymbol{R}_1\oplus \boldsymbol{R}_2,N_1\cap N_2}\)
         • \(\boldsymbol{P}_1\boldsymbol{P}_2=\boldsymbol{P}_2\boldsymbol{P}_1=\boldsymbol{P}_2\iff \boldsymbol{P}_1+\boldsymbol{P}_2=\boldsymbol{P}_{\boldsymbol{R}_1\cap N_2,N_1\oplus \boldsymbol{R}_2}\)
     • 幂等矩阵：\(\boldsymbol{P}^2=\boldsymbol{P}\)（与投影矩阵一一对应 \(\boldsymbol{P}=\boldsymbol{P}_{\mathcal{R}(\boldsymbol{P}),\mathcal{N}(\boldsymbol{P})}\)）
       • \(\boldsymbol{P}^{\mathrm{H}}, \boldsymbol{I}-\boldsymbol{P}\) 幂等
       • \(\lambda(\boldsymbol{P})\in\{0,1\}, \sharp(\lambda_i(\boldsymbol{P})=1)=\operatorname{rank}\boldsymbol{P}=\operatorname{tr}\boldsymbol{P}\)
       • \(\boldsymbol{P}\boldsymbol{x}=\boldsymbol{x}\iff\boldsymbol{x}\in\mathcal{R}(\boldsymbol{P})\)
       • 满秩分解 \(\boldsymbol{P}=\boldsymbol{F}\boldsymbol{G}\implies \boldsymbol{G}\boldsymbol{F}=\boldsymbol{I}\)
   • 减号逆 \(\boldsymbol{A}^-:=\boldsymbol{A}^{(1)}\)
     • \(\boldsymbol{X}\in \boldsymbol{A}\{1\}\iff \boldsymbol{X}\boldsymbol{A}\text{ 幂等且 }\operatorname{rank}(\boldsymbol{X}\boldsymbol{A})=\operatorname{rank}\boldsymbol{A}\iff \boldsymbol{A}\boldsymbol{X}\text{ 幂等且 }\operatorname{rank}(\boldsymbol{A}\boldsymbol{X})=\operatorname{rank}\boldsymbol{A}\)
     • \(\boldsymbol{A}\{1\}=\{\boldsymbol{A}^-+\boldsymbol{Z}-\boldsymbol{A}^-\boldsymbol{A}\boldsymbol{Z}\boldsymbol{A}\boldsymbol{A}^-|\boldsymbol{Z}\in\mathbb{C}^{n\times m}\}\)
     • \((\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A})^-\boldsymbol{A}^{\mathrm{H}}\in \boldsymbol{A}\{1,2,3\},\boldsymbol{A}^{\mathrm{H}}(\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}})^-\in \boldsymbol{A}\{1,2,4\}\)
     • \(\operatorname{rank}\boldsymbol{A}\leqslant\operatorname{rank}\boldsymbol{A}^-\)
     • \(\operatorname{rank}\boldsymbol{A}=n\iff \mathcal{N}(\boldsymbol{A})=\{\boldsymbol{0}\}\iff\)左逆存在
       • \(\boldsymbol{A}^{-1}_L=\boldsymbol{A}\{1\}=\boldsymbol{A}\{1,2,4\}=\{(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{G}\boldsymbol{A})^{-1}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{G}|\operatorname{rank}(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{G}\boldsymbol{A})=\operatorname{rank}\boldsymbol{A}\}\)
       • \(\boldsymbol{A}^\dag=(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A})^{-1}\boldsymbol{A}^{\mathrm{H}}\)
     • \(\operatorname{rank}\boldsymbol{A}=m\iff \mathcal{R}(\boldsymbol{A})=\mathbb{C}^m\iff\)右逆存在
       • \(\boldsymbol{A}^{-1}_R=\boldsymbol{A}\{1\}=\boldsymbol{A}\{1,2,3\}=\{\boldsymbol{G}\boldsymbol{A}^{\mathrm{H}}(\boldsymbol{A}\boldsymbol{G}\boldsymbol{A}^{\mathrm{H}})^{-1}|\operatorname{rank}(\boldsymbol{A}\boldsymbol{G}\boldsymbol{A}^{\mathrm{H}})=\operatorname{rank}\boldsymbol{A}\}\)
       • \(\boldsymbol{A}^\dag=\boldsymbol{A}^{\mathrm{H}}(\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}})^{-1}\)
     • \(\boldsymbol{A}^\mathrm{H}(\boldsymbol{A}\boldsymbol{A}^\mathrm{H})^-\boldsymbol{A}\) 不依赖减号逆选取
       • \(\boldsymbol{A}\boldsymbol{B}(\boldsymbol{A}\boldsymbol{B})^-\boldsymbol{A}=\boldsymbol{A}\iff \operatorname{rank}(\boldsymbol{A}\boldsymbol{B})=\operatorname{rank}\boldsymbol{A}\)
       • \(\boldsymbol{B}(\boldsymbol{A}\boldsymbol{B})^-\boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}\iff\operatorname{rank}(\boldsymbol{A}\boldsymbol{B})=\operatorname{rank}\boldsymbol{B}\)
   • 自反减号逆 \(\boldsymbol{A}^-_r:=\boldsymbol{A}^{(1,2)}\)
     • \(\boldsymbol{X}\in \boldsymbol{A}\{1,2\}\iff \boldsymbol{X}\in \boldsymbol{A}\{1\}, \operatorname{rank}\boldsymbol{X}=\operatorname{rank}\boldsymbol{A}\)
     • \(\boldsymbol{X}, \boldsymbol{Y}\in \boldsymbol{A}\{1\}\implies \boldsymbol{X}\boldsymbol{A}\boldsymbol{Y}\in \boldsymbol{A}\{1,2\}\)
   • 最小二乘广义逆 \(\boldsymbol{A}^-_l:=\boldsymbol{A}^{(1,3)}\)
     • \(\boldsymbol{X}\in \boldsymbol{A}\{1,3\}\iff \boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{X}=\boldsymbol{A}^{\mathrm{H}}\iff \boldsymbol{A}\boldsymbol{X}=\boldsymbol{P}_{\mathcal{R}(\boldsymbol{A})}\iff \boldsymbol{A}\boldsymbol{X}=\boldsymbol{A}^{(1,3)}\boldsymbol{A}\)
     • \(\boldsymbol{A}\{1,3\}=\{\boldsymbol{A}^-_l+(\boldsymbol{I}_n-\boldsymbol{A}^-_l\boldsymbol{A})\boldsymbol{V}|\boldsymbol{V}\in\mathbb{C}^{n\times m}\}\)
   • 极小范数广义逆 \(\boldsymbol{A}^-_m:=\boldsymbol{A}^{(1,4)}\)
     • \(\boldsymbol{X}\in \boldsymbol{A}\{1,4\}\iff \boldsymbol{X}\boldsymbol{A}\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}\iff \boldsymbol{X}\boldsymbol{A}=\boldsymbol{P}_{\mathcal{R}(\boldsymbol{A}^{\mathrm{H}})}\iff \boldsymbol{X}\boldsymbol{A}=\boldsymbol{A}^{(1,4)}\boldsymbol{A}\)
     • \(\boldsymbol{A}\{1,4\}=\{\boldsymbol{A}^-_m+\boldsymbol{Y}(\boldsymbol{I}_m-\boldsymbol{A}\boldsymbol{A}^-_m)|\boldsymbol{Y}\in\mathbb{C}^{n\times m}\}\)
   • 加号逆 \(\boldsymbol{A}^\dag:=\boldsymbol{A}^{(1,2,3,4)}\) 存在且唯一
     • \(\boldsymbol{A}^\dag=\boldsymbol{A}^{(1,4)}\boldsymbol{A}\boldsymbol{A}^{(1,3)}=(\boldsymbol{A}^\mathrm{H}\boldsymbol{A})^\dagger \boldsymbol{A}^\mathrm{H}=\boldsymbol{A}^\mathrm{H}(\boldsymbol{A}\boldsymbol{A}^\mathrm{H})^\dagger\)
     • \(( \boldsymbol{A}^{\dag} )^\dag=\boldsymbol{A}, (\boldsymbol{A}^{\mathrm{H}})^\dag=(\boldsymbol{A}^\dag)^{\mathrm{H}}\)
     • \(\mathcal{R}(\boldsymbol{A}^\dag)=\mathcal{R}(\boldsymbol{A}^\mathrm{H}), \mathcal{N}(\boldsymbol{A}^\dag)=\mathcal{N}(\boldsymbol{A}^\mathrm{H})\)
     • 反序法则：\((\boldsymbol{A}\boldsymbol{B})^{\dagger}=\boldsymbol{B}^{\dagger}\boldsymbol{A}^{\dagger}\) 的充要条件
       • \(\mathcal{R}(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B})\subseteq\mathcal{R}(\boldsymbol{B}), \mathcal{R}(\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}})\subseteq\mathcal{R}(\boldsymbol{A}^{\mathrm{H}})\)
         • \(\mathcal{R}(\boldsymbol{B})\) 和 \(\mathcal{R}(\boldsymbol{A}^{\mathrm{H}})\) 分别为 \(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\) 和 \(\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\) 的不变子空间
       • \(\boldsymbol{A}^{\dagger}\boldsymbol{A}\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}, \boldsymbol{B}\boldsymbol{B}^{\dagger}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B}=\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B}\)
       • \(\boldsymbol{A}^{\dagger}\boldsymbol{A}\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\) 和 \(\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B}\boldsymbol{B}^{\dagger}\) 均为 Hermite 矩阵
       • \(\boldsymbol{A}^{\dagger}\boldsymbol{A}\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B}\boldsymbol{B}^{\dagger}=\boldsymbol{B}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\)
       • \(\boldsymbol{A}^{\dagger}\boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}(\boldsymbol{A}\boldsymbol{B})^{\dagger}\boldsymbol{A}\boldsymbol{B}, \boldsymbol{B}\boldsymbol{B}^{\dagger}\boldsymbol{A}^{\mathrm{H}}=\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\boldsymbol{B}(\boldsymbol{A}\boldsymbol{B})^{\dagger}\)
       • 例：\((\boldsymbol{A}^\mathrm{H}\boldsymbol{A})^\dagger=\boldsymbol{A}^\dagger(\boldsymbol{A}^\mathrm{H})^\dagger, (\boldsymbol{A}\boldsymbol{A}^\mathrm{H})^\dagger=(\boldsymbol{A}^\mathrm{H})^\dagger \boldsymbol{A}^\dagger\)
   • 计算方法
     • 相抵标准型：\(\boldsymbol{A}=\boldsymbol{P}\begin{pmatrix}\boldsymbol{I}_r&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{0}\end{pmatrix}\boldsymbol{Q}\)
       • \(\boldsymbol{A}^-=\boldsymbol{Q}^{-1}\begin{pmatrix}\boldsymbol{I}_r&\boldsymbol{B}\\\boldsymbol{C}&\boldsymbol{D}\end{pmatrix}\boldsymbol{P}^{-1}\)
       • \(\boldsymbol{A}^-_r=\boldsymbol{Q}^{-1}\begin{pmatrix}\boldsymbol{I}_r&\boldsymbol{B}\\\boldsymbol{C}&\boldsymbol{C}\boldsymbol{B}\end{pmatrix}\boldsymbol{P}^{-1}\)
     • 满秩分解：\(\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}, \boldsymbol{F}\in \mathbb{C}^{m\times r}_r, \boldsymbol{G}\in \mathbb{C}^{r\times n}_r\)
       • \(\boldsymbol{G}^{(i)}\boldsymbol{F}^-\in \boldsymbol{A}\{i\}, i=1,2,4\)
       • \(\boldsymbol{G}^-\boldsymbol{F}^{(i)}\in \boldsymbol{A}\{i\}, i=1,2,3\)
       • \(\boldsymbol{G}^-\boldsymbol{F}^\dagger\in \boldsymbol{A}\{1,2,3\}, \boldsymbol{G}^\dagger \boldsymbol{F}^-\in \boldsymbol{A}\{1,2,4\}\)
       • \(\boldsymbol{A}^\dagger=\boldsymbol{G}^\dagger \boldsymbol{F}^{(1,3)}=\boldsymbol{G}^{(1,4)}\boldsymbol{F}^\dagger\)
       • \(\boldsymbol{A}^\dagger=\boldsymbol{G}^\dagger \boldsymbol{F}^\dagger=\boldsymbol{G}^\mathrm{H}(\boldsymbol{G}\boldsymbol{G}^\mathrm{H})^{-1}(\boldsymbol{F}^\mathrm{H}\boldsymbol{F})^{-1}\boldsymbol{F}^\mathrm{H}\)
       • \(\boldsymbol{A}^\dagger=\boldsymbol{G}^\mathrm{H}(\boldsymbol{F}^\mathrm{H}\boldsymbol{A}\boldsymbol{G}^\mathrm{H})^{-1}\boldsymbol{F}^\mathrm{H}\)
     • Zlobec 公式：\(\boldsymbol{A}^\dagger=\boldsymbol{A}^\mathrm{H}(\boldsymbol{A}^\mathrm{H}\boldsymbol{A}\boldsymbol{A}^\mathrm{H})^-\boldsymbol{A}^\mathrm{H}\)
     • Decell 公式：\(\boldsymbol{A}^\dagger=\boldsymbol{A}^\mathrm{H}(\boldsymbol{A}\boldsymbol{A}^\mathrm{H})^-\boldsymbol{A}(\boldsymbol{A}^\mathrm{H}\boldsymbol{A})^-\boldsymbol{A}^\mathrm{H}\)
     • 奇异值分解：\(\boldsymbol{A}^\dag=\boldsymbol{V}\begin{pmatrix}\boldsymbol{\Sigma}_r^{-1}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{0}\end{pmatrix}\boldsymbol{U}^{\mathrm{H}}\)
     • 极限形式：\(\displaystyle \boldsymbol{A}^\dagger=\lim_{\varepsilon\to0+}(\boldsymbol{A}^\mathrm{H}\boldsymbol{A}+\varepsilon \boldsymbol{I})^{-1}\boldsymbol{A}^\mathrm{H}\)
     • 有限迭代算法
     • 特殊矩阵
       • 更新矩阵
       • 分块算法
         • Greville 分块算法及其改进
         • Cline 分块算法
         • Noble 分块算法
       • 半正定矩阵
       • 加边矩阵
10. \(n\) 阶初等矩阵 \(\boldsymbol{E}(\boldsymbol{u},\boldsymbol{v};\sigma):=\boldsymbol{I}_n-\sigma\boldsymbol{u}\boldsymbol{v}^\mathrm{H}\in\mathbb{C}^{n\times n}\)
    • \(\boldsymbol{\lambda}(\boldsymbol{E}(\boldsymbol{u},\boldsymbol{v};\sigma))=\{1-\sigma\boldsymbol{v}^\mathrm{H}\boldsymbol{u},1,\cdots,1\}\)
    • \(\displaystyle \boldsymbol{E}(\boldsymbol{u},\boldsymbol{v};\sigma)^{-1}=\boldsymbol{E}(\boldsymbol{u},\boldsymbol{v};\frac{\sigma}{\sigma\boldsymbol{v}^\mathrm{H}\boldsymbol{u}-1})\)
    • \(\displaystyle \boldsymbol{E}(\boldsymbol{u},\boldsymbol{v};\sigma)\boldsymbol{a}=\boldsymbol{b}\iff \boldsymbol{v}^\mathrm{H}\boldsymbol{a}\neq0,\boldsymbol{u}=\frac{\boldsymbol{a}-\boldsymbol{b}}{\sigma\boldsymbol{v}^\mathrm{H}\boldsymbol{a}}\)
    • 初等变换矩阵
      • 交换 \(i,j\) 行：\(\boldsymbol{E}_{ij}:=\boldsymbol{E}(\boldsymbol{e}_i-\boldsymbol{e}_j,\boldsymbol{e}_i-\boldsymbol{e}_j;1)\)
      • 第 \(i\) 行乘以 \(\alpha\)：\(\boldsymbol{E}_{\alpha i}:=\boldsymbol{E}(\boldsymbol{e}_i,\boldsymbol{e}_i;1-\alpha)\)
      • 第 \(i\) 行乘以 \(\alpha\) 加到第 \(j\) 行：\(\boldsymbol{E}_{\alpha i+j}:=\boldsymbol{E}(\boldsymbol{e}_j,\boldsymbol{e}_i;-\alpha)\)
    • 初等酉阵（Householder 矩阵） \(\boldsymbol{H}(\boldsymbol{w}):=\boldsymbol{E}(\boldsymbol{w},\boldsymbol{w};2),\|\boldsymbol{w}\|_2=1\)
      • 关于 \(\boldsymbol{w}\) 的垂直超平面的反射（镜像）变换矩阵
        • \(\forall \boldsymbol{a}\in\boldsymbol{w}^{\perp},\alpha\in\mathbb{C}:\boldsymbol{H}(\boldsymbol{w})(\boldsymbol{a}+\alpha\boldsymbol{w})=\boldsymbol{a}-\alpha\boldsymbol{w}\)
      • \(\displaystyle \boldsymbol{H}(\boldsymbol{w})\boldsymbol{a}=\boldsymbol{b}\iff \|\boldsymbol{a}\|_2=\|\boldsymbol{b}\|_2,\boldsymbol{w}=\frac{e^{\mathrm{i}\theta}(\boldsymbol{a}-\boldsymbol{b})}{\|\boldsymbol{a}-\boldsymbol{b}\|_2},\theta\in\mathbb{R}\)
11. von Neumann 定理：设 \(\boldsymbol{A}, \boldsymbol{B}\in\mathbb{C}^{m\times n}\) 分别有奇异值 \(\alpha_1\geqslant\cdots\geqslant\alpha_n\geqslant0\) 和 \(\beta_1\geqslant\cdots\geqslant\beta_n\mathbb\geqslant0\)，那么 \(\displaystyle\max_{\boldsymbol{U}\in\mathcal{U}_m,\boldsymbol{V}\in\mathcal{U}_n}\operatorname{\boldsymbol{R}e}\mathrm{tr}(\boldsymbol{U}\boldsymbol{A}\boldsymbol{V}\boldsymbol{B}^\mathrm{H})=\sum_{i=1}^n\alpha_i\beta_i.\)
    • 酉变换：旋转、反射和相位变换的组合
      • 酉矩阵 \(\mathcal{U}_n:=\{\boldsymbol{U}\in\mathbb{C}^{n\times n}_n| \boldsymbol{U}^{\mathrm{H}} \boldsymbol{U}=\boldsymbol{U}\boldsymbol{U}^{\mathrm{H}}=\boldsymbol{I}_n\}\)
        • \(\boldsymbol{B},\boldsymbol{C}\in\mathbb{R}^{n\times n}:\boldsymbol{A}=\boldsymbol{B}+\mathrm{i}\boldsymbol{C}\in\mathcal{U}_n\iff\begin{pmatrix}\boldsymbol{B}&\boldsymbol{C}\\-\boldsymbol{C}&\boldsymbol{B}\end{pmatrix}\in\mathcal{O}_{2n}\)
      • 正交矩阵 \(\mathcal{O}_n\)：\(\boldsymbol{Q}\in\mathbb{R}^{n\times n}_n, \boldsymbol{Q}^\top \boldsymbol{Q}=\boldsymbol{Q}\boldsymbol{Q}^\top=\boldsymbol{I}_n\)
        • 至多 \(\frac{n(n-1)}{2}\) 个 Givens 变换的复合
        • 至多 \(n+1\) 个反射变换的复合
          • 反射矩阵 \(H=H(\boldsymbol{w})\)：\(H\in\mathcal{O}_n,\boldsymbol{\lambda}(H)=\{-1,1,\cdots,1\}\)
        • 旋转矩阵 \(\boldsymbol{R}\)：\(\boldsymbol{R}\in\mathcal{O}_n,|\boldsymbol{R}|=1\)
          • \(n\) 个反射变换的复合
        • 瑕旋转矩阵 \(\boldsymbol{R}\)：\(\boldsymbol{R}\in\mathcal{O}_n,|\boldsymbol{R}|=-1\)
          • 一个旋转变换和一个反射变换的复合
    • 酉矩阵 \(W\in \mathcal{U}_n\) 的列（行）向量标准正交，进而 \(|w_{ii}|\leqslant 1\)
    • \(\forall W\in \mathcal{U}_n,\operatorname{\boldsymbol{R}e}\mathrm{tr}(W\boldsymbol{A})\leqslant\operatorname{\boldsymbol{R}e}\mathrm{tr}(\boldsymbol{A})\iff \boldsymbol{A}\succeq\boldsymbol{0}\)
      • 矩阵经酉变换后迹的实部只减不增当且仅当半正定
    • 序列重排不等式：逆序和 \(\leqslant\) 乱序和 \(\leqslant\) 顺序和
12. 优超关系（\(\boldsymbol{x},\boldsymbol{y}\in\mathbb{R}^n,x_{[1]}\geqslant \cdots\geqslant x_{[n]}\)）
    • 弱优超 \(\boldsymbol{x}\prec_w\boldsymbol{y}\)：\(\displaystyle\sum_{i=1}^k x_{[i]}\leqslant\sum_{i=1}^k y_{[i]}\)
      • \(\boldsymbol{x}\prec_w\boldsymbol{y}\iff \exists\boldsymbol{u}\in\mathbb{R}^n\text{ s.t. } \boldsymbol{x}\leqslant\boldsymbol{u}\) 且 \(\boldsymbol{u}\prec\boldsymbol{y}\)
      • \(\boldsymbol{x},\boldsymbol{y}\geqslant0:\boldsymbol{x}\prec_w\boldsymbol{y}\iff \exists\) 双次随机矩阵 \(\boldsymbol{A}\text{ s.t. } \boldsymbol{x}=\boldsymbol{A}\boldsymbol{y}\)
        • 双次随机矩阵 \(\Gamma_n:=\Big\{\boldsymbol{A}\geqslant 0|\boldsymbol{A}\boldsymbol{1}\leqslant\boldsymbol{1}\text{(行)},\boldsymbol{1}^\top \boldsymbol{A}\leqslant\boldsymbol{1}^\top\text{(列)}\Big\}\)
    • 优超 \(\boldsymbol{x}\prec\boldsymbol{y}\)：\(\boldsymbol{x}\prec_w\boldsymbol{y}\) 且 \(\displaystyle\sum_{i=1}^n x_{i}=\sum_{i=1}^n y_{i}\)
      • Hardy-Littlewood-Polya 定理：\(\boldsymbol{x}\prec\boldsymbol{y}\iff \exists\) 双随机矩阵 \(\boldsymbol{A}\text{ s.t. } \boldsymbol{x}=\boldsymbol{A}\boldsymbol{y}\)
        • 双随机矩阵 \(\Gamma_n:=\Big\{\boldsymbol{A}\geqslant 0|\boldsymbol{A}\boldsymbol{1}=\boldsymbol{1}\text{(行)},\boldsymbol{1}^\top \boldsymbol{A}=\boldsymbol{1}^\top\text{(列)}\Big\}\)
        • 双随机矩阵的方子阵双次随机
    • Krein-Milman 定理：\(K\subset \mathbb{R}^n\) 紧凸 \(\implies\) 极点 \(\operatorname{ex}(K)\neq\emptyset\) 且 \(K=\operatorname{conv}(\operatorname{ex}(K))\)
      • \(\Gamma_n\) 紧凸，\(\operatorname{ex}(\Gamma_n)=PP_n,\Omega_n=\operatorname{conv}(PP_n),PP_n\) 为 \(n\) 阶部分置换矩阵集合
      • Birkhoff 定理：\(\Omega_n\) 紧凸，\(\operatorname{ex}(\Omega_n)=P_n,\Omega_n=\operatorname{conv}(P_n),P_n\) 为 \(n\) 阶置换矩阵集合
    • \(f:\mathbb{R}\to\mathbb{R}\) 凸：\(\boldsymbol{x}\prec\boldsymbol{y}\implies\big(f(x_1),\cdots,f(x_n)\big)\prec_w\big(f(y_1),\cdots,f(y_n)\big)\)
      • Schur 定理：\(\boldsymbol{A}\in\mathcal{H}^n\) 的对角元 \((d_1,\cdots,d_n)\prec(\lambda_1,\cdots,\lambda_n)\)
        • \(\boldsymbol{A}\in\mathcal{H}^n_{+}:\displaystyle\prod_{i=k}^nd_i\geqslant\prod_{i=k}^n\lambda_i\)
          • Hadamard 不等式：\(\displaystyle\prod_{i=1}^nd_i\geqslant\operatorname{det}(\boldsymbol{A})\)（\(k=1\)）
          • Hadamard 不等式：\(\displaystyle \boldsymbol{A}\in \mathbb{C}^{n\times n}:|\operatorname{det}(\boldsymbol{A})|\leqslant\prod_{}^n\|\boldsymbol{c}_i\|_2\)
        • Horn 定理：\((d_1,\cdots,d_n)\prec(\lambda_1,\cdots,\lambda_n)\implies\exist \boldsymbol{A}\in\mathcal{S}^n\) 以 \((d_1,\cdots,d_n)\) 为对角元，以 \((\lambda_1,\cdots,\lambda_n)\) 为特征值
    • \(f:\mathbb{R}\to\mathbb{R}\) 递增且凸：\(\boldsymbol{x}\prec_w\boldsymbol{y}\implies\big(f(x_1),\cdots,f(x_n)\big)\prec_w\big(f(y_1),\cdots,f(y_n)\big)\)
13. 矩阵打洞技巧（分块初等变换）
    • \(\begin{pmatrix}\boldsymbol{I} &\boldsymbol{0}\\-\boldsymbol{V}\boldsymbol{A}^{-1} &\boldsymbol{I}\end{pmatrix}\begin{pmatrix}\boldsymbol{A}&\boldsymbol{U}\\\boldsymbol{V}&\boldsymbol{C}\end{pmatrix}\begin{pmatrix}\boldsymbol{I}&-\boldsymbol{A}^{-1}\boldsymbol{U}\\\boldsymbol{0}&\boldsymbol{I}\end{pmatrix}=\begin{pmatrix}\boldsymbol{A}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{X}/\boldsymbol{A}\end{pmatrix}\)
    • Schur 补 \(\boldsymbol{X}/\boldsymbol{A}:=\boldsymbol{C}-\boldsymbol{V}\boldsymbol{A}^{-1}\boldsymbol{U}\)
    • \(\boldsymbol{A}\succ \boldsymbol{0}: \boldsymbol{X}\succeq \boldsymbol{0}\iff \boldsymbol{X}/\boldsymbol{A}\succeq \boldsymbol{0}\)
14. S-procedure（利用优化对偶理论）；
15. SMW 公式：\(\left( \boldsymbol{A}+\boldsymbol{U}\boldsymbol{C}\boldsymbol{V} \right)^{-1}=\boldsymbol{A}^{-1}-\boldsymbol{A}^{-1}\boldsymbol{U}\left( \boldsymbol{C}^{-1}+\boldsymbol{V}\boldsymbol{A}^{-1}\boldsymbol{U} \right)^{-1}\boldsymbol{V}\boldsymbol{A}^{-1}\)；
    • 

矩阵分解

矩阵的满秩分解

• 对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，使用\(\textcolor{blue}{初等行变换}\)将矩阵 \(\boldsymbol{A}\) 分解为列满秩矩阵 \(\boldsymbol{F}\in \mathbb{C}^{n\times r}_r\) 和行满秩矩阵 \(\boldsymbol{G}\in \mathbb{C}^{r\times m}_r\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{F}\boldsymbol{G}\)；
  • 满秩分解一定存在但不唯一，因为 \(\boldsymbol{A}=(\boldsymbol{F}\boldsymbol{D})(\boldsymbol{D}^{-1}\boldsymbol{G})\)，其中 \(\boldsymbol{D}\in \mathbb{C}^{r\times r}_r\)。
  • 相抵标准型：取 \(\boldsymbol{P}=\left( \boldsymbol{F},\boldsymbol{F}' \right)\in \mathbb{C}^{n\times n}_n, \boldsymbol{Q}=\begin{pmatrix}\boldsymbol{G}\\\boldsymbol{G}'\end{pmatrix}\in \mathbb{C}^{m\times m}_m\)，则 \(\boldsymbol{A}=\boldsymbol{P}\begin{pmatrix}\boldsymbol{I}_r&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{0}\end{pmatrix}\boldsymbol{Q}\)。
  • 算法：经初等行变换化 \(\boldsymbol{A}\) 为（简化）行阶梯型矩阵
• 应用：计算广义逆，解线性方程组

矩阵的三角分解

• LU（Doolittle）分解：对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，使用\(\textcolor{blue}{初等行变换}\)将矩阵 \(\boldsymbol{A}\) 分解为单位下三角型矩阵 \(\boldsymbol{L}\in \mathbb{C}^{n\times n}_n\) 和上三角型矩阵 \(\boldsymbol{U}\in\mathbb{C}^{n\times m}_r\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{U}\)；
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，则存在行置换阵 \(\boldsymbol{P}\in \mathbb{C}^{n\times n}_n\)（左）和列置换阵 \(\boldsymbol{Q}\in \mathbb{C}^{m\times m}_m\)（右）使得 \(\boldsymbol{P}\boldsymbol{A}\boldsymbol{Q}=\boldsymbol{L}\boldsymbol{U}=\begin{pmatrix} \boldsymbol{L}_r&\boldsymbol{0}\\ \boldsymbol{C}_3&\boldsymbol{L}_4\end{pmatrix}\begin{pmatrix} \boldsymbol{U}_r&\boldsymbol{U}_r\boldsymbol{B}\\ \boldsymbol{0}&\boldsymbol{0} \end{pmatrix}=\begin{pmatrix} \boldsymbol{L}_r\\ \boldsymbol{C}_3\end{pmatrix}\begin{pmatrix} \boldsymbol{U}_r&\boldsymbol{U}_r\boldsymbol{B}\end{pmatrix}\)。
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，如果矩阵 \(\boldsymbol{A}\) 的前 \(r\) 阶顺序主子式 \(d_k\neq 0, k=1,2,\cdots,r\)，那么存在 LU 分解 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{U}=\begin{pmatrix} \boldsymbol{L}_r&\boldsymbol{0}\\ \boldsymbol{C}_3&\boldsymbol{L}_4\end{pmatrix}\begin{pmatrix} \boldsymbol{U}_r&\boldsymbol{U}_r\boldsymbol{B}\\ \boldsymbol{0}&\boldsymbol{0} \end{pmatrix}=\begin{pmatrix} \boldsymbol{L}_r\\ \boldsymbol{C}_3\end{pmatrix}\begin{pmatrix} \boldsymbol{U}_r&\boldsymbol{U}_r\boldsymbol{B}\end{pmatrix}\)（不一定唯一）。
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}\)，那么 \(\boldsymbol{A}\) 的 LU 分解存在且唯一 \(\iff\) 其前 \(n-1\) 阶顺序主子式 \(d_k\neq 0, k=1,2,\cdots,n-1\)。
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_n\)，则存在行置换阵 \(\boldsymbol{P}\in \mathbb{C}^{n\times n}_n\)，使得 \(\boldsymbol{P}\boldsymbol{A}=\boldsymbol{L}\boldsymbol{U}\)。
  • 算法：Gauss 消去法（经初等行变换化 \(\boldsymbol{A}\) 为行阶梯型矩阵），（选主元）直接递推法
• LDU* 分解：将上三角型矩阵 \(\boldsymbol{U}\) 分解为对角矩阵 \(\boldsymbol{D}\in \mathbb{C}^{n\times n}_r\) 和单位上三角型矩阵 \(\boldsymbol{U}^*\in \mathbb{C}^{n\times m}_r\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{U}=\boldsymbol{L}\boldsymbol{D}\boldsymbol{U}^*\)；
  • 块 LDU 分解：
  \[\begin{align*} \begin{pmatrix}\boldsymbol{A}&\boldsymbol{B}\\\boldsymbol{C}&\boldsymbol{D}\end{pmatrix}&=\begin{pmatrix}\boldsymbol{I}&\boldsymbol{0}\\\boldsymbol{C}\boldsymbol{A}^{-1}&\boldsymbol{I}\end{pmatrix}\begin{pmatrix}\boldsymbol{A}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{D}-\boldsymbol{C}\boldsymbol{A}^{-1}\boldsymbol{B}\end{pmatrix}\begin{pmatrix}\boldsymbol{I}&\boldsymbol{A}^{-1}\boldsymbol{B}\\\boldsymbol{0}&\boldsymbol{I}\end{pmatrix} \end{align*} \]

• L*U*（Crout）分解：记 \(\boldsymbol{L}^*=\boldsymbol{L}\boldsymbol{D}\)，有分解 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{D}\boldsymbol{U}^*=\boldsymbol{L}^*\boldsymbol{U}^*\)；
• Cholesky 分解（Hermite 三角分解）：对于 \(\boldsymbol{A}\in \mathcal{H}^n_{++}\)，有唯一的 LU 分解 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{D}\boldsymbol{U}^*\)，由于 \(\boldsymbol{A}^\mathrm{H}=(\boldsymbol{L}\boldsymbol{D}\boldsymbol{U}^*)^\mathrm{H}=(\boldsymbol{U}^*)^\mathrm{H}\boldsymbol{D}\boldsymbol{L}^\mathrm{H}=\boldsymbol{A}=\boldsymbol{L}\boldsymbol{D}\boldsymbol{U}^*\) ，有 \(\boldsymbol{U}^*=\boldsymbol{L}^\mathrm{H}\)，进而有 \(\boldsymbol{A}=\boldsymbol{L}\boldsymbol{D}\boldsymbol{L}^\mathrm{H}=\boldsymbol{L}\boldsymbol{D}^{1/2}\boldsymbol{D}^{1/2}\boldsymbol{L}^\mathrm{H}:= \boldsymbol{T}\boldsymbol{T}^\mathrm{H}\)，其中 \(\boldsymbol{T}=\boldsymbol{L}\boldsymbol{D}^{1/2}\) 为下三角型矩阵；
  • 设 \(\boldsymbol{A}\in \mathcal{H}^n_{++}\)，如果规定下三角型矩阵的对角元素均取正，那么 Cholesky 分解存在且唯一。
  • 设 \(\boldsymbol{A}\in \mathcal{H}^n_{+}\)，如果允许下三角型矩阵的对角元素取零，那么 Cholesky 分解存在。
  • 算法：直接递推算法，顺序 Cholesky 分解算法（平方根分解算法）
• 应用：行列式计算，回代法解线性方程组

矩阵的酉三角分解

• QR 分解：对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，使用\(\textcolor{blue}{酉变换}\)将矩阵 \(\boldsymbol{A}\) 分解为酉矩阵 \(\boldsymbol{Q}\in \mathcal{U}_n\) 和上三角型矩阵 \(\boldsymbol{R}\in \mathbb{C}^{n\times m}_r\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{R}\)；
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，则存在列置换阵 \(\boldsymbol{P}\in \mathbb{C}^{n\times n}_n\) 使得 \(\boldsymbol{A}\boldsymbol{P}=\boldsymbol{Q}\boldsymbol{R}=\begin{pmatrix} \boldsymbol{Q}_r&\boldsymbol{Q}_2\\ \boldsymbol{Q}_3&\boldsymbol{Q}_4\end{pmatrix}\begin{pmatrix} \boldsymbol{R}_r&\boldsymbol{R}_r\boldsymbol{B}\\ \boldsymbol{0}&\boldsymbol{0}\end{pmatrix}==\begin{pmatrix} \boldsymbol{Q}_r\\ \boldsymbol{Q}_3\end{pmatrix}\begin{pmatrix}\boldsymbol{R}_r&\boldsymbol{R}_r\boldsymbol{B}\end{pmatrix}\)。
  • 设 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_m\)（\(m\leqslant n\)），则 \(\boldsymbol{A}\) 可以分解为 \(\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{R}\)，其中 \(\boldsymbol{Q}\in\mathbb{C}^{n\times m}\) 标准列正交（即 \(\boldsymbol{Q}^\mathrm{H}\boldsymbol{Q}=\boldsymbol{I}_m\)），\(\boldsymbol{R}\) 为 \(m\) 阶上三角型矩阵；如果规定 \(\boldsymbol{R}\) 的对角元素取正，那么分解式唯一。
  • 算法：Householder 变换法，Givens 变换法，Gram-Schmidt 正交化方法，修正的 Gram-Schmidt 正交化算法（MGS 算法）
• 应用：行列式计算，回代法解线性方程

基于特征值（奇异值）的分解

• Schur 分解：对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\)，使用\(\textcolor{blue}{酉相似变换}\)将矩阵 \(\boldsymbol{A}\) 分解为酉矩阵 \(\boldsymbol{U}\in \mathcal{U}_n\)、Schur 标准型 \(\boldsymbol{R}\in\mathbb{C}^{n\times n}_r\) 和 \(\boldsymbol{U}^\mathrm{H}\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{U}\boldsymbol{R}\boldsymbol{U}^\mathrm{H}\)，其中 \(\boldsymbol{R}\) 是以 \(\boldsymbol{A}\) 的特征值为对角元的上三角型矩阵；
  • \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\) 可酉相似对角化（即 \(\boldsymbol{R}\) 为对角矩阵）\(\iff \boldsymbol{A}\) 为正规矩阵（\(\boldsymbol{A}\boldsymbol{A}^\mathrm{H}=\boldsymbol{A}^\mathrm{H}\boldsymbol{A}\)）\(\iff\forall\boldsymbol{x}\in\mathbb{C}^n: \|\boldsymbol{A}\boldsymbol{x}\|_2=\|\boldsymbol{A}^\mathrm{H}\boldsymbol{x}\|_2\)
    • \(\boldsymbol{R}\) 为实对角矩阵 \(\iff \boldsymbol{A}\) 为 Hermite 矩阵（\(\boldsymbol{A}^\mathrm{H}=\boldsymbol{A}\)）\(\iff \boldsymbol{A}\) 正规且 \(\boldsymbol{\lambda}(\boldsymbol{A})\subseteq \mathbb{R}\)
    • \(\boldsymbol{R}\) 为纯虚对角矩阵 \(\iff \boldsymbol{A}\) 为斜 Hermite 矩阵（\(\boldsymbol{A}^\mathrm{H}=-\boldsymbol{A}\)）
    • \(\boldsymbol{R}\) 对角元模为 \(1\iff \boldsymbol{A}\) 为酉矩阵（\(\boldsymbol{A}^\mathrm{H}\boldsymbol{A}=\boldsymbol{A}\boldsymbol{A}^\mathrm{H}=\boldsymbol{I}_n\)）\(\iff \boldsymbol{A}\) 正规且 \(|\lambda(\boldsymbol{A})|=1\)
  • Gerschgorin 圆盘第一定理：\(\displaystyle\forall \lambda\in\boldsymbol{\lambda}(\boldsymbol{A}):\lambda\in\cup_i G_i\)
    • \(\displaystyle G_i=\{z\in\mathbb{C}\mid | z-a_{ii}|\leqslant \boldsymbol{R}_i=\sum_{j=1,j\neq i}^n |a_{ij}|\}\)
  • Gerschgorin 圆盘第二定理：由 \(k\) 个盖尔圆构成的连通部分恰好包含 \(k\) 个特征值（记重数）
• Jordan 分解：对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\)，使用\(\textcolor{blue}{相似变换}\)将矩阵 \(\boldsymbol{A}\) 分解为非奇异矩阵 \(\boldsymbol{P}\in \mathbb{C}^{n\times n}_n\)、Jordan 标准型 \(\boldsymbol{J}\in\mathbb{C}^{n\times n}_r\) 和 \(\boldsymbol{P}^{-1}\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{P}\boldsymbol{J}\boldsymbol{P}^{-1}\)，其中 \(\boldsymbol{J}=\operatorname{diag}\Big( \boldsymbol{J}_{r_1}(\lambda_1), \cdots, \boldsymbol{J}_{r_k}(\lambda_k)\Big)\)，\(\boldsymbol{J}_{s}(\lambda)=\begin{pmatrix}\lambda&1&&&\\&\lambda&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&\lambda\end{pmatrix}_{s\times s}\)；
  • \(\boldsymbol{A}\) 可分解为两个对称阵的乘积：\(\boldsymbol{A}=\boldsymbol{P}\boldsymbol{J}\boldsymbol{P}^{-1}=\boldsymbol{P}\boldsymbol{S}_{1}\boldsymbol{S}_{2}\boldsymbol{P}^{-1}=(\boldsymbol{P}\boldsymbol{S}_{1}\boldsymbol{P}^{\top})\Big((\boldsymbol{P}^{-1})^{\top}\boldsymbol{S}_{2}\boldsymbol{P}^{-1}\Big)\)，其中 \(\boldsymbol{J}=\boldsymbol{S}_1\boldsymbol{S}_2,\boldsymbol{S}_1^\top=\boldsymbol{S}_1,\boldsymbol{S}_2^\top=\boldsymbol{S}_2\)
    • \(\boldsymbol{J}_{s}(\lambda)=\Big( \boldsymbol{J}_{s}(\lambda)\boldsymbol{K}_s \Big)\boldsymbol{K}_s\)，其中 \(\boldsymbol{K}_s=\boldsymbol{K}_s^\top=\boldsymbol{K}_s^{-1}\) 为反序矩阵。
    • \(\boldsymbol{J}_{s}(\lambda)^\top=\boldsymbol{K}_s\boldsymbol{J}_{s}(\lambda)\boldsymbol{K}_s^{-1}\)
  • Jordan-Chevalley 分解存在且唯一：\(\boldsymbol{A}=\boldsymbol{B}+\boldsymbol{C}\)，其中 \(\boldsymbol{B}\) 单纯，\(\boldsymbol{C}\) 幂零，\(\boldsymbol{B}\boldsymbol{C}=\boldsymbol{C}\boldsymbol{B}\)
    • \(\boldsymbol{B},\boldsymbol{C}\) 均可表示为 \(\boldsymbol{A}\) 的多项式
    • \(\boldsymbol{A}_1,\cdots,\boldsymbol{A}_k\in\mathbb{R}^{n\times n}\) 两两可交换 \(\implies\operatorname{det}(\sum_{i=1}^k\boldsymbol{A}_i^2)\geqslant 0\)
  • 准素分解：设 \(\sigma\in\mathcal{L}(\boldsymbol{V}),\operatorname{dim}\boldsymbol{V}=n,\tau=\sigma-\lambda_i \operatorname{id}\)，且特征多项式 \(f_\sigma(t)=(t-\lambda_1)^{n_1}\cdots(t-\lambda_s)^{n_s}\)（\(s\) 个相异特征值），那么 \(\boldsymbol{V}=\mathcal{N}\Big(f_\sigma(\sigma)\Big)=\overset{s}{\underset{i=1}{\oplus}}\mathcal{N}\Big((\sigma-\lambda_i \operatorname{id})^{n_i}\Big)=\overset{s}{\underset{i=1}{\oplus}}\mathcal{N}(\tau_i^{n_i})\)。
    • \(\tau\) 的不变子空间 \(\boldsymbol{E}\)：\(\forall \boldsymbol{x}\in \boldsymbol{E}: \tau\boldsymbol{x}\in \boldsymbol{E}\)
      • \(\mathcal{R}(\sigma)=\{\sigma\boldsymbol{x}|\boldsymbol{x}\in \boldsymbol{V}\}\)
      • \(\mathcal{N}(\tau)=\{\boldsymbol{x}\in \boldsymbol{V}|\tau\boldsymbol{x}=\boldsymbol{0}\}\)
      • 广义特征子空间（根子空间）：\(\boldsymbol{R}_{\lambda_i}:=\boldsymbol{V}_i^{m_i}\)
        • 特征子空间：\(\boldsymbol{V}_{\lambda_i}:=\boldsymbol{V}_i^{1}\)
        • \(\boldsymbol{V}_i^k:=\mathcal{N}(\tau_i^k),d_{ik}:=\operatorname{dim}\boldsymbol{V}_i^k\)
        • \(\{\boldsymbol{0}\}=\boldsymbol{V}_i^0\subsetneq \boldsymbol{V}_i^1\subsetneq\cdots\subsetneq \boldsymbol{V}_i^{m_i}=\cdots=\boldsymbol{V}_i^{n_i}\)
          • \(0=d_{i0}<d_{i1}<d_{i2}<\cdots<d_{im_i}=\cdots=d_{in_i}=n_i\)
          • \(f_\sigma(t)=f_1(t)\cdots f_s(t)\) 且 \(f_1(t),\cdots, f_s(t)\) 两两互素\(\implies \operatorname{dim}\mathcal{N}(f_i(\sigma))=\operatorname{deg}f_i(t)\)
      • 设 \(\boldsymbol{V}=\overset{k}{\underset{i=1}{\oplus}}\boldsymbol{V}_i, \boldsymbol{V}_i\) 为 \(\sigma\) 的不变子空间，那么存在基使得 \(\sigma\) 在该基下表示矩阵为分块对角阵 \(\operatorname{diag}(\boldsymbol{A}_1,\cdots,\boldsymbol{A}_k)\)，其中 \(\boldsymbol{A}_i\) 为 \(\sigma|_{\boldsymbol{V}_i}\) 的表示矩阵。
        • \(\mu_{i(k+1)}:=d_{i(k+1)}-d_{i(k)}=\operatorname{dim}\Big(\mathcal{R}(\tau_i^k)\cap \boldsymbol{V}_{\lambda_i}\Big)\) 单调不增
          • \(\displaystyle n_i=\sum_{k=1}^{m_i}\mu_{ik},\ \boldsymbol{d}\) 与 \(\boldsymbol{\mu}\) 相互唯一确定
        • \((\mu_{i1},\cdots,\mu_{im_i})\) 的 Young 图（\(m_{i}\times\mu_{i1}\)）中填入的 \(n_i\) 个向量线性无关，从而构成 \(\boldsymbol{R}_{\lambda_i}\) 的一组基
          • \(\mathcal{R}(\tau_i^{m_i-1})\cap \boldsymbol{V}_{\lambda_i}\subset\cdots\subset\mathcal{R}(\tau_i^1)\cap \boldsymbol{V}_{\lambda_i}\subset\mathcal{R}(\tau_i^0)\cap \boldsymbol{V}_{\lambda_i}= \boldsymbol{V}_{\lambda_i}\)
          • 第 \(1\) 行填入一组由上述包含子空间的基逐步扩充而成的特征子空间 \(\boldsymbol{V}_{\lambda_i}\) 的基：\((\tau_i^{m_i-1}\boldsymbol{\eta}_{i1},\cdots,\boldsymbol{\eta}_{i\mu_{i1}})\)
          • 第 \(k\) 列填入 \(\boldsymbol{\eta}_{ik}\) 生成的关于 \(\lambda_i\) 的广义特征向量链，生成一个 \(\sigma\) 的不变子空间 \(W_{ik}\)
          • \(W_{ik}=\operatorname{span}(\tau_i^{\operatorname{dim}W_{ik}-1}\boldsymbol{\eta}_{ik},\cdots,\boldsymbol{\eta}_{ik})\) 为关于 \(\tau_i\) 的循环子空间
          • \(\sharp\{1\leqslant k\leqslant\mu_{i1}:\operatorname{dim}W_{ik}=r_{ij}\}=\mu_{ij}-\mu_{i(j+1)}\)
        • 准素循环分解：\(\boldsymbol{V}=\overset{s}{\underset{i=1}{\oplus}}\boldsymbol{R}_{\lambda_i}=\overset{s}{\underset{i=1}{\oplus}}\left( \overset{\mu_{i1}}{\underset{k=1}{\oplus}}W_{ik} \right)\)
        • \(\sigma|_{\boldsymbol{R}_{\lambda_i}}\) 在 Young 图对应基下的表示矩阵为 \(\operatorname{diag}\Big(\boldsymbol{J}_{m_i}(\lambda_i), \cdots, \boldsymbol{J}_{\operatorname{dim}W_{i\mu_{i1}}}(\lambda_i)\Big)\)
    • 设 \(\sigma\) 在一组基下对应矩阵为 \(\boldsymbol{A}\)，那么 \(d_{ik}=\operatorname{dim}\mathcal{N}\Big((\boldsymbol{A}-\lambda_i \boldsymbol{I}_n)^k\Big)\)
      • \(f_\sigma(t)=|\boldsymbol{A}-t\boldsymbol{I}_n|=(t-\lambda_1)^{n_1}\cdots(t-\lambda_s)^{n_s}\)
      • Hamilton-Caylay 定理：\(f_\sigma(\boldsymbol{A})=\boldsymbol{0}\)
      • \(\lambda_i\) 的几何重数 \(g_{\lambda_i}:=d_{i1}=\mu_{i1}=\) Young 图列数 \(=\lambda_i\) 对应 Jordan 块的个数
      • \(\lambda_i\) 的代数重数 \(a_{\lambda_i}:=n_i=\lambda_i\) 对应 Jordan 块的阶数和
      • 极小多项式 \(m(t)=(t-\lambda_1)^{m_1}\cdots(t-\lambda_s)^{m_s}\)
        • 以 \(\boldsymbol{A}\) 为根的次数最小的非零首一多项式（唯一）
        • \(m_i=\) Young 图行数 \(=\lambda_i\) 对应 Jordan 块的最大阶数
        • \(g(\boldsymbol{A})=\boldsymbol{0}\implies g(\lambda_i)=0\)
          • \(m(t)|g(t), \ m(t)|f_\sigma(t)\)
        • 分块对角阵的极小多项式等于各对角块极小多项式的最小公倍式
  • \(\boldsymbol{A}\sim \boldsymbol{B}\iff \lambda\) 矩阵 \(\lambda \boldsymbol{I}_n-\boldsymbol{A}\cong\lambda \boldsymbol{I}_n-\boldsymbol{B}\iff\) 行列式因子相同 \(\iff\) 不变因子相同 \(\iff\) 初等因子相同
    • \(\boldsymbol{A}(\lambda)\) 的相抵标准型：\(\operatorname{diag}\Big(d_1(\lambda),\cdots,d_r(\lambda), 0,\cdots,0\Big)\)，其中 \(d_i(\lambda)\) 非零首一且 \(d_i(\lambda)|d_{i+1}(\lambda)\)
      • \(\boldsymbol{A}(\lambda)\) 可逆 \(\iff\) 行列式为非零常数 \(\iff\) 可表示为有限个初等 \(\lambda\) 矩阵之积 \(\implies r=n\)
      • \(\lambda \boldsymbol{I}_n-\boldsymbol{A}\) 的相抵标准型：\(\operatorname{diag}\Big(1,\cdots,1,d_1(\lambda),\cdots,d_m(\lambda)\Big)\)，其中 \(d_i(\lambda)\) 非零首一且 \(d_i(\lambda)|d_{i+1}(\lambda)\)
        • \(|\lambda \boldsymbol{I}_n-\boldsymbol{A}|=d_1(\lambda)\cdots d_m(\lambda)\)
        • 极小多项式 \(m(\lambda)=d_m(\lambda)\)
    • \(i\) 阶行列式因子 \(D_i(\lambda)\)： \(\boldsymbol{A}(\lambda)\) 的所有 \(i\) 阶子式的首一最大公因式
      • \(D_i(\lambda)|D_{i+1}(\lambda)\)
    • \(i\) 阶不变因子 \(g_i(\lambda):=D_i(\lambda)/D_{i-1}(\lambda),g_1(\lambda)=D_1(\lambda)\)
      • 相抵标准型不变因子：\(d_1(\lambda),\cdots,d_r(\lambda)\)
    • \(\boldsymbol{A}\) 的有理标准型（Frobenius 标准型）：\(\boldsymbol{F}=\operatorname{diag}(\boldsymbol{F}_1,\cdots,\boldsymbol{F}_m)\)
      • \(\lambda \boldsymbol{I}_n-\boldsymbol{A}\) 的不变因子：\(1,\cdots,1,d_1(\lambda),\cdots,d_m(\lambda)\)
      • \(d_i(\lambda)=\lambda^{t_i}+a_{i1}\lambda^{t_i-1}+\cdots+a_{it_i}\) 对应 \(\boldsymbol{F}_i=\begin{pmatrix}\boldsymbol{0}&\boldsymbol{I}_{t_i-1} \\ -a_{it_i}&-\boldsymbol{a}\end{pmatrix},\boldsymbol{a}=(a_{i(t_i-1)},a_{i(t_i-2)},\cdots,a_{i1})\)
      • \(\boldsymbol{F}_i\) 的行列式因子和不变因子为 \(1,\cdots,1,d_i(\lambda)\)
      • \(\boldsymbol{F}_i\) 的极小多项式为 \(d_i(\lambda)\)
    • \(\boldsymbol{A}\) 在数域 \(\mathbb{F}\) 上的初等因子：对非常数不变因子在数域 \(\mathbb{F}\) 上进行不可约因式分解
      • \(\boldsymbol{A}\) 的 Jordan 标准型：\(\boldsymbol{J}=\operatorname{diag}(\boldsymbol{J}_1,\cdots,\boldsymbol{J}_k)\)
        • \(\mathbb{C}\) 上初等因子 \((\lambda-\lambda_1)^{r_1},\cdots,(\lambda-\lambda_k)^{r_k}\) 分别对应 Jordan 块 \(\boldsymbol{J}_1,\cdots,\boldsymbol{J}_k\)
        • \(\boldsymbol{J}_i\) 的初等因子为 \((\lambda-\lambda_i)^{r_i}\)
    • 数域 \(\mathbb{F}\subset\mathbb{K}:\boldsymbol{A}\overset{\mathbb{F}}\sim \boldsymbol{B}\iff \boldsymbol{A}\overset{\mathbb{K}}\sim \boldsymbol{B}\)
      • 矩阵相似关系在基域扩张下不变
  • \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\) 可相似对角化（单纯矩阵）\(\iff \mathbb{C}^n=\overset{k}{\underset{i=1}{\oplus}}\boldsymbol{V}_{\lambda_i}\iff \boldsymbol{A}\) 有 \(n\) 个线性无关的特征向量 \(\iff g_{\lambda_i}=a_{\lambda_i}\iff\) 极小多项式无重根 \(\iff\) 初等因子次数均为 \(1\)
  • 应用：矩阵函数定义及计算
• 特征值分解：对于可相似对角化矩阵 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\)，使用\(\textcolor{blue}{相似变换}\)将矩阵 \(\boldsymbol{A}\) 分解为非奇异矩阵 \(\boldsymbol{P}\in \mathbb{C}^{n\times n}_n\)、对角矩阵 \(\boldsymbol{\Lambda} \in\mathbb{C}^{n\times n}_r\) 和 \(\boldsymbol{P}^{-1}\) 的乘积，即 \(\boldsymbol{A}=\boldsymbol{P}\boldsymbol{\Lambda} \boldsymbol{P}^{-1}\)，其中 \(\boldsymbol{P}=( \boldsymbol{u}_1,\cdots, \boldsymbol{u}_n)\)，\(\boldsymbol{u}_i\) 为特征值 \(\lambda_i\) 对应的特征向量；
  • 设正规矩阵 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\) 有 \(s\) 个相异特征值，那么谱分解 \(\displaystyle \boldsymbol{A}=\sum_{i=1}^s \lambda_i \boldsymbol{E}_i\) 存在且唯一，其中谱族 \(\boldsymbol{E}_1,\cdots,\boldsymbol{E}_s\) 满足 \(\sum_{i=1}^s \boldsymbol{E}_i=\boldsymbol{I}_n,\boldsymbol{E}_i\boldsymbol{E}_j=\delta_{ij}\boldsymbol{E}_i\)。
    • \(\boldsymbol{E}_i=\boldsymbol{P}_{\boldsymbol{V}_{\lambda_i}}\)
    • \(\boldsymbol{A}\boldsymbol{E}_i=\boldsymbol{E}_i\boldsymbol{A}=\lambda_i \boldsymbol{E}_i\)
  • 对于正规矩阵的酉相似特征值分解 \(\boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Lambda} \boldsymbol{U}^\mathrm{H}\)，如果规定 \(\boldsymbol{\Lambda}\) 中特征值按顺序排列，那么分解式的不唯一性来自于各特征值对应的特征向量取法，对于 \(n_i\) 重特征值 \(\lambda_i\)，其特征向量集 \(\mathcal{U}_i\) 可取为 \((\boldsymbol{u}^i_{1},\cdots,\boldsymbol{u}^i_{n_{i}})\boldsymbol{Q}_{n_i}\)，其中 \(\boldsymbol{Q}_{n_i}\in \mathcal{U}_{n_i}\)。
  • \(\boldsymbol{A}\in \mathbb{R}^{n\times n}_r\) 可正交相似对角化\(\iff \boldsymbol{A}\) 为实对称矩阵
  • 可相似对角化的同阶方阵 \(\boldsymbol{A}, \boldsymbol{B}\) 可同时相似对角化\(\iff \boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}\boldsymbol{A}\)
  • 实对称矩阵 \(\boldsymbol{A}, \boldsymbol{B}\) 可同时正交相似对角化\(\iff \boldsymbol{A}\boldsymbol{B}=\boldsymbol{B}\boldsymbol{A}\)
  • 算法：Jacobi 算法，循环 Jacobi 算法，变限值循环 Jacobi 算法（过关 Jacobi 算法），QR 算法
• 奇异值分解：对于 \(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)，使用\(\textcolor{blue}{酉变换}\)将矩阵 \(\boldsymbol{A}\) 分解为酉矩阵 \(\boldsymbol{U}\in \mathcal{U}_n\)、对角矩阵 \(\boldsymbol{\Sigma} \in\mathbb{C}^{n\times n}_r\) 和酉矩阵 \(\boldsymbol{V}\in \mathcal{U}_n\) 的乘积，即 \(\displaystyle \boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^\mathrm{H}=\sum_{i=1}^r \sigma_i \boldsymbol{u}_i \boldsymbol{v}_i^\mathrm{H}\)，其中 \(\boldsymbol{u}_i, \boldsymbol{v}_i\) 为奇异值 \(\sigma_i:=\sqrt{\lambda_i(\boldsymbol{A}\boldsymbol{A}^\mathrm{H})}=\sqrt{\lambda_i(\boldsymbol{A}^\mathrm{H}\boldsymbol{A})}\) 对应的左、右奇异向量（矩阵 \(\boldsymbol{A}\boldsymbol{A}^\mathrm{H}, \boldsymbol{A}^\mathrm{H}\boldsymbol{A}\) 的特征向量）；
  • 如果规定 \(\boldsymbol{\Sigma}\) 中奇异值按顺序排列，那么分解式的不唯一性来自于各奇异值对应的左右奇异向量取法，即 \(\displaystyle \boldsymbol{A}=\sum_{i=1}^s \sigma_i \boldsymbol{U}_i \boldsymbol{Q}_{n_i} (\boldsymbol{V}_i \boldsymbol{Q}_{n_i})^\mathrm{H}\)，其中 \(s\) 为相异奇异值的个数，\(\boldsymbol{Q}_{n_i}\in \mathcal{U}_{n_i}\)。
  • 设 \(\boldsymbol{A}^H\boldsymbol{A}=\boldsymbol{P}=\begin{pmatrix}\boldsymbol{U}_1, \boldsymbol{U}_2\end{pmatrix}\begin{pmatrix}\boldsymbol{\Sigma}_r&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{0}_{n-r}\end{pmatrix} \begin{pmatrix}\boldsymbol{U}_1^H\\\boldsymbol{U}_2^H\end{pmatrix} \in \mathcal{H}^{n}_{+}\)，其中 \(\boldsymbol{A}\in \mathbb{C}^{p\times n}\)，那么存在标准列正交矩阵 \(\boldsymbol{Q}\in \mathbb{C}^{p\times r}\)（\(\boldsymbol{Q}^H\boldsymbol{Q}=\boldsymbol{I}_r\)） 使得 \(\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{\Sigma}_r^{1/2} \boldsymbol{U}_1^H\)；特别地，\(\boldsymbol{A}^H\boldsymbol{A}=\boldsymbol{B}^H\boldsymbol{B}\iff \boldsymbol{B}_{q\times n}=\boldsymbol{Q}_{q\times p}\boldsymbol{A}_{p\times n}\)。
    • 证明：令 \(\boldsymbol{D}=\operatorname{diag}\left(\boldsymbol{\Sigma}_r^{1/2}, \boldsymbol{I}_{n-r}\right), \boldsymbol{X}=\boldsymbol{A}\boldsymbol{U}\boldsymbol{D}^{-1}:= \left(\boldsymbol{Q}, \boldsymbol{Z}\right)\)，则 \(\boldsymbol{X}^H\boldsymbol{X}=\boldsymbol{D}^{-1}\boldsymbol{U}^H\boldsymbol{A}^H\boldsymbol{A}\boldsymbol{U}\boldsymbol{D}^{-1}=\boldsymbol{D}^{-1}\boldsymbol{U}^H\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{U}^H\boldsymbol{U}\boldsymbol{D}^{-1}=\operatorname{diag}\left(\boldsymbol{I}_r, \boldsymbol{0}_{n-r}\right)\)，对应地，有 \(\boldsymbol{Q}^H\boldsymbol{Q}=\boldsymbol{I}_r, \boldsymbol{Z}^H\boldsymbol{Z}=\boldsymbol{0}_{n-r}\)，进而有 \(\boldsymbol{A}=\boldsymbol{X}\boldsymbol{D}\boldsymbol{U}^H=\left(\boldsymbol{Q}, \boldsymbol{0}\right)\begin{pmatrix}\boldsymbol{\Sigma}_r^{1/2}&\boldsymbol{0}\\\boldsymbol{0}&\boldsymbol{I}_{n-r}\end{pmatrix}\begin{pmatrix}\boldsymbol{U}_1^H\\\boldsymbol{U}_2^H\end{pmatrix}=\boldsymbol{Q}\boldsymbol{\Sigma}_r^{1/2} \boldsymbol{U}_1^H\)。
  • 极分解：设 \(\boldsymbol{A}\in \mathbb{C}^{n\times n}_r\)，则存在 \(\boldsymbol{S}\in\mathcal{U}_n\) 和唯一的半正定矩阵 \(\boldsymbol{P}=\sqrt{\boldsymbol{A}\boldsymbol{A}^\mathrm{H}}\in\mathcal{H}^{n}_{+}\) 使得 \(\boldsymbol{A}=\boldsymbol{P}\boldsymbol{S}\)，且 \(r=n\iff \boldsymbol{S}\) 唯一。
    • \(\boldsymbol{A}=\boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^\mathrm{H}=\left( \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{U}^{\mathrm{H}} \right)\left( \boldsymbol{U}\boldsymbol{V}^\mathrm{H} \right)\)
    • \(z=a+b\mathrm{i}=re^{\mathrm{i}\theta}=\sqrt{a^2+b^2}\left( \cos\theta+\mathrm{i}\sin\theta \right)\in\mathbb{C}\)
    • 推广：\(\boldsymbol{A}\in \mathbb{C}^{n\times m}_r\)
      • \(n<m:\boldsymbol{A}=\boldsymbol{P}\boldsymbol{S},\boldsymbol{P}=\sqrt{\boldsymbol{A}\boldsymbol{A}^\mathrm{H}}\in\mathcal{H}^{n}_{+},\boldsymbol{S}\) 标准行正交
      • \(n>m:\boldsymbol{A}=\boldsymbol{S}\boldsymbol{P},\boldsymbol{P}=\sqrt{\boldsymbol{A}^\mathrm{H}\boldsymbol{A}}\in\mathcal{H}^{m}_{+},\boldsymbol{S}\) 标准列正交
  • 算法：特征值分解法，经 Householder 变换化 \(\boldsymbol{A}\) 为双对角型后进行奇异值分解
  • 应用：计算广义逆（解线性方程组），主成分分析

矩阵求导

• 符号约定：\(\frac{\partial \boxdot}{\partial \boxdot}\) 表示 \(\boxdot\) 相对于另一 \(\boxdot\) 逐分量求偏导后填充在原分量对应位置；
• 各函数分量对各变元分量偏导数的不同组织方式（\(\boldsymbol{f}(\boldsymbol{x}):\mathbb{R}^n\to\mathbb{R}^m\)）
  • 梯度矩阵：\(\nabla_{\boldsymbol{x}}\boldsymbol{f}:=\frac{\partial \boldsymbol{f}^\top}{\partial \boldsymbol{x}}=[\frac{\partial f_1}{\partial\boldsymbol{x}},\cdots, \frac{\partial f_m}{\partial\boldsymbol{x}}]\in\mathbb{R}^{n\times m}\)
    • 分母布局：标量函数梯度形状与分母形状保持一致
    • 内左外右：链式法则从内到外依次相乘
      • \(\frac{\partial\left( \boldsymbol{f}\circ \boldsymbol{g} \right)^\top}{\partial \boldsymbol{x}}=\frac{\partial \boldsymbol{g}^\top}{\partial \boldsymbol{x}}\frac{\partial\left( \boldsymbol{f}\circ \boldsymbol{g} \right)^\top}{\partial \boldsymbol{g}}\)
  • Jacobian 矩阵：\(\boldsymbol{D}_{\boldsymbol{x}}\boldsymbol{f}:=\frac{\partial \boldsymbol{f}}{\partial \boldsymbol{x}^\top}=[\frac{\partial \boldsymbol{f}}{\partial x_1},\cdots, \frac{\partial \boldsymbol{f}}{\partial x_n}]\in\mathbb{R}^{m\times n}\)
• 所有变量均转化为列向量处理
  • 标量 \(x\in\mathbb{R}:n=1\)
  • 矩阵 \(\boldsymbol{X}\in\mathbb{R}^{m\times n}:\operatorname{vec}\boldsymbol{X}\)
    • \(\textcolor{blue}{\nabla_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X}):=\frac{\partial\operatorname{vec}^\top \boldsymbol{F}(\boldsymbol{X})}{\partial\operatorname{vec}\boldsymbol{X}}}=\left( \frac{\partial\operatorname{vec} \boldsymbol{F}(\boldsymbol{X})}{\partial\operatorname{vec}^\top \boldsymbol{X}} \right)^\top=\left( \boldsymbol{D}_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X}) \right)^\top\)
• 常规方法：逐分量求偏导法
• 微分法
  • 辨识规则
    • 矩阵函数 \(\boldsymbol{F}(\boldsymbol{X}):\mathbb{R}^{m\times n}\to\mathbb{R}^{p\times q}\)
      • \(\textcolor{blue}{\mathrm{d}\left( \operatorname{vec}\boldsymbol{F}(\boldsymbol{X}) \right)= \boldsymbol{A}\mathrm{d}\left( \operatorname{vec}\boldsymbol{X} \right)+\boldsymbol{B}\mathrm{d}\left( \operatorname{vec}\boldsymbol{X}^\top \right)\iff\nabla_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=\boldsymbol{A}^\top+\boldsymbol{K}_{nm}\boldsymbol{B}^\top}\)
      • \(\mathrm{d}\left( \boldsymbol{F}(\boldsymbol{X}) \right)= \boldsymbol{A}\left( \mathrm{d}\boldsymbol{X} \right)\boldsymbol{B}+\boldsymbol{C}\left( \mathrm{d}\boldsymbol{X}^\top \right)\boldsymbol{D}\iff\nabla_{\boldsymbol{X}}\boldsymbol{F}(\boldsymbol{X})=\left( \boldsymbol{B}\otimes \boldsymbol{A}^\top \right)+\boldsymbol{K}_{nm}\left( \boldsymbol{D}\otimes \boldsymbol{C}^\top \right)\)
    • 标量函数 \(f(\boldsymbol{X})\in\mathbb{R}\)
      • \(\mathrm{d}\left( f(\boldsymbol{X}) \right)= \operatorname{vec}(\boldsymbol{A}^\top)^\top\mathrm{d}\left( \operatorname{vec}\boldsymbol{X} \right)=\operatorname{tr}(\boldsymbol{A}\mathrm{d}\boldsymbol{X})\iff\textcolor{red}{\nabla_{\boldsymbol{X}}f(\boldsymbol{X})=\boldsymbol{A}^\top}\)
      • Hessian 矩阵：\(\textcolor{blue}{H[f(\boldsymbol{X})]:=\frac{\partial^2 f(\boldsymbol{X})}{\partial\operatorname{vec}\boldsymbol{X}\partial\left( \operatorname{vec}\boldsymbol{X} \right)^\top}}=\nabla_{\boldsymbol{X}}\left( \boldsymbol{D}_{\boldsymbol{X}}f(\boldsymbol{X}) \right)\) 对称
      • \(\textcolor{blue}{\mathrm{d}^2f(\boldsymbol{X})=\mathrm{d}(\operatorname{vec}\boldsymbol{X})^\top \boldsymbol{B}\mathrm{d}(\operatorname{vec}\boldsymbol{X})\iff H[f(\boldsymbol{X})]=\left( \boldsymbol{B}^\top+\boldsymbol{B} \right)/2}\)
      • \(\mathrm{d}^2f(\boldsymbol{X})=\operatorname{tr}(\boldsymbol{V}\left( \mathrm{d}\boldsymbol{X} \right)\boldsymbol{U}\left( \mathrm{d}\boldsymbol{X} \right)^\top)\iff H[f(\boldsymbol{X})]=\left( \boldsymbol{U}^\top\otimes \boldsymbol{V}+\boldsymbol{U}\otimes \boldsymbol{V}^\top \right)/2\)
      • \(\mathrm{d}^2f(\boldsymbol{X})=\operatorname{tr}(\boldsymbol{B}\left( \mathrm{d}\boldsymbol{X} \right)\boldsymbol{C}\left( \mathrm{d}\boldsymbol{X} \right))\iff H[f(\boldsymbol{X})]=\boldsymbol{K}_{nm}\left( \boldsymbol{C}^\top\otimes \boldsymbol{B}+\boldsymbol{B}^\top\otimes \boldsymbol{C} \right)/2\)
  • 微分性质
    • \(\mathrm{d}\boldsymbol{A}=\boldsymbol{0}, \mathrm{d}\left( \alpha \boldsymbol{A} \right)=\alpha \mathrm{d}\left( \boldsymbol{A} \right), \mathrm{d}\left( \boldsymbol{X}^\top \right)=\left( \mathrm{d}\boldsymbol{X} \right)^\top\)
    • \(\mathrm{d}\left( \boldsymbol{U}(\boldsymbol{X})\plusmn \boldsymbol{V}(\boldsymbol{X}) \right)=\mathrm{d}\boldsymbol{U}(\boldsymbol{X})\plusmn \mathrm{d}\boldsymbol{V}(\boldsymbol{X})\)
    • \(\mathrm{d}\left( \boldsymbol{U}(\boldsymbol{X})\star \boldsymbol{V}(\boldsymbol{X}) \right)=\mathrm{d}\boldsymbol{U}(\boldsymbol{X}) \star \boldsymbol{V}(\boldsymbol{X})+\boldsymbol{U}(\boldsymbol{X})\star \mathrm{d}\boldsymbol{V}(\boldsymbol{X})\)
      • \(\star\) 可取乘积、Hadamard 积、KKronecker 积
    • \(\mathrm{d}\left( \operatorname{tr}(\boldsymbol{F}(\boldsymbol{X}) \right)=\operatorname{tr}(\mathrm{d}\boldsymbol{F}(\boldsymbol{X}))\)
    • \(\mathrm{d}|\boldsymbol{F}(\boldsymbol{X})|=|\boldsymbol{F}(\boldsymbol{X})|\operatorname{tr}(\boldsymbol{F}(\boldsymbol{X})^{-1}\mathrm{d}\left( \boldsymbol{F}(\boldsymbol{X}) \right))\)
    • \(\mathrm{d}\left( \operatorname{vec}(\boldsymbol{F}(\boldsymbol{X}) \right)=\operatorname{vec}(\mathrm{d}\boldsymbol{F}(\boldsymbol{X}))\)
    • \(\mathrm{d}\left( \boldsymbol{X}^{-1} \right)=-\boldsymbol{X}^{-1}(\mathrm{d}\boldsymbol{X})\boldsymbol{X}^{-1}\)
    • \(\mathrm{d}\left( \boldsymbol{X}^\dag \right)=-\boldsymbol{X}^\dag(\mathrm{d}\boldsymbol{X})\boldsymbol{X}^\dag+\boldsymbol{X}^\dag(\boldsymbol{X}^\dag)^\top\left( \mathrm{d}\boldsymbol{X}^\top \right)(\boldsymbol{I}_m-\boldsymbol{X}\boldsymbol{X}^\dag)+(\boldsymbol{I}_n-\boldsymbol{X}^\dag \boldsymbol{X})\left( \mathrm{d}\boldsymbol{X}^\top \right)(\boldsymbol{X}^\dag)^\top \boldsymbol{X}^\dag\)
      • \(\mathrm{d}\left( \boldsymbol{X}^\dag \boldsymbol{X} \right)=\boldsymbol{X}^\dag\left( \mathrm{d}\boldsymbol{X} \right)\left( \boldsymbol{I}_n-\boldsymbol{X}^\dag \boldsymbol{X} \right)+\left( \boldsymbol{X}^\dag\left( \mathrm{d}\boldsymbol{X} \right)\left( \boldsymbol{I}_n-\boldsymbol{X}^\dag \boldsymbol{X} \right) \right)^\top\)
      • \(\mathrm{d}\left( \boldsymbol{X}\boldsymbol{X}^\dag \right)=\left( \boldsymbol{I}_m-\boldsymbol{X}\boldsymbol{X}^\dag \right)\left( \mathrm{d}\boldsymbol{X} \right)\boldsymbol{X}^\dag+\left( \left( \boldsymbol{I}_m-\boldsymbol{X}\boldsymbol{X}^\dag \right)\left( \mathrm{d}\boldsymbol{X} \right)\boldsymbol{X}^\dag \right)^\top\)