BZOJ2286: [Sdoi2011]消耗战
$n \leq 250000$的树有边权,每次问:使$k$个点无法到达根节点至少要割边权总和多少的边。$k$总和$\leq 500000$。
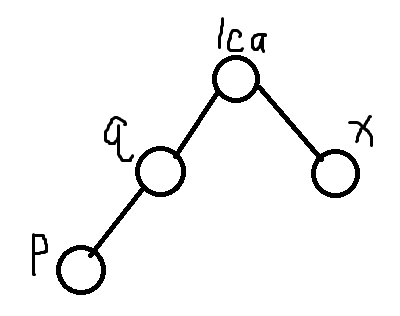
虚树模板。

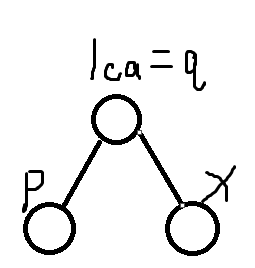

1 //#include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 //#include<math.h> 5 //#include<set> 6 //#include<queue> 7 //#include<bitset> 8 //#include<vector> 9 #include<algorithm> 10 #include<stdlib.h> 11 using namespace std; 12 13 #define LL long long 14 int qread() 15 { 16 char c; int s=0,f=1; while ((c=getchar())<'0' || c>'9') (c=='-') && (f=-1); 17 do s=s*10+c-'0'; while ((c=getchar())>='0' && c<='9'); return s*f; 18 } 19 20 //Pay attention to '-' , LL and double of qread!!!! 21 22 int n,m; 23 #define maxn 250011 24 struct Edge{int to,v,next;}; 25 struct Tree 26 { 27 Edge edge[maxn<<1]; int first[maxn],le; 28 Tree() {le=2;} 29 void in(int x,int y,int v) {Edge &e=edge[le]; e.to=y; e.v=v; e.next=first[x]; first[x]=le++;} 30 void insert(int x,int y,int v) {in(x,y,v); in(y,x,v);} 31 }t,tt; 32 33 int fa[22][maxn],mm[22][maxn],dep[maxn],dfn[maxn],Time=0; 34 void dfs(int x) 35 { 36 dfn[x]=++Time; 37 for (int i=t.first[x];i;i=t.edge[i].next) 38 { 39 Edge &e=t.edge[i]; if (e.to==fa[0][x]) continue; 40 fa[0][e.to]=x; dep[e.to]=dep[x]+1; mm[0][e.to]=e.v; 41 dfs(e.to); 42 } 43 } 44 void makefa() 45 { 46 mm[0][0]=0x3f3f3f3f; 47 for (int j=1;j<=19;j++) 48 for (int i=1;i<=n;i++) 49 mm[j][i]=0x3f3f3f3f; 50 for (int j=1;j<=19;j++) 51 for (int i=1;i<=n;i++) 52 { 53 fa[j][i]=fa[j-1][fa[j-1][i]]; 54 mm[j][i]=min(mm[j-1][i],mm[j-1][fa[j-1][i]]); 55 } 56 } 57 int lca(int x,int y) 58 { 59 if (dep[x]<dep[y]) x^=y^=x^=y; 60 for (int i=19;~i;i--) if (dep[fa[i][x]]>=dep[y]) x=fa[i][x]; 61 if (x==y) return x; 62 for (int i=19;~i;i--) if (fa[i][x]!=fa[i][y]) x=fa[i][x],y=fa[i][y]; 63 return fa[0][x]; 64 } 65 int qmin(int x,int f) 66 { 67 int ans=0x3f3f3f3f; 68 for (int i=19;~i;i--) if (dep[fa[i][x]]>=dep[f]) ans=min(ans,mm[i][x]),x=fa[i][x]; 69 return ans; 70 } 71 72 int kk[maxn],lk,sta[maxn],top,list[maxn],len; bool isk[maxn],intt[maxn]; 73 bool cmp(const int x,const int y) {return dfn[x]<dfn[y];} 74 void play(int x) {if (intt[x]) return; list[++len]=x; intt[x]=1;} 75 void buildtt() 76 { 77 top=0; len=0; 78 for (int i=1;i<=lk;i++) 79 { 80 int x=kk[i]; 81 if (top==0) {sta[++top]=x; continue;} 82 int l=lca(x,sta[top]); 83 while (top>1 && dep[sta[top-1]]>dep[l]) 84 { 85 tt.in(sta[top-1],sta[top],qmin(sta[top],sta[top-1])); 86 play(sta[top]); top--; 87 } 88 if (dep[sta[top]]>dep[l]) 89 { 90 tt.in(l,sta[top],qmin(sta[top],l)); 91 play(sta[top]); top--; 92 } 93 if (top==0 || sta[top]!=l) sta[++top]=l; 94 sta[++top]=x; 95 } 96 while (top>1) 97 { 98 tt.in(sta[top-1],sta[top],qmin(sta[top],sta[top-1])); 99 play(sta[top]); top--; 100 } 101 play(sta[1]); top=0; 102 } 103 104 LL f[maxn][2]; 105 void dp(int x,int v) 106 { 107 if (isk[x]) {f[x][0]=v; f[x][1]=0; return;} 108 f[x][0]=f[x][1]=1e18; 109 LL tot0=0,tot01=0; 110 for (int i=tt.first[x];i;i=tt.edge[i].next) 111 { 112 Edge &e=tt.edge[i]; 113 dp(e.to,e.v); 114 tot0+=f[e.to][0]; tot01+=min(f[e.to][0],f[e.to][1]); 115 } 116 f[x][0]=min(tot0,tot01+(LL)(x==1?1e18:v)); 117 f[x][1]=tot01; 118 } 119 120 void destroytt() 121 { 122 tt.le=2; 123 for (int i=1;i<=len;i++) 124 { 125 int x=list[i]; 126 tt.first[x]=0; 127 intt[x]=0; 128 } 129 } 130 131 int main() 132 { 133 n=qread(); 134 for (int i=1,x,y,v;i<n;i++) 135 { 136 x=qread(); y=qread(); v=qread(); 137 t.insert(x,y,v); 138 } 139 dep[1]=1; dfs(1); 140 makefa(); 141 142 m=qread(); 143 for (int i=1;i<=m;i++) 144 { 145 lk=qread(); bool flag=0; 146 for (int j=1;j<=lk;j++) {kk[j]=qread(); isk[kk[j]]=1; if (kk[j]==1) flag=1;} 147 if (!flag) kk[++lk]=1; 148 sort(kk+1,kk+1+lk,cmp); 149 buildtt(); 150 dp(1,0x3f3f3f3f); 151 printf("%lld\n",f[1][0]); 152 destroytt(); 153 for (int j=1;j<=lk;j++) isk[kk[j]]=0; 154 } 155 return 0; 156 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号