代数方法在图论中的精彩应用
Preface
一直想对GTAC讨论班的一些精彩内容做一次整理,却一直挖不出时间来。昨晚我们在讨论班教室吃披萨,喝果汁,听了一些代数方法在图论中的应用,度过了愉快的平安夜。新的一年(和ddl)快要来了,是时候做个整理了。
由于 eden 上课不做笔记,忘记了一些定理的名字以及来源,再由于时间关系 eden 不能整理得特别详细。所以凑合着看吧 :)
Graham-Pollack theorem
Theorem 1. (Graham-Pollack theorem) 若完全图 \(K_n\) 可以表示为 \(m\) 个互不相交的完全二分图的并,则 \(m\ge n-1\)。
设图 \(K_n\) 的邻接矩阵为 \(A\),那么 \(A=J-I\)(约定 \(J\) 为全 \(1\) 矩阵,\(I\) 为单位矩阵)。
如果 \(K_n\) 的一个子图 \(G\) 是完全二分图,一边的点集为 \(V_1\),另一边的点集为 \(V_2\)。那么该子图的邻接矩阵 \(B\) 满足:\(B_{x,y}=B_{y,x}=1,\forall x\in V_1,y\in V_2\)。所以 \(B\) 可以拆成一个秩一矩阵与它的转置之和:\(B=C^T+C\ (C_{x,y}=1,\forall x\in V_1,y\in V_2)\)。
\(K_n\) 可以拆成 \(m\) 个互不相交的完全二分图的并,所以 \(A\) 可以表示为 \((C_1+\cdots+C_m)^T+(C_1+\cdots+C_m)\),其中 \(C_1,\cdots,C_m\) 都是秩一矩阵。可以推出:
假设 \(m<=n-2\),那么 \(rank(D)\le rank(J)+rank(C_1)\cdots+rank(C_m)=n-1\),
取 \(D\) 的右零空间中的一个非零向量 \(\boldsymbol \alpha\),在 \((1.1)\) 式中左乘 \(\boldsymbol \alpha^T\),右乘 \(\boldsymbol \alpha\),\((1.1)\) 式变为:
这与 \(\boldsymbol \alpha\) 是非零向量矛盾。所以 \(m\ge n-1\)。Q.E.D.
Friendship Theorem
Theorem 2. (Friendship Theorem) 图 \(G=(V,E)\) 中任意两个点 \(a,b\) 有且仅有一个公共邻居,则一定有一个点的度数为 \(n-1\)(\(n=|V|\))。
容易发现,风车状的图是满足定理条件的:
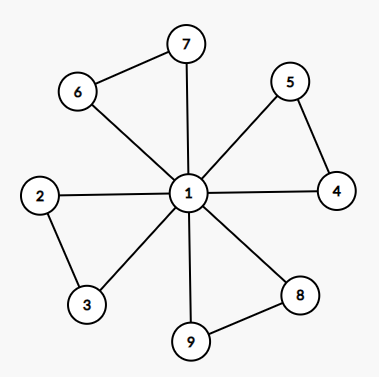
下面先证明:若 \(a,b\) 不相连,则 \(d(a)=d(b)\)(约定 \(d(x)\) 为 \(x\) 的度数)。
设 \(a\) 与 \(b\) 的公共邻居为 \(c\)(\(c\) 存在且唯一),\(a\) 的其他邻居为 \(x_1,\cdots,x_p\),\(b\) 的其他邻居为 \(y_1,\cdots,y_q\)。又 \(a\) 与 \(c\) 有且仅有一个公共邻居,那么不妨设这个公共邻居为 \(x_1\),那么 \(x_2,\cdots,x_p\) 与 \(c\) 都不相连。同理,不妨设 \(b\) 与 \(c\) 的公共邻居为 \(y_1\),那么 \(y_2,\cdots,y_q\) 与 \(c\) 都不相连。还可以推出 \(x_1\) 与 \(y_j(1\le j\le q)\) 都不相连,否则 \(b\) 与 \(x_1\) 的公共邻居就不唯一了。同理,\(y_1\) 与 \(x_i(1\le i\le p)\) 都不相连。
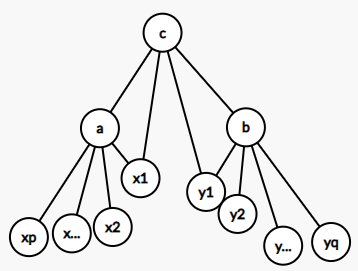
现在考虑 \(x_2,\cdots,x_p\) 与 \(y_2,\cdots,y_q\) 之间的连边。\(a\) 与 \(y_2\) 有公共邻居(不能为 \(c\)),不妨设这个公共邻居为 \(x_2\),那么 \(x_2\) 与 \(y_2\) 相连。再由 \(a\) 与 \(y_2\) 公共邻居的唯一性,\(y_2\) 与其他的 \(x_i(i\neq 2)\) 都不相连,同理 \(x_2\) 与其他的 \(y_j(j\neq 2)\) 都不相连。 用同样的方法继续讨论 \(y_3,x_3,\cdots\)。最终 \(x_2,x_3,\cdots,x_p\) 与 \(y_2,y_3,\cdots,y_q\) 一定能通过连边一一对应,这说明 \(p=q\),\(d(a)=d(b)\)。所以,不相连的点度数一定相等。
回到原定理,令 \(G\) 的补图 \(G'=(V',E')\),则由前面的结论可知,\(d(a)=d(b),\forall (a,b)\in E'\)。\(G'\) 可以拆分为若干个连通分量的并,设它们的点集分别为 \(U_1,U_2,\cdots,U_m\),那么每个点集中,点的度数是相同的,且任意两个点集之间无边相连(在原图 \(G\) 中任意两个点集都互相连满了边)。对 \(m\) 进行讨论:
若 \(m\ge2\),那么 \(V=U_1\cup (U_2\cup \cdots\cup U_k)=U_1\cup V_1\)。当 \(|U_1|>1,|V_1|>1\),取 \(x_1,x_2\in U_1,y_1,y_2\in V_1\),那么 \(y_1,y_2\) 都是 \(x_1,x_2\) 的公共邻居,这与条件矛盾。当 \(|U_1|=1\) 或 \(|V_1|=1\),那么就存在度数为 \(n-1\) 的点,命题成立。
若 \(m=1\),那么图 \(G\) 中所有点度数相同,设每个点度数为 \(k\),可以推得 \(k\) 与 \(n\) 的关系:
\(G\) 的邻接矩阵为 \(A\),\(trace(A)=0\)。由条件“任意两个点 \(a,b\) 有且仅有一个公共邻居”可知,\(A\) 的任意不同的两行点乘为 \(1\)。又有 \(A^T=A\),所以 \(A^2=J+(k-1)I\)。\(J\) 的特征值为 \(n(1重),0(n-1重)\),所以 \(A^2\) 的特征值为 \(n+k-1(=k^2),k-1\),\(A\) 的特征值的绝对值为 \(k(1重),\sqrt{k-1}(n-1重)\)。 \(|trace(A)|=|k+a\sqrt{k-1}|=0,a\in \mathbb{Z}\),\(k\) 只可能为 \(2\)。此时 \(n=3\),\(G\) 为完全图,与 \(m=1\) 矛盾。Q.E.D.
Pyber Theorem (Regular subgraphs of dense graphs)
Theorem 3. (Pyber Theorem) 对任意正整数 \(k\),存在一个常量 \(c_k\),满足:对于充分大的图 \(G=(V,E)\),\(|V|=n,|E|\ge c_kn\log n\),一定存在一个 \(k-regular\) 子图(一个图被称为是 \(k-regular\) 的,当且仅当每个点的度数为 \(k\))。
这个定理的证明需要有 “Chevalley-Warning Theorem” 的铺垫。
Theorem 3.1. (组合零点定理) \(\mathbb{F}\) 为任意一个域,\(S_i\) 为包含于 \(\mathbb{F}\) 的有限集(\(i=1,\cdots,n\)),令 \(f=f(x_1,\cdots,x_n)\) 为多项式环 \(\mathbb{F}[x_1,\cdots,x_n]\) 中的一个多项式。若 \(S_1\times S_2\times \cdots\times S_n \subseteq z(f)\)(\(z(f)\) 表示多项式 \(f\) 的零点集),那么一定存在 \(k_i\in \mathbb{F}[x_1,\cdots,x_n]\)(\(i=1,\cdots,n\)),满足:
其中 \(g_i=\prod_{g\in S_i}(x_i-g)\)。
先将 \(x_1\) 看作主元,多项式 \(f\) 对 \(g_1\) 做带余除法,得到 \(f=h_1g_1+r_1\)。再将 \(x_2\) 看作主元, \(r_1\) 对 \(g_2\) 做带余除法,得到 \(f=h_1g_1+h_2g_2+r_2\)。以此类推,最终可以得到:
其中 \(r_n\) 的任意变量 \(x_i\) 的次数都小于 \(\deg g_i=|S_i|\)。
下面证明 \(r_n\) 是零多项式。
对 \(n\) 归纳。当 \(n=1\) 时显然。\(n>1\) 时,将 \(x_n\) 看作主元,\(r_n=\sum w_ix_n^i\),其中 \(w_i\) 为关于 \(x_1,\cdots,x_{n-1}\) 的多项式。当 \(x_1,\cdots,x_{n-1}\) 分别取定为 \(S_1,\cdots,S_{n-1}\) 中的值后,\(r_n'\) 为关于 \(x_n\) 的一元多项式,且 \(\deg r_n'<|S_n|\)。这说明 \(r_n'\) 总为零多项式,即 \(S_1\times S_2\times \cdots\times S_{n-1} \subseteq z(w_i)\)。由归纳假设,所有 \(w_i\) 都为零多项式。那么 \(r_n\) 也为零多项式。
所以 \(r_n\) 为零多项式。容易证明 \(\deg(k_i)\le \deg f-\deg g_i\),所以可以令 \(k_1=h_1,\cdots,k_n=h_n\)。Q.E.D.
Corollary 3.1.1. 若 \(f\in \mathbb{F}[x_1,\cdots,x_n]\),\(S_1\times S_2\times \cdots\times S_n \subseteq z(f)\),那么 \(f\) 的各单项式中必有一个变量 \(x_i\) 次数小于等于 \(|S_i|\)。
Theorem 3.2. (Chevalley-Warning Theorem) \(\mathbb{F}_q\) 为 \(q\) 元域,\(q=p^k\),\(p\)为素数,\(P_1,P_2,\cdots,P_m\) 为 \(\mathbb{F}_q[x_1,\cdots,x_n]\) 中的多项式,且 \(\sum_{i=1}^n \deg P_i <n\),设 \(V=z(P_1)\cap z(P_2)\cap \cdots \cap z(P_m)\),则 \(|V|\bmod p=0\)。
构造多项式 \(f(x_1,x_2,\cdots,x_n)\):
则当 \(\boldsymbol x\in V\) 时, \(f(\boldsymbol x)=1\);当 \(\boldsymbol x\notin V\) 时,\(\exist j,P_j\neq 0,P_j^{q-1}=1, f(\boldsymbol x)=0\)。所以 \(f\) 为 \(V\) 的特征函数。问题化为证明:
由于 \(\sum_{i=1}^n \deg P_i<n\),我们有 \(\deg f<n(q-1)\),所以 \(f\) 的各个单项式中必有一个变量次数小于 \(q-1\)。对于所有 \(\boldsymbol v=(v_1,v_2,\cdots,v_n)\in V\),构造多项式:
\(g_v(x)\) 是 \(\{\boldsymbol v\}\) 的特征函数,而 \(f\) 为 \(V\) 的特征函数。所以 \(h=f-\sum_{\boldsymbol v\in V}g_v\) 恒等于 \(0\)(\(h\) 不一定是零多项式),即:
由 Corollary 3.1.1 可知,\(h\) 的各个单项式中必有一个变量次数小于 \(q-1\)。\(f\) 已满足此条件,只需考察 \(g_v\) 的各单项式。由 \((3.2.2)\) 式可得, \(g_v\) 中有单项式 \((-1)^n\prod_{i=1}^n x_i^{q-1}\),而 \(\sum_{\boldsymbol v\in V} g_v\) 中不能存在此单项式,所以 \(\sum_{v\in V}(-1)^n=|V|(-1)^n=0(\mathbb{F_q})\)。域 \(\mathbb{F}_q\) 的特征为 \(p\),所以 \(|V| \bmod p=0\)。Q.E.D.
Lemma 3.3. \(p\) 为一素数,\(q=p^k(k\in \mathbb{N})\),图 \(G=(V,E)\),\(d(G)\ge 2q-2\),\(\Delta(G)=2q-1\)(约定 \(d(G)\) 为 \(G\) 中每个点的平均度数,\(\Delta(G)\) 为 \(G\) 中度数最大的点的度数)。则 \(G\) 中存在 \(q-regular\) 子图。
对每条边 \((u,v)\in E\) 分别设定一个变量 \(x_i\)(或 \(x_{(u,v)},x_{(v,u)}\))\(,1\le i\le m\),变量个数 \(m=|E|>n(q-1)\)。再对每个点 \(u\in V\),构造域 \(\mathbb{F}_q\) 上的多项式 \(f_u\):
其中 \(N(u)\) 表示 \(v\) 的邻居集合。\([x_{(u,v)}\neq 0]\):当 \(x_{(u,v)}\) 不等于 \(0\) 时它返回 \(1\),其他情况返回 \(0\)。当各个变量的值确定后,可以根据 \(x_{(u,v)}\) 的值选择 \(G\) 的一个子图:若 \(x_{(u,v)}\neq 0\) ,则选择 \((u,v)\) 加入图 \(H\),否则不加入;\(H\) 的点集由这些边的端点组成。那么最终 \(H\) 中点 \(u\) 的邻居个数模 \(q\) 等于 \(f_u\) 的值。若 \(f_u=0\) 对所有 \(u\in V\) 成立,那么 \(d(u)\bmod q=0,0<d(u)\le 2q-1\),可以直接推出 \(H\) 是一个 \(q-regular\) 子图(当所有 \(x_i\) 都为 \(0\) 时,\(H\) 为空图,这是例外情况)。所以问题化为证明:
因为 \(\sum_{u\in V}\deg f_u=n(q-1)<m\),所以由 Theorem 3.2 可得:
易知 \(x_i=0,\forall 1\le i\le m\) 是 \(f_u(u\in V)\) 的一组公共零点,所以 \(|Z|>0\),\(|Z|\ge p\),\(Z\) 中应至少含有一组非零解,\((3.3.1)\) 式得证。Q.E.D.
Lemma 3.4. 任何图 \(G=(V,E)\),一定包含一个二分图子图 \(H\),其中一边的点集为 \(V_1\),另一边的点集为 \(V_2\),满足:\(H\) 是 \(\delta-half-regular\) 的,\(\delta\ge d(G)/4\)(一个二分图被称为是 \(\delta-half-regular\) 的,当且仅当 \(d(v)=\delta,\forall v\in V_1\) 且 \(|V_1|\ge|V_2|\))。
若随机将 \(V\) 分成两个子集,只保留它们之间的连边,去掉子集内部的边,这样生成的二分图边数的期望为原图边数的 \(1/2\)(每条边有 \(1/2\) 概率被保留)。所以一定存在一个二分图子图 \(G'=(V',E')\),满足 \(|E'|\ge |E|/2\),\(d(G')\ge d(G)/2\)。
接下来对 \(G'\) 不停地做这样的操作:任取 \(V'\) 中度数最小的点 \(v\),若 \(d(v)<d(G')/2\),就删去点 \(v\) 及它连出去的边,删去后边数变为 \(|E'|-d(v)=|V'|d(G')/2-d(v)>(|V'|-1)d(G')/2\),所以平均度数一定递增,直到 \(d(v)\ge d(G')/2\) 操作停止。此时设得到的新图为 \(G''=(V'',E'')\),那么 \(d(v)\ge d(G'')/2\ge d(G')/2\ge d(G)/4,\forall v\in V''\),即最小度数的点的度数 \(\ge d(G)/4\)。
此时的图 \(G''\) 仍是二分图,设一边的点集为 \(V_1''\),另一边的点集为 \(V_2''\)。不妨设 \(|V_1''|\ge |V_2''|\),对所有 \(v\in V_1''\),\(d(v)\ge d(G)/4\),可以通过删边使得 \(V_1''\) 一侧所有点的度数都为 \(\delta\),且 \(\ge d(G)/4\)。这样得到的新图 \(H\) 就是 \(\delta-half-regular\) 的。Q.E.D.
Lemma 3.5. 二分图 \(G\) 是 \(\delta-half-regular\) 的:一边的点集为 \(X\),另一边的点集为 \(Y\),满足 \(|X|\ge |Y|\) 且 \(|X|\) 中所有点度数为 \(\delta\)。若 \(G\) 的任何子图都不是 \(\delta-half-regular\) 的,那么 \(|X|=|Y|\),且存在一组完美匹配。
若 \(|X|>|Y|\),则可以从 \(|X|\) 中删去一个点得到一个 \(\delta-half-regular\) 子图,矛盾。所以 \(|X|=|Y|\)。
对于 \(X\) 的任意子集 \(X'\),一定满足 \(|N(X')|\ge |X'|\)(否则 \(X'\cup N(X')\) 就诱导出了更小的 \(\delta-half-regular\) 子图)。由 Hall 定理 可得,\(G\) 一定存在一组完美匹配。
The Proof of Theorem 3 (Pyber Theorem) 对任意正整数 \(k\),存在一个常量 \(c_k\),满足:对于充分大的图 \(G=(V,E)\),\(|V|=n,|E|\ge c_kn\log n\),一定存在一个 \(k-regular\) 子图。
一定存在 \(q=p^i(i\in \mathbb{N})\),满足 \(k\le q\le 2k\)(\(q\) 是二的幂次时显然)。如果 \(G\) 中存在一个 \(q-regular\) 子图,且它还是二分图,那么由 Hall 定理 容易证明存在完美匹配,将完美匹配的边删去后就得到了 \((q-1)-regular\) 子图。重复进行这样的操作就可以得到 \(k-regular\) 子图。
下面证明:当 \(|E|\ge c_q n\log n\) 时,\(G\) 中存在一个 \(q-regular\) 二分图子图。
\(d(G)\ge c_q\log n\),由 Lemma 3.4 可知,\(G\) 中存在 \(\delta-half-regular\) 子图,\(\delta\ge c_q\log n/4\),我们选出其中一个极小的子图 \(G_0=(V_0,E_0)\),由 Lemma 3.5 可知,\(G_0\) 存在完美匹配,将完美匹配中的边删去之后将得到一个 \((\delta-1)-half-regular\) 子图,再选出其中一个极小的 \((\delta-1)-half-regular\) 子图 \(G_1=(V_1,E_1)\) …… 通过一系列这样的操作得到了一个子图序列:
序列中对任意 \(i<\delta-1\),\(G_{i+1}\) 是 \(G_i\) 的子图,\(G_i\) 是 \((\delta-i)-half-regular\) 的,且存在一个完美匹配,设它的完美匹配为 \(A_i\),那么 \(A_i\) 的边数为 \(|V_i|/2\)。考虑以下序列:
由于 \(G_{\delta-1}\) 非空,\(|V_{s(2q-2)}|>|V_{\delta-1}|\ge 1\),
而一定存在充分大的(与 \(n\) 无关的) \(c_q\),满足 \(\left(\frac{2q-2}{2q-3}\right)^s\ge \left(\frac{2q-2}{2q-3}\right)^{c_q\log n}>n\),所以一定存在 \(0\le x\le s-1\),满足
设 \(l=x(2q-2),r=(x+1)(2q-2)\),令图 \(H=(V_H,E_H)=A_{l}\cup A_{l+1}\cup \cdots\cup A_{r}\),则
所以 \(d(H)=2|E_H|/|V_H|>2q-2\)。
又因为 \(H\) 是 \(r-l+1\) 个不相交完美匹配的并,所以 \(\Delta(H)= 2q-1\)。由 Lemma 3.3 可知,\(H\) 中一定存在 \(q-regular\) 子图。又因为 \(H\) 包含于二分图 \(G_0\),所以 \(H\) 是 \(q-regular\) 的二分图。再由前面的证明可知,一定存在一个 \(k-regular\) 子图。Q.E.D.
Huang Hao Theorem (Induced subgraphs of hypercubes and a proof of the Sensitivity Conjecture)
Theorem 4. (Huang Hao Theorem) 令 \(Q_n\) 为 \(n\) 维超立方体图,它的顶点集由 \(\{0,1\}^n\) 中的向量组成,两个向量有边当且仅当它们恰在一个坐标上不同。对任意的 \(n\),对 \(Q_n\) 的任意一个诱导子图 \(H=(V,E)\),若 \(|V|=2^{n-1}+1\),则 \(\Delta(H)\ge \lceil\sqrt{n}\rceil\),并且这个界是紧的。
一个 \(\Delta(H)=\lceil \sqrt{n}\rceil\) 的构造:……
……
打字太累了,eden 放弃了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号