梯度消失与梯度爆炸问题

梯度消失、爆炸带来的影响

　　举个例子，对于一个含有三层隐藏层的简单神经网络来说，当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

　　　　　　

产生的原因

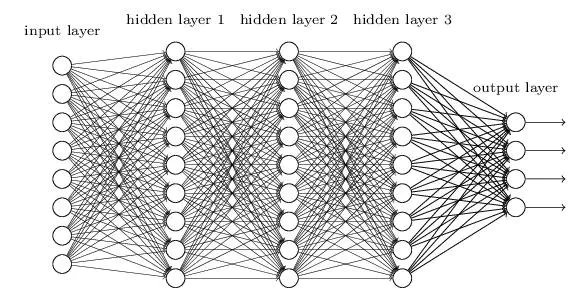
　　以上图中含有三个隐藏层的单神经元神经网络为例，激活函数使用 Sigmoid ：　　

　　　　$\sigma(x)=\frac{1}{1+e^{-x}}$

　　　　$\sigma^{\prime}(x)=\sigma(x)(1-\sigma(x))=-\left(\sigma(x)-\frac{1}{2}\right)^{2}+\frac{1}{4}$

　　图中是一个四层的全连接网络，假设每一层网络激活后的输出为 $f_i({x})$，其中 $i$ 为第 $i$ 层，$x$ 代表第 $i$ 层的输入，也就是第 $i−1$ 层的输出，$f$ 是激活函数，那么得出

　　　　$f_{i+1}=\sigma \left(f_{i} * w_{i+1}+b_{i+1}\right)$ 

　　记为 

　　　　$f_{i+1}=\sigma\left(f_{i} * w_{i+1}\right) $ 。 　　

　　BP算法基于梯度下降策略，以目标的负梯度方向对参数进行调整，参数的更新为 $w \leftarrow w+\Delta w$ ，如果要更新第二隐藏层的权值信息，根据链式求导法则，更新梯度信息： 

　　　　${\large \Delta w_{2}=\frac{\partial L o s s}{\partial w_{2}}=\frac{\partial L o s s}{\partial f_{4}} \frac{\partial f_{4}}{\partial f_{3}} \frac{\partial f_{3}}{\partial f_{2}} \frac{\partial f_{2}}{\partial w_{2}}} $

　　由 

　　　　$f_{2}=f\left(f_{1} * w_{2}\right)$

　　得

　　　　${\large \frac{\partial f_{2}}{\partial w_{2}}=\frac{\partial \sigma }{\partial\left(f_{1} * w_{2}\right)} \frac{\partial (f_{1} * w_{2} )}{\partial\left( w_{2}\right)}=\frac{\partial \sigma }{\partial\left(f_{1} * w_{2}\right)} *f_{1} =\sigma ^{\prime}*f_{1}} $

　　其中  $f_{1 }$是第一层的输出。

　　且

　　　　$\frac{\partial f_{4}}{\partial f_{3}}=\sigma ^{\prime} * w_{4}$

　　　　$\frac{\partial f_{3}}{\partial f_{2}}=\sigma^{\prime} * w_{3}$

　　对激活函数进行求导  $\sigma ^{\prime}$，如果此部分大于 1 , 那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸。如果此部分小于1，那么随着层数增多，求出的梯度更新信息将会以指数形式衰减， 即发生了梯度消失。另外，需要注意的是 $w$ 往往是矩阵形式，对于每个分量 $w_{ij}$ 分析如同激活函数。

　　　　$\Delta w_{2}=\frac{\partial L o s s}{\partial w_{2}}=\frac{\partial L o s s}{\partial f_{4}}\sigma ^{\prime} * w_{4}*\sigma ^{\prime} * w_{3}*\sigma ^{\prime}*f_{1}$

　　从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，属于先天不足。