线性回归的从零开始实现

线性回归的从零开始实现

　　在了解了线性回归的背景知识之后，现在我们可以动手实现它了。尽管强大的深度学习框架可以减少大量重复性工作，但若过于依赖它提供的便利，会导致我们很难深入理解深度学习是如何工作的。
　　首先，导入本节中实验所需的包或模块，其中的 matplotlib 包可用于作图，且设置成嵌入显示。

import torch 
from IPython import display 
from matplotlib import pyplot as plt #matplotlib包可用于作图，用来显示生成的数据的二维图。
import numpy as np 
import random

1 生成数据集

　　我们构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为 1000, 输入个数（特征数）为 2 。 给定随机生成的批量样本特征 $ \boldsymbol{X} \in \mathbb{R}^{1000 \times 2} $ ，我们使用线性回归模型真实权重 $ \boldsymbol{w}=[2,-3.4] $ 和偏差 $ b=4.2$ , 以及一个随机噪声项 $\epsilon $ 来生成标签
　　　　$\boldsymbol{y}=\boldsymbol{X} \boldsymbol{w}+b+\epsilon$
　　其中噪声项 $\epsilon$ 服从均值为 0、标准差为 0.01 的正态分布。噪声代表了数据集中无意义的干扰。下面，让我们生成数据集。

feature_size = 2
example_count = 1000
true_w = [2, -3.4]
true_b = 4.2

#生成特征，生成均值为0，方差为1 的特征矩阵
features = torch.tensor(np.random.normal(0, 1, (example_count, feature_size)), dtype=torch.float)

#输出特征矩阵的维度
print("特征矩阵的维度=",list(features.shape))

#根据线性方程得出特征对应的labels
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
#print(labels)

# 添加随机噪声
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
#print(labels)

　　注意，features 的每一行是一个长度为 2 的向量，而 labels 的每一行是一个长度为1的向量（标量）。
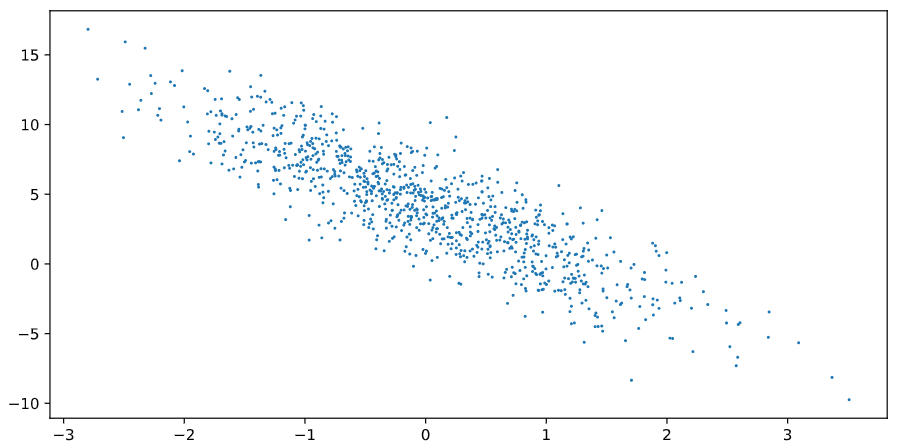
　　通过生成第二个特征features[:, 1]和标签 labels 的散点图，可以更直观地观察两者间的线性关系。

def use_svg_display(): 
    # 用矢量图显示 
    display.set_matplotlib_formats('svg') 
    
def set_figsize(figsize=(10, 5)): 
    use_svg_display() 
    # 设置图的尺寸 
    plt.rcParams['figure.figsize'] = figsize 
    
#绘制散点图
set_figsize() 
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1);

　　

2 读取数据

　　在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数：它每次返回 batch_size（批量大小）个随机样本的特征和标签。

def data_iter(batch_size, features, labels): 
    num_examples = len(features) 
    indices = list(range(num_examples)) 
    # 样本的读取顺序是随机的 
    random.shuffle(indices)  
    for i in range(0, num_examples, batch_size): 
        # 最后一次可能不足一个batch 
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) 
        yield  features.index_select(0, j), labels.index_select(0, j)

　　让我们读取第一个小批量数据样本并打印。每个批量的特征形状为(10, 2)，分别对应批量大小和输入个数；标签形状为批量大小

batch_sizes = 10

for xx, yy in data_iter(batch_sizes, features, labels):
    print(xx)
    print(yy)
    break

　　输出

　　

3 初始化模型参数

　　我们将权重初始化成均值为 0 、标准差为 0.01 的正态随机数，偏差则初始化成 0。

w = torch.tensor(np.random.normal(0, 0.01, (feature_size, 1)), dtype=torch.float32) 
b = torch.zeros(1, dtype=torch.float32)

　　之后的模型训练中，需要对这些参数求梯度来迭代参数的值，因此我们需要创建它们的梯度。

w.requires_grad_(requires_grad=True) 
b.requires_grad_(requires_grad=True)

4 定义模型

　　下面是线性回归的矢量计算表达式的实现。我们定义一元线性回归模型为 $\hat{y} =  w_1 x_1 +  w_2 x_2+b$

def linreg(X, w, b): 
    return torch.mm(X, w) + b

5 定义损失函数

　　定义损失函数为 $J=\frac{1}{2} \sum \limits _{i=1}^{N}\left(\hat{y}^{(i)}-f\left(x^{(i)}\right)\right)^{2}$
　　本实验使用平方损失来定义线性回归的损失函数。在实现中，我们需要把真实值 $𝑦$ 变形成 预测值 $\hat{y}$ 形状。以下的函数返回的结果和 $\hat{y}$ 的形状相同。

def squared_loss(y_hat, y):  
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

6 定义优化算法

　　以下的sgd函数实现了小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量大小来得到平均值。

def sgd(params, lr, batch_size): 
    for param in params: 
        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

7 训练模型

　　在训练中，我们将多次迭代模型参数。在每次迭代中，我们根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数 backward 计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量大小 batch_size 为10，每个小批量的损失l的形状为 (10, 1) 。由于变量l并不是一个标量，运行 l.backward() 将对l中元素求和得到新的变量，再求该变量有关模型参数的梯度。
　　在一个迭代周期（epoch）中，我们将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。我们会在后面“优化算法”一章中详细介绍学习率对模型的影响。

lr = 0.03 
num_epochs = 3 
batch_size = 10 
net = linreg 
loss = squared_loss 

for epoch in range(num_epochs):       # 训练模型一共需要num_epochs个迭代周期 
    
    # 在每一个迭代周期中，会使用训练数据集中所有样本一次 
    for X, y in data_iter(batch_size, features, labels):       # x和y分别是小批量样本的特征和标签 
        l = loss(net(X, w, b), y).sum()     # l是有关小批量X和y的损失 
        l.backward()     # 小批量的损失对模型参数求梯度 
        sgd([w, b], lr, batch_size)     # 使用小批量随机梯度下降迭代模型参数 
        w.grad.data.zero_()    # 梯度清零 
        b.grad.data.zero_() 
        
    train_l = loss(net(features, w, b), labels) 
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

　　输出：
　　　　epoch 1, loss 0.037224
　　　　epoch 2, loss 0.000135
　　　　epoch 3, loss 0.000052