平衡二叉搜索树(最小高度树)
二叉排序树
算法简介
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。该树属于一种输入数据就默认产生一种顺序的数据结构,这不像本章前面的内容所描述的静态的在某一个数据段内进行查找,动态查找是一种输入时就会自动对其进行排序的数据结构,前文学过的STL中的set集合其底层就是一个类似的树形结构红黑树。
定义
二叉排序树有以下性值:
a) 若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
b) 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
c) 左、右子树也分别为二叉排序树;
即对于每一个根结点,其左孩子永远小于根,右孩子永远大于根。
查找
考虑如果树是空的,则查找结束,无匹配。如果被查找的值和根结点的值相等,查找成功。否则就在子树中继续查找。如果被查找的值小于根结点的值就选择左子树,大于根结点的值就选择右子树。
BiTree SearchBST(BiTree T,KeyType key){
//如果递归过程中 T 为空,则查找结果,返回NULL;或者查找成功,返回指向该关键字的指针
if (!T || key==T->data) {
return T;
}else if(key<T->data){
//递归遍历其左孩子
return SearchBST(T->lchild, key);
}else{
//递归遍历其右孩子
return SearchBST(T->rchild, key);
}
}
插入
二叉排序的插入是建立在二叉排序的查找之上的,插入一个结点,就是通过查找发现该结点合适插入位置,把结点直接放进去。 其实在2.2节中一步步构造二叉排序树的过程中就是结点插入过程,并考虑查找的关键字已经有在树中,则指向该数据结点,若查找的关键字没有在树中,则指向查找路径上最后一个结点。
BOOL SearchBST(BiTree T,KeyType key,BiTree f,BiTree *p){
//如果 T 指针为空,说明查找失败,令 p 指针指向查找过程中最后一个叶子结点,并返回查找失败的信息
if (!T){
*p=f;
return false;
}
//如果相等,令 p 指针指向该关键字,并返回查找成功信息
else if(key==T->data){
*p=T;
return true;
}
//如果 key 值比 T 根结点的值小,则查找其左子树;反之,查找其右子树
else if(key<T->data){
return SearchBST(T->lchild,key,T,p);
}else{
return SearchBST(T->rchild,key,T,p);
}
}
//插入函数
BOOL InsertBST(BiTree T,ElemType e){
BiTree p=NULL;
//如果查找不成功,需做插入操作
if (!SearchBST(T, e,NULL,&p)) {
//初始化插入结点
BiTree s=(BiTree)malloc(sizeof(BiTree));
s->data=e;
s->lchild=s->rchild=NULL;
//如果 p 为NULL,说明该二叉排序树为空树,此时插入的结点为整棵树的根结点
if (!p) {
T=s;
}
//如果 p 不为 NULL,则 p 指向的为查找失败的最后一个叶子结点,只需要通过比较 p 和 e 的值确定 s 到底是 p 的左孩子还是右孩子
else if(e<p->data){
p->lchild=s;
}else{
p->rchild=s;
}
return true;
}
//如果查找成功,不需要做插入操作,插入失败
return false;
}
通过使用二叉排序树对动态查找表做查找和插入的操作,同时在中序遍历二叉排序树时,可以得到有关所有关键字的一个有序的序列。
例如,假设原二叉排序树为空树,在对动态查找表 {3,5,7,2,1} 做查找以及插入操作时,可以构建出一个含有表中所有关键字的二叉排序树,过程如图 2 所示:
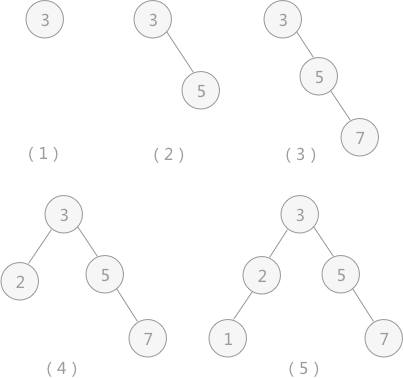
图 2 二叉排序树插入过程
通过不断的查找和插入操作,最终构建的二叉排序树如图 2(5) 所示。当使用中序遍历算法遍历二叉排序树时,得到的序列为:1 2 3 5 7 ,为有序序列。
删除
在查找过程中,如果在使用二叉排序树表示的动态查找表中删除某个数据元素时,需要在成功删除该结点的同时,依旧使这棵树为二叉排序树。
假设要删除的为结点 p,则对于二叉排序树来说,需要根据结点 p 所在不同的位置作不同的操作,有以下 3 种可能:
1、结点 p 为叶子结点,此时只需要删除该结点,并修改其双亲结点的指针即可;
2、结点 p 只有左子树或者只有右子树,如果 p 是其双亲节点的左孩子,则直接将 p 节点的左子树或右子树作为其双亲节点的左子树;反之也是如此,如果 p 是其双亲节点的右孩子,则直接将 p 节点的左子树或右子树作为其双亲节点的右子树;
3、结点 p 左右子树都有,此时有两种处理方式:
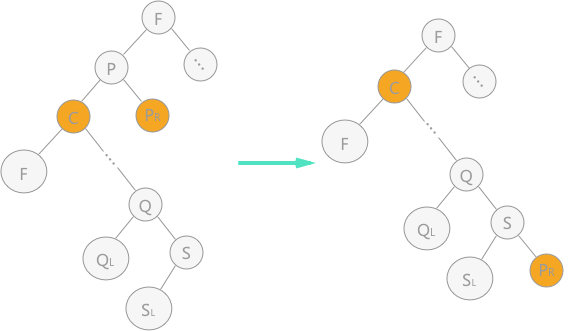
图 3 二叉排序树中删除结点(1)
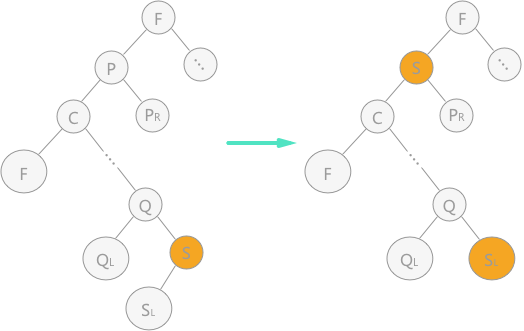
图 4 二叉排序树中删除结点(2)
图 4 中,在对左图进行中序遍历时,得到的结点 p 的直接前驱结点为结点 s,所以直接用结点 s 覆盖结点 p,由于结点 s 还有左孩子,根据第 2 条规则,直接将其变为双亲结点的右孩子。
//删除函数
int Delete(BiTree *p)
{
BiTree q, s;
//情况 1,结点 p 本身为叶子结点,直接删除即可
if (!(*p)->lchild && !(*p)->rchild) {
*p = NULL;
}
else if (!(*p)->lchild) { //左子树为空,只需用结点 p 的右子树根结点代替结点 p 即可;
q = *p;
*p = (*p)->rchild;
free(q);
}
else if (!(*p)->rchild) {//右子树为空,只需用结点 p 的左子树根结点代替结点 p 即可;
q = *p;
*p = (*p)->lchild;//这里不是指针 *p 指向左子树,而是将左子树存储的结点的地址赋值给指针变量 p
free(q);
}
else {//左右子树均不为空,采用第 2 种方式
q = *p;
s = (*p)->lchild;
//遍历,找到结点 p 的直接前驱
while (s->rchild)
{
q = s;
s = s->rchild;
}
//直接改变结点 p 的值
(*p)->data = s->data;
//判断结点 p 的左子树 s 是否有右子树,分为两种情况讨论
if (q != *p) {
q->rchild = s->lchild;//若有,则在删除直接前驱结点的同时,令前驱的左孩子结点改为 q 指向结点的孩子结点
}
else {
q->lchild = s->lchild;//否则,直接将左子树上移即可
}
free(s);
}
return TRUE;
}
int DeleteBST(BiTree *T, int key)
{
if (!(*T)) {//不存在关键字等于key的数据元素
return FALSE;
}
else
{
if (key == (*T)->data) {
Delete(T);
return TRUE;
}
else if (key < (*T)->data) {
//使用递归的方式
return DeleteBST(&(*T)->lchild, key);
}
else {
return DeleteBST(&(*T)->rchild, key);
}
}
}
完整代码

#include<iostream>
#include<stdlib.h>
using namespace std;
struct BiTNode{
int data;
BiTNode* lchild,*rchild;
};
typedef BiTNode * BiTree;
//二叉排序树查找算法
int SearchBST(BiTree T,int key,BiTree f,BiTree *p){
if (!T)
{
//如果 T 指针为空,说明查找失败,令 p 指针指向查找过程中最后一个叶子结点,并返回查找失败的信息
*p=f;
return false;
}
//如果相等,令 p 指针指向该关键字,并返回查找成功信息
else if (key==T->data)
{
*p=T;
return true;
}//如果 key 值比 T 根结点的值小,则查找其左子树;反之,查找其右子树
else if (key<T->data)
{
return SearchBST(T->lchild,key,T,p);
}else
{
return SearchBST(T->rchild,key,T,p);
}
}
int InsertBST(BiTree *T, int e) {
BiTree p=NULL;
if (!SearchBST((*T),e,NULL,&p))
{
//初始化插入结点
BiTree s =new BiTNode;
s->data=e;
s->lchild=s->rchild=NULL;
//如果 p 为NULL,说明该二叉排序树为空树,此时插入的结点为整棵树的根结点
if (!p)
{
*T=s;
}
else if (e<p->data)
{
p->lchild=s;
}else
{
p->rchild=s;
}
return true;
}
//如果查找成功,不需要做插入操作,插入失败
return false;
}
int Delete(BiTree *p){
BiTree q,s;
//情况 1,结点 p 本身为叶子结点,直接删除即可
if (!(*p)->lchild&&!(*p)->rchild)
{
*p=NULL;
}
else if (!(*p)->lchild)
{
q=*p;
*p=(*p)->rchild;
free(q);
}else if (!(*p)->rchild) {//右子树为空,只需用结点 p 的左子树根结点代替结点 p 即可;
q = *p;
*p = (*p)->lchild;//这里不是指针 *p 指向左子树,而是将左子树存储的结点的地址赋值给指针变量 p
free(q);
}else {//左右子树均不为空,采用第 2 种方式
q = *p;
s = (*p)->lchild;
//遍历,找到结点 p 的直接前驱
while (s->rchild)
{
q = s;
s = s->rchild;
}
//直接改变结点 p 的值
(*p)->data = s->data;
//判断结点 p 的左子树 s 是否有右子树,分为两种情况讨论
if (q != *p) {
q->rchild = s->lchild;//若有,则在删除直接前驱结点的同时,令前驱的左孩子结点改为 q 指向结点的孩子结点
}
else {
q->lchild = s->lchild;//否则,直接将左子树上移即可
}
free(s);
}
return true;
}
int DeleteBST(BiTree *T, int key)
{
if (!(*T)) {//不存在关键字等于key的数据元素
return false;
}
else
{
if (key == (*T)->data) {
Delete(T);
return true;
}
else if (key < (*T)->data) {
//使用递归的方式
return DeleteBST(&(*T)->lchild, key);
}
else {
return DeleteBST(&(*T)->rchild, key);
}
}
}
void order(BiTree t)//中序输出
{
if (t == NULL) {
return;
}
order(t->lchild);
cout<<t->data<<" ";
order(t->rchild);
}
int main()
{
int i;
int a[5] = { 3,4,2,5,9 };
BiTree T = NULL;
for (i = 0; i < 5; i++) {
InsertBST(&T, a[i]);
}
cout<<"中序遍历二叉排序树:"<<endl;
order(T);
cout<<endl;
cout<<"删除3后,中序遍历二叉排序树:";
DeleteBST(&T, 3);
order(T);
}
因上求缘,果上努力~~~~ 作者:别关注我了,私信我吧,转载请注明原文链接:https://www.cnblogs.com/BlairGrowing/p/12840110.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号