滑动窗口

题目描述

有一个长为 n 的序列 a，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1,3,−1,−3,5,3,6,7], and k = 3。

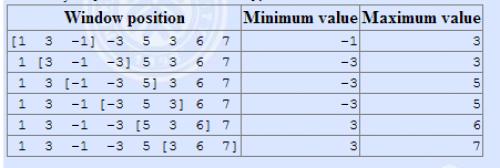
输入格式

输入一共有两行，第一行有两个正整数 n,k。 第二行 n 个整数，表示序列 a

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

输入输出样例

输入 #1

8 3
1 3 -1 -3 5 3 6 7

输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明/提示

【数据范围】
对于 50\%50% 的数据，1≤n≤105；
对于 100\%100% 的数据，1≤k≤n≤106，ai​∈[−231,231)。

分析：

就拿样例来谈谈，设以最小的为标准。

8 3
1 3 -1 -3 5 3 6 7

下文中我们用q来表示单调队列，p来表示其所对应的在原列表里的序号。

1. 由于此时队中没有一个元素，我们直接令1进队。此时，q={1},p={1}。

2. 现在3面临着抉择。下面基于这样一个思想:假如把3放进去，如果后面2个数都比它大，那么3在其有生之年就有可能成为最小的。此时，q={1,3},p={1,2}

3. 下面出现了-1。队尾元素3比-1大，那么意味着只要-1进队，那么3在其有生之年必定成为不了最小值，原因很明显:因为当下面3被框起来，那么-1也一定被框起来，所以3永远不能当最小值。所以，3从队尾出队。同理，1从队尾出队。最后-1进队，此时q={-1},p={3}

4. 出现-3，同上面分析，-1>-3，-1从队尾出队,-3从队尾进队。q={-3}，p={4}。

5. 出现5，因为5>-3，同第二条分析，5在有生之年还是有希望的，所以5进队。此时，q={-3,5},p={4,5}

6. 出现3。3先与队尾的5比较，3<5，按照第3条的分析，5从队尾出队。3再与-3比较，同第二条分析，3进队。此时，q={-3,3},p={4,6}

7. 出现6。6与3比较，因为3<6，所以3不必出队。由于3以前元素都＜3，所以不必再比较，6进队。因为-3此时已经在滑动窗口之外，所以-3从队首出队。此时，q={3,6},p={6,7}

8. 出现7。队尾元素6小于7，7进队。此时，q={3,6,7},p={6,7,8}。

 

#include<iostream>
using namespace std;

struct queues{
    static const int maxn=1000001;
    int n,k,a[maxn];
    int q[maxn],head,tail,p[maxn];
    //读入数据
    void read(){
        cin>>n>>k;
        for (int i = 1; i <=n; i++)
        {
            cin>>a[i];
        }
    }

    void findmax(){
        head=1;
        tail=0;
        for (int i = 1; i <=n; i++)
        {
            while (head<=tail&&q[tail]<=a[i])
                tail--;            
            q[++tail]=a[i];
            p[tail]=i;
            while (p[head]<=i-k)
                head++;
            if(i>=k)cout<<q[head]<<" ";            
        }
        cout<<endl;
    }


    void findmin(){
////为啥要这样呢?因为head要严格对应首元素，tail要严格对应尾元素，所以当tail>=head时，说明有元素。而一开始队列为空，说一要这样赋值。其实这跟普通队列一样。
        head = 1;
        tail=0;
        for (int i = 1; i <= n; i++)
        {
            //a[i]表示当前要处理的值
            //只要队列里有元素，队尾元素比待处理的值大，表示尾元素已经不可能出现
            while(head<=tail&&q[tail]>=a[i])tail--;
            q[++tail]=a[i];
            p[tail]=i;
            while (p[head]<=i-k)
                head++;//如果队首元素不在窗口内，表示其已经没用，出队
            if(i>=k)cout<<q[head]<<" ";                
        }
        cout<<endl;
    }
}worker;


int main(){
    worker.read();
    worker.findmin();
    worker.findmax();


}