洛谷OJ 3381 最小费用最大流（SPFA代码模版）

题目描述

如题，给出一个网络图，以及其源点和汇点，每条边已知其最大流量和单位流量费用，求出其网络最大流和在最大流情况下的最小费用。

输入输出格式

输入格式：

 

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含四个正整数ui、vi、wi、fi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi），单位流量的费用为fi。

 

输出格式：

 

一行，包含两个整数，依次为最大流量和在最大流量情况下的最小费用。

 

输入输出样例

输入样例#1：

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

输出样例#1：

50 280

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=1000，M<=1000

对于100%的数据：N<=5000，M<=50000

样例说明：

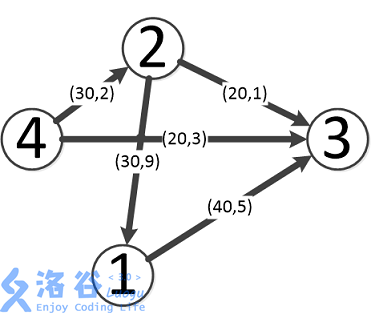
如图，最优方案如下：

第一条流为4-->3，流量为20，费用为3*20=60。

第二条流为4-->2-->3，流量为20，费用为（2+1）*20=60。

第三条流为4-->2-->1-->3，流量为10，费用为（2+9+5）*10=160。

故最大流量为50，在此状况下最小费用为60+60+160=280。

故输出50 280。

 

代码模版题，测试一下模版是否正确

代码：

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 10010;
const int M = 100010;
struct edge
{
    int to, nxt;
    int cap, cost;
};
edge E[M << 1];
int head[N], tot;
int d[N], mf, mc, path[N], pre[N];
int vis[N];

void init()
{
    CLR(head, -1);
    tot = 0;
    mc = mf = 0;
}
inline void add(int s, int t, int cap, int cost)
{
    E[tot].to = t;
    E[tot].cap = cap;
    E[tot].nxt = head[s];
    E[tot].cost = cost;
    head[s] = tot++;
    E[tot].to = s;
    E[tot].cap = 0;
    E[tot].nxt = head[t];
    E[tot].cost = -cost;
    head[t] = tot++;
}
int spfa(int s, int t)
{
    CLR(d, INF);
    CLR(vis, false);
    queue<int>Q;
    Q.push(s);
    d[s] = 0;
    path[s] = 0;
    pre[s] = -1;
    vis[s] = 1;
    int now, v, i;
    while (!Q.empty())
    {
        now = Q.front();
        Q.pop();
        vis[now] = false;
        for (i = head[now]; ~i; i = E[i].nxt)
        {
            v = E[i].to;
            if (d[v] > d[now] + E[i].cost && E[i].cap > 0)
            {
                d[v] = d[now] + E[i].cost;
                path[v] = i;
                pre[v] = now;
                if (!vis[v])
                {
                    vis[v] = true;
                    Q.push(v);
                }
            }
        }
    }
    return d[t] != INF;
}
void mfmc(int s, int t)
{
    while (spfa(s, t))
    {
        int f = INF;
        for (int i = t; i != s && ~i; i = pre[i])
            f = min<int>(f, E[path[i]].cap);
        for (int i = t; i != s && ~i; i = pre[i])
        {
            E[path[i]].cap -= f;
            E[path[i] ^ 1].cap += f;
        }
        mf += f;
        mc += f * d[t];
    }
}
int main(void)
{
    int n, m, s, t, a, b, c, i, d;
    while (~scanf("%d%d%d%d", &n, &m, &s, &t))
    {
        init();
        for (i = 0; i < m; ++i)
        {
            scanf("%d%d%d%d", &a, &b, &c, &d);
            add(a, b, c, d);
        }
        mfmc(s, t);
        printf("%d %d\n", mf, mc);
    }
    return 0;
}