树状数组

定义：

树状数组就是用树形结构模拟数组，维护前缀信息的数据结构。

用途：

> 单点更新，单点查询

> 单点更新，区间查询

> 区间更新，单点查询

> 区间更新，区间查询

当然对于第一个没有必要用树状数组。

引入：

丢个问题，给定序列长 $m$ 的数组，有 $p$ 组询问，当 $a=1$ 时求出 $b$ 到 $c$ 的和，当 $a=0$ 时将 $b$ 到 $c$ 区间的值加上 $d$ 

怎么办？暴力枚举修改？再枚举求和？不行，复杂度上了天，$TLE$ 非你莫属。

这里用树状数组解决问题？步入正题。

图示：

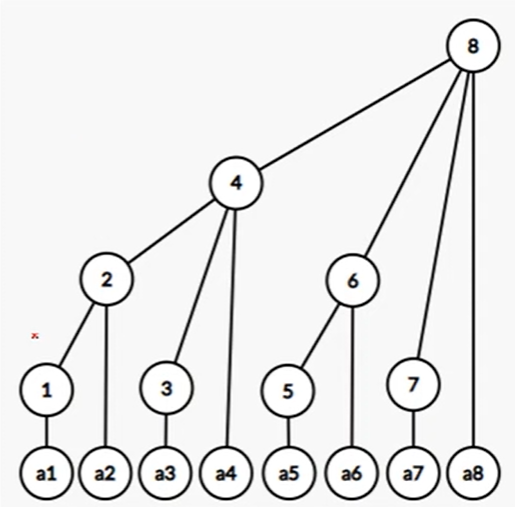
这就是一个树状数组，设原数组为 $a$ ，树状数组为 $c$。

结论：

我们观察上图，发现什么？

$c1$ 维护了 $a1$ 的和，$c2$ 维护了 $a1+a2$ 的和，$c3$ 维护了 $a3$ 的和，$a4$ 维护了 $a1+a2+a3+a4$ 的和，以此类推。

没发现什么？正常人第一眼都看不出来。

将树状数组变一下表示方式，用二进制数表示编号

$1\rightarrow1$，$2\rightarrow10$，$3\rightarrow11$，$4\rightarrow100$，$5\rightarrow101$，$6\rightarrow110$，$7\rightarrow111$，$8\rightarrow1000$

看出来了吗？还没？

注意二进制末尾零的个数，设个数为 $k$。

$1，3，7$后没有$0$ 、$2，6$后一个 $0$……以此类推，会发现这个数组维护 $a$ 数组的个数就是 $2^k$ 个。

所以该数组维护的值为：

$$c[i]=\sum_{j=1}^{2^k}a[i-{2^k}+j]$$

既然是一颗树状数组，如何找父节点和前一个兄弟节点？( 兄弟节点：如上图2,3为兄弟节点，4,6,7为兄弟节点)

我们再看，不难发现对于第 $i$ 个节点的父节点编号为 $i+2^k$，其前一个兄弟节点编号为 $i-2^k$ 。

有什么用？举个例子，如果要查询 $a[5]$ 的值，那你查 $c[5]$ 是没用问题的，因为 $c[5]$ 只维护了 $a[5]$ 一个元素。

那查 $a[4]$ 呢？可不能查$c[4]$，因为 $c[4]$ 维护的是 $\sum_{i=1}^{4}a[i]$的值，所以要查$a[4]$，则需要求$c[4]-c[3]-c[2]$，显然可以通过找兄弟节点求出了$c[3]$和$c[2]$ 的值。

lowbit：

求出下一个$2^k$。

int lowbit(int i){return i&(-i)};

简单一行，原理牵扯到计算机底层的计算，有关二进制的原码和补码，在计算中 $i$ 会被转化为二进制数，在计算机中一个正数的补码与原码相同，负数的补码等于原码的反码加一，

有点晦涩，举个例子：一个二进制数 $00001010$ 对应的负数的二进制就是"00000101"，进行按位与操作之后得到“10”，所以返回值就是 $2$，

不理解可以上图手摸一下，找到了$2^k$，那么就可以找到父节点和兄弟节点了。

操作：

$Fir$. 插入 

void Add(int x,int k){
	while(x<=n){
	   c[x]+=k;
	   x+=lowbit(x);	
	}
}

因为树状数组维护的是前缀信息，所以 $x$ 位置往后的 $c[i]$ 都加上了 $k$，如果不是区间修改的话，可以在 $x+1$ 的位置插入$-k$，那就实现了单点修改，给定范围的修改同理。

$Sec$. 查询

int get(int x){
	int res=0;
	while(x>0) res+=c[x],
	x-=lowbit(x); return res;
}

这就查询了 $x$ 的前缀信息，对于单点的操作可以维护一个差分数组。

例题：

P3374 【模板】树状数组 1

P3368 【模板】树状数组 2

P1908 逆序对

P2357 守墓人（什么阳间题目）

做题太少，有待补充。

后记：

大菜鸡一个，写错了 $d$ 我。