『具体数学』第1章 递归问题

  一切的开始。

典例选讲

hanoi塔

  问题较为经典：在一根柱子上从下往上按照大小顺序摞着 \(64\) 片圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。要求出需要移动多少次圆盘。
  想要解决问题，书中便借此问题引出一些解决问题的通法：

  (1)先研究小的情形
  (2)命名并求解

  经过这两步与一些基础的构造，不难把hanoi塔问题变为一组递归式：

\[\begin{array}{ll} &T_0 = 0;\\ &T_n \leq 2T_{n-1}+1, n>0. \end{array} \]

  接下来尝试得出这组递归式的解，即将递归式转换为等价的，且关于 \(T_n\) 的式子中不含 \(T\) 。我们将这种形式的式子称为封闭形式，这会使我们求解 \(T\) 所需的计算大大的减省。
  为了求解递推式，我们需要若干成体系的方法。数学归纳法便是众多方法中的一种，并且于这道题而言是一个非常不错的方法。
  数学归纳法并不是一个求解的方法，而是一个证明的方法。因此我们在使用数学归纳法之前需要有一个猜想，而 \(T\) 的值十分有规律，不难猜出 \(T_n = 2^n-1, n \geq 0\) 。
  在有了猜想之后，我们就可以开始使用数学归纳法进行证明。数学归纳法的步骤分为两步，首先是在 \(n\) 取最小值 \(n_0\) 时证明命题，这一步被称为基础（basis）。然后，对于所有 \(n>n_0\) ，假设 \(n_0\) 与 \(n-1\) 之间所有值已被证明，证明命题对 \(n\) 成立，这一步被称为归纳（induction）。这种方法可以让我们只使用两步就证明对于所有的 \(n\) 命题成立，不失为一种好的证明方法。
  hanoi塔的问题解决过程完美涵盖了解决一般问题的三个阶段：

  (1)研究小的情形。这有助于我们洞察问题，且对(2)(3)有所帮助。
  (2)对有意义的量求出数学表达式并给出证明数学表达式能完全涵盖原问题。一般而言我们能通过阶段获取有意义的递归式。
  (3)对数学表达式求出封闭形式并予以证明。

  当然解决hanoi塔递归式的方式不止是循规蹈矩的数学归纳法，一些灵光一闪也能帮助我们解递归式，例如令 \(U_i = T_i+1\) ，套进原递归式将会解得：

\[\begin{array}{ll} &U_0 = 1;\\ &U_n \leq 2U_{n-1}, n>0. \end{array} \]

  这种形态的递归式想必不需特别的技巧即可得知 \(U_i = 2^i\) ，这样解递归式十分有效，因此在解决问题时合理的想法是益处颇多的。

平面上的 \(V\)

  用 \(n\) 条直线最多能将一个平面分割成几个块，这个问题较为简单，不多讲，设这个数量为 \(L_n\) ，则递归式为 \(L_0 = 1, L_n = L_{n-1}+n\) ，通过等差数列求和公式可以得到递归式的解为 \(L_n = \frac{n(n+1)}2 + 1, n \geq 0\) 。
  接下来我们看一个相关问题：用 \(n\) 个 \(V\) 型最多能将一个平面分割成几个块。（ \(V\) 型是指在平面上同一个点出发的两条射线组成的图形）
  乍一看这个问题没什么头绪，但我们可以通过适当的转化，来讲问题变换为我们熟悉的递归式。将射线变成直线，我们得到了下面这张图：
  
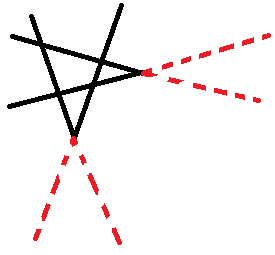
  这样就是 \(2n\) 条直线的答案，但是还要减去 \(2n\) ，因为 \(V\) 型相比于 \(2\) 条直线每个都少划分了 \(2\) 个区域，因此区域数 \(Z_n = L_{2n}-2n = 2n^2-n+1\) 。

约瑟夫问题

  另一个经典的问题：从围成标有记号 \(1\) 到 \(n\) 的圆圈的第 \(n\) 个人开始，每隔一个人删去一个人，直到只有一个人存活。

  然而 \(J(n)\) 看上去不如 \(T_n\) 一般有规律，能迅速找出递归式。这时我们可以分类讨论来帮助我们找出递归式：

  (1)对于 \(n\) 为偶数的情形，经过一轮后剩下的人号码都会翻倍并减一，即：

\[J(2n) = 2J(n)-1, n \geq 1 \]

  (2)对于 \(n\) 为奇数的情形，我们一并把编号 \(1\) 的人删掉，那么就相当于经过一轮后剩下的人号码都会翻倍并加一，即：

\[J(2n+1) = 2J(n)+1, n \geq 1 \]

  (3)组合上递归式的原始解 \(J(1) = 1\) ，总的递归式就长这样：

\[\begin{array}{lll} &J(1) = 1; &\\ &J(2n) = 2J(n)-1, &n\geq1;\\ &J(2n+1) = 2J(n)+1, &n\geq1. \end{array} \]

  这个递归式并不如前两个一样好解，尝试从表格中找规律：

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)	\(13\)	\(14\)	\(15\)	\(16\)
\(J(n)\)	\(1\)	\(1\)	\(3\)	\(1\)	\(3\)	\(5\)	\(7\)	\(1\)	\(3\)	\(5\)	\(7\)	\(9\)	\(11\)	\(13\)	\(15\)	\(1\)

  通过查表能够发现递归式的解为 \(J(2^m+l) = 2l+1, m \geq 0, 0 \leq l < 2^m\) ，然后使用数学归纳法即可证明。
  另外， \(J(n)\) 含有一个十分有趣的性质：先将 \(n\) 按二进制展开，即 \(n = (b_mb_{m-1}...b_1b_0)_2\) ，然后因为 \(J(n = 2m+l) = 2l+1\) 所以有 \(J((b_mb_{m-1}...b_1b_0)_2) = (b_{m-1}..b_1b_0b_n)\) ，即将 \(n\) 去掉了最高位的 \(1\) ，然后整体乘 \(2\) 再加上一个 \(1\) ，这样是等价于将 \(n\) 向左循环移动一位。不过因为要去掉前导零，所以除非 \(n = 2^x-1\) ，否则不能循环地转一圈。
  推广的，对于形如

\[\begin{array}{llll} &f(j) = \alpha_j, &1\leq j\leq d;\\ &f(dn+j) = cf(n)+\beta_j, &0\leq j\leq d,n\geq1. \end{array} \]

的递归式而言，它有变动基数的解：

\[f((b_mb_{m-1}...b_1b_0)_d)=(\alpha_{b_m}\beta_{b_{m-1}}\beta_{b_{m-2}}...\beta_{b_1}\beta_{b_0})_c \]

当然这个解的左半部分也可以把进制表示拆成和式表示：

\[f((b_mb_{m-1}...b_1b_0)_d)=\alpha_{b_m}c^m+\sum\limits_{0\leq i<m}\beta_{b_i}c^i \]

成套方法求解递归式

  前面我们解递归式的时候并没有一些成体系的方法，那么这里所介绍的便是用成套方法求解类约瑟夫问题的递归式。因为该方法与下一章中用成套方法解和式-递归式的一般形式有较多相通的部分，于是将两部分合并在一起。
  和式-递归式的一般形式犹如

\[\begin{array}{lll} &R_0 = \alpha;\\ &R_n = R_{n-1}+\beta+\gamma n, \quad n>0. \end{array} \]

那么该递归式的解可以写成这样的形式

\[R_n = A(n)\alpha+B(n)\beta+C(n)\gamma \]

其中 \(A(n)\) 、 \(B(n)\) 、 \(C(n)\) 是依赖于参数 \(\alpha\) 、 \(\beta\) 、 \(\gamma\) 的系数。
  而使用成套方法，就是用关于 \(n\) 简单函数来代替 \(R_n\) ，求出参数 \(\alpha\) 、 \(\beta\) 、 \(\gamma\) ，从而再求出系数。令 \(R_n = 1\) ，解得 \(\alpha = 1,\beta=0,\gamma = 0\) ，从而 \(A(n) = 1\) 。
  再令 \(R_n = n\) ，解得 \(\alpha = 0,\beta=1,\gamma = 0\) ，从而 \(B(n) = n\) 。
  再令 \(R_n = n^2\) ，解得 \(\alpha = 0,\beta=-1,\gamma = 2\) ，从而 \(2C(n)-B(n) = n^2\) ，解得 \(C(n) = \frac{n^2+n}2\) 。

  接下来解决类约瑟夫问题递归式。这里的例子用到的是习题(1.20)：

\[\begin{array}{llll} &h(1) = \alpha;\\ &h(2n+j) = 4h(n)+\gamma_jn+\beta_j, &j = 0, 1, &n \leq 1. \end{array} \]

  与前面的成套方法类似，我们设

\[R_n = A(n)\alpha+B(n)\gamma_0+C(n)\gamma_1+D(n)\beta_0+E(n)\beta_1 \]

然后尝试带入 \(h(n) = n\) 与 \(h(n) = n^2\) ，然后发现只有两个云里雾里的式子：

\[\begin{array}{llll} &A(n)+E(n)-2B(n)-2C(n)=n;\\ &A(n)+E(n)+4C(n)=n^2. \end{array} \]

  似乎无法找到有效的突破口，但是依靠在约瑟夫问题的最后得到的通解式子，我们可以通过其推出 \(A(n)\) 、 \(D(n)\) 、 \(E(n)\) 从而再代进上式求出 \(B(n)\) 、 \(C(n)\)：

\[\begin{array}{llll} &A(n) = 4^m;\\ &D(n) = \sum\limits_{i=0}^{m-1}4^i(1-b_i);\\ &E(n) = \sum\limits_{i=0}^{m-1}4^ib_i;\\ &C(n) = \frac{n^2}4-4^{m-1}-\sum\limits_{i=-1}^{m-2}4^ib_i\\ &B(n) = -\frac {n^2}4-3\times4^{m-1}-3\times\sum\limits_{i=-1}^{m-2}4^ib_i-\frac n2 \end{array} \]

即可完成此题。

方法小结

数学归纳法

  步骤：
  (1)基础（basis）：在 \(n\) 取最小值 \(n_0\) 时证明命题。
  (2)归纳（induction）：对于所有 \(n>n_0\) ，假设 \(n_0\) 与 \(n-1\) 之间所有值已被证明，证明命题对 \(n\) 成立。

  广义上，只要是能通过归纳法基础，用一些推广方式将证明范围内的 \(n\) 全部证明，都可以被称为归纳过程。下面的习题也将会有所涉及。

成套方法求解递归式

  步骤：
  (1)把封闭形式表示成 系数 \(\times\) 可能出现的数。
  (2)带入不同的简单函数，如 \(R_n = 1\) 、 \(R_n = n\) 、 \(R_n = 2^n\) 等，得到系数间的一些方程。
  (3)代入类约瑟夫递归式的通解，求出部分系数，再将这些系数代回(2)中得到的方程中解出剩余的系数。

习题选讲

  （由于书中难题的答案基本仅有思路与做法的启发，无法完全保证所写小部分题目答案的正确性）

1.9

  证明：

\[P(n): \prod\limits_{i=1}^nx_i\leq \left(\frac 1n\sum\limits_{i=1}^nx_i\right)^n, \quad x_1,\cdots,x_n\geq0. \]

  本题较为经典，在高中的练习中也有出现，对思维具有一定的启发性。

  我们考虑使用归纳法证明此题，首先有归纳法基础 \(P(2)\) 成立，证明就是均值不等式，略。

  但是能够发现，并没有办法可以从 \(2\sim n\) 推广到 \(n+1\) ，但是有另外两种推广：

  (1)令 \(x_n = \frac 1{n-1}\sum^{n-1}_{i=1}x_i\) ，有：

\[\begin{array}{lll} & &\prod\limits_{i=1}^nx_i\leq \left(\frac 1n\sum\limits_{i=1}^nx_i\right)^n\\ &\Leftrightarrow &\prod\limits_{i=1}^nx_i\leq \left(\frac 1{n-1}\sum\limits_{i=1}^{n-1}x_i\right)^{n-1}x_n\\ &\Leftrightarrow &\prod\limits_{i=1}^{n-1}x_i\leq \left(\frac 1{n-1}\sum\limits_{i=1}^{n-1}x_i\right)^{n-1} \end{array} \]

即 \(P(n)\) 蕴含 \(P(n-1)\) 。

  (2)

\[\begin{array}{lll} & &\prod\limits_{i=1}^nx_i\leq \left(\frac 1n\sum\limits_{i=1}^nx_i\right)^n\\ &\Leftrightarrow &\prod\limits_{i=1}^{2n}x_i\leq \left(\frac 1n\sum\limits_{i=1}^nx_i\frac 1n\sum\limits_{i=n+1}^{2n}x_i\right)^n\\ &\Leftrightarrow &\prod\limits_{i=1}^{2n}x_i\leq \left(\frac 1{2n}\sum\limits_{i=1}^{2n}x_i\right)^{2n}(from \quad P(2))\\ \end{array} \]

即 \(P(n)\) 蕴含 \(P(2n)\) 。

  可以发现(2)虽然可以无限推广，但推广过程中存在许多间隙，而这正好可以使用(1)的稠密性补充证明，因此该命题对于任意 \(\geq 1\) 的数均为真。这就是反向归纳法，用一种与会的方式通过无限推广后回推证明命题，使用的关键往往是找到如(1)一般能补全无限推广缺口的推广形式，如本题中 \(n\) 蕴含 \(n-1\)。

1.14

  问题:记在一个三维空间上使用 \(n\) 个平面分割出的最多空间数为 \(P_n\) ，求 \(P_n\) 的递归式。

  仅处理这道题的话并不是十分困难，考虑新加入的平面能够产生的区域数为先前的平面与该平面交边所构成的二维平面区域数，所以有 \(P_n = P_{n-1}+L_{n-1}\) 。

  我们发现这个问题极易推广到高维的情形，于是另 \(P_n^k\) 表示对于 \(k\) 维空间，用 \(k-1\) 维超平面分割 \(n\) 次所能得到的最大划分数，由前面的推断可以得到递归式： \(P_n^k = P_{n-1}^k+P_{n-1}^{k-1}\) 。

  进一步地，通过习题答案中所给出 \(k=1,k=2,k=3\) 时的封闭形式对我们的启发，猜测该递归式有封闭形式： \(P_n^k = \sum\limits_{i=0}^n\binom{n}{i}\) ，并对其使用归纳法证明：

  首先，该递归式有归纳法的基础 \(P_n^1 = 1+n = \binom{n}{0}+\binom{n}{1}\) ，由此可以开始归纳：

\[\begin{array}{rll} P_n^k-P_{n-1}^k &= &P_{n-1}^{k-1}\\ P_{n-1}^k-P_{n-2}^k &= &P_{n-2}^{k-1}\\ &\cdots\\ P_1^k-P_0^k &= &P_0^{k-1}\\ \end{array} \]

将上式相加得到：

\[\begin{array}{rll} P_n^k-1 &= &\sum\limits_{i=0}^{n-1}P_i^{k-1}\\ P_n^k &= &1+\sum\limits_{i=0}^{n-1}P_i^{k-1}\\ &= &1+\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{k-1}\binom{i}{j}\\ &= &1+\sum\limits_{j=0}^{k-1}\sum\limits_{i=j}^{n-1}\binom{i}{j}\\ &= &1+\sum\limits_{j=0}^{k-1}\binom{n}{j+1} \quad(\text{此处用到基本恒等式中的上指标求和法})\\ &= &1+\sum\limits_{j=0}^{k-1}\binom{n}{j+1}\\ &= &1+\sum\limits_{j=1}^{k}\binom{n}{j}\\ &= &\sum\limits_{j=0}^{k}\binom{n}{j}\\ \end{array} \]

证毕。

1.20

  上文已提到，故在此略过。

1.23

  约瑟夫游戏，要求幸存者编号为 \(j\) ，可以任意选择淘汰参数 \(q\) 使得每隔 \(q-1\) 个人处死一个，求是否总能满足要求。

  朴素地，对于 \(n\leq2\) ，一定有解。下面讨论 \(n>2\) 的情况。

  首先设 \(L = \text{lcm}(1,2,\cdots,n)\) ，能够发现只需讨论 \(j > n/2\) 的情况即可，因为参数为 \(q' = L+1-q\) 时留下 \(j' = n+1-j\) 当且仅当参数为 \(q\) 时留下 \(j\) 。

  由于 \(n > 2\) ，根据Bertrand假设，有 \(\exists p\in(\frac{n}{2}, n] \cup \{ prime \}\) ，此时可得到 \(\gcd(p,L/p) = 1\) 。考虑构造处决编号序列为： \(1,2,\cdots,n-p,j+1,j+2,\cdots,n,n-p+1,\cdots,j-1\) ，此时参数 \(q\) 满足条件：

\[\left\{ \begin{array}{ll} q\equiv1\pmod {L/p}\\ q\equiv j+1-n\pmod p \end{array} \right. \]

  由中国剩余定理可得这样的 \(q\) 一定存在，因此总能满足要求。