ARC176 题解

AtCoder Regular Contest 176

A - 01 Matrix Again

考虑令 \(S_z = \{(x, y) | x + y = z\}\)，显然有一下几个性质：

• \(|S_z| = n\)；
• \(S_z\) 对 \(n\) 行 \(n\) 列的贡献均为 \(1\)；
• 每个点属于一个集合。

所以即选择 \(m\) 个集合种的点即可，复杂度 \(\mathcal O(nm)\)。

提交记录：https://atcoder.jp/contests/arc176/submissions/52817630。

B - Simple Math 4

简单推到后不难发现答案为 \(2^{(n - k) \bmod (m - k) + k}\)，注意特判整除和 \(n < k\) 等特殊情况。

提交记录：https://atcoder.jp/contests/arc176/submissions/52819968。

C - Max Permutation

转化题意后即：

• 每个点 \(i\)，均有一个限制 \(p_i \le z_i\)；
• 有 \(m\) 条限制要求 \(p_{a_i} = c_i \lor p_{b_i} = c_i\)。

考虑在值域上从大到小遍历，遍历到 \(x\) 时，将 \(z_i = x\) 的 \(i\) 加入备选集合，特殊处理有限制的 \(x\)，由于限制涉及到的点一定满足 \(z_i = x\) 所以不需要考虑其对备选集合有特殊影响。

提交记录：https://atcoder.jp/contests/arc176/submissions/52819727。

D - Swap Permutation

考虑经典拆贡献，枚举 \(x\)，令 \(P^\prime_i = [P_i \le x]\)。那么该 \(x\) 的贡献即序列种 \(0, 1\) 对的数量。在进一步拆到 \((i, i + 1)\) 的贡献，考虑可以 DP，令 \(f_{0/1/2}\) 表示 \((P_i, P_{i + 1})\) 分别是 \((0, 0)\) 或 \((1, 1)\) 或 \((0, 1)/(1, 0)\) 的方案数，可以通过矩阵优化。

注意到转移只更当前有几个 \(0, 1\) 有关，所以对于一个 \(x\) 转移矩阵均相同，所以只需要维护三种初始状态的数量即可省区 \(i\) 的枚举。

时间复杂度 \(\mathcal O(nk^3\log m)\)。

提交记录：https://atcoder.jp/contests/arc176/submissions/52826417。

E - Max Vector

考虑最小割建模，由于值域极小，所以对于每一个 \(X_i, Y_i\) 都拆点成 \(x_{i, 0 \sim V}\) 和 \(y_{i, 0 \sim V}\)。令 \(x_{i, V + 1} = S\)，连接边：

• \((x_{i, j}, x_{i, j + 1}, j), (x_{i, j + 1}, x_{i, j}, \infty)\)，对应每一种取值；

• \((x_{i, X_i}, T)\)，表示 \(X^\prime_i \ge X_i\)；

• 对于每个操作建立虚点 \(q_k\)，连接 \((x_{i, a_{k, i}}, q_k, \infty), (q_k, y_{i, a_{k, i}}, \infty)\)，表示要么取 \(X\) 要么取 \(Y\)。

前两种边对于 \(y\) 取反建立，\(S\) 变为 \(T\)。

提交记录：https://atcoder.jp/contests/arc176/submissions/52831224。

F - Colorful Star

考虑 \(n \le 2 \lor m \le 1\) 时答案是不言自明的，先行特判，以下认为 \(n \ge 3, m \ge 2\)。

正难则反，考虑逆序操作，即那些树的终止形态能返回初始状态。一个覆盖操作的逆即：选定一条端点颜色相同的边，并将其中一个端点覆盖为任意颜色（以下操作均指逆操作）。

定义一个边的深度为：距离 \(0\) 较远的点到 \(0\) 的距离，称深度为 \(i\) 的边组成的集合为第 \(i\) 层。

由以上对逆操作的定义不难发现，端点颜色相同的边至关重要，我们称这种边为快乐边，按照快乐边数对终止状态分类有：

• 没有快乐边：一定无解；

• 有一条或两条快乐边（先通过若干次操作将快乐边移至第一层）：

  • \(1, \dots, n\) 号节点的不同颜色数小于 \(n - 1\) 或不同颜色数等于 \(n - 1\) 且 \(\exists 1 \le i \le n, n + 1 \le j \le 2n, c_i = c_j\)（即存在一对第一层和第二层的点颜色相同）：一定有解；
  • 反之：一定无解；

• 有三条以上的快乐边：一定有解；

第一类是 trivial 的，第三类等价于第二类（一定能用若干次操作使其变成第二类），所以重点研究第二类：

• 有解条件必要性：考虑不符合条件的情况即颜色均不相同或第一层共 \(n - 1\) 种颜色、第二层均为最后一种颜色，不难发现这种情况下，无论如何操作都无法使快乐边数增加，于是一定无解；
• 有解条件充分性：考虑若不同颜色数小于 \(n - 1\)，一定能牺牲掉一个重复的颜色使当前情况变成第二种情况，所以只用证明“有 \(n - 1\) 种颜色且存在一对第一层和第二层的点颜色相同”的情况。

考虑用构造证明：首先通过第一层和第二层的同色对一定能形成一条长度为 \(4\) 的链，我称它为快乐链，具体操作如图：

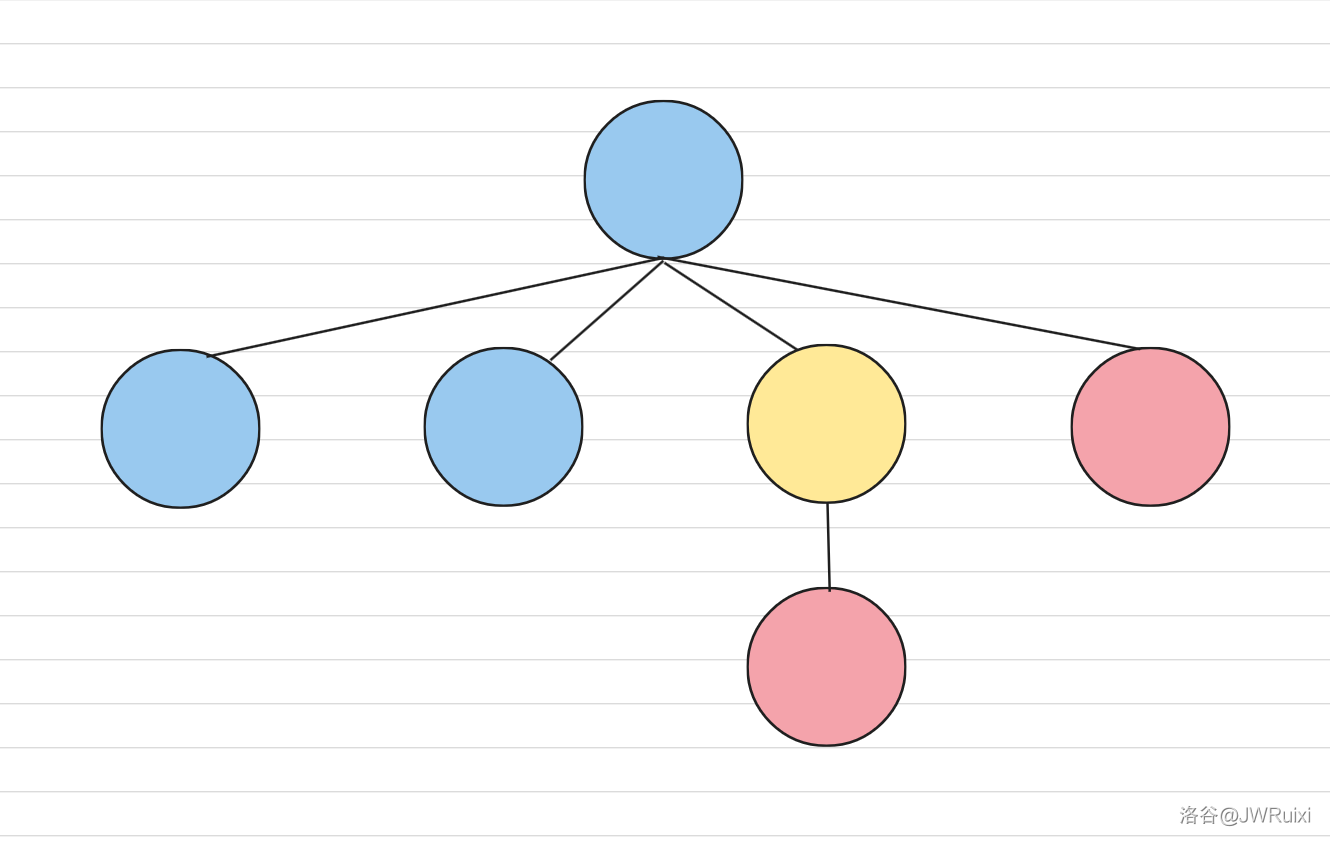
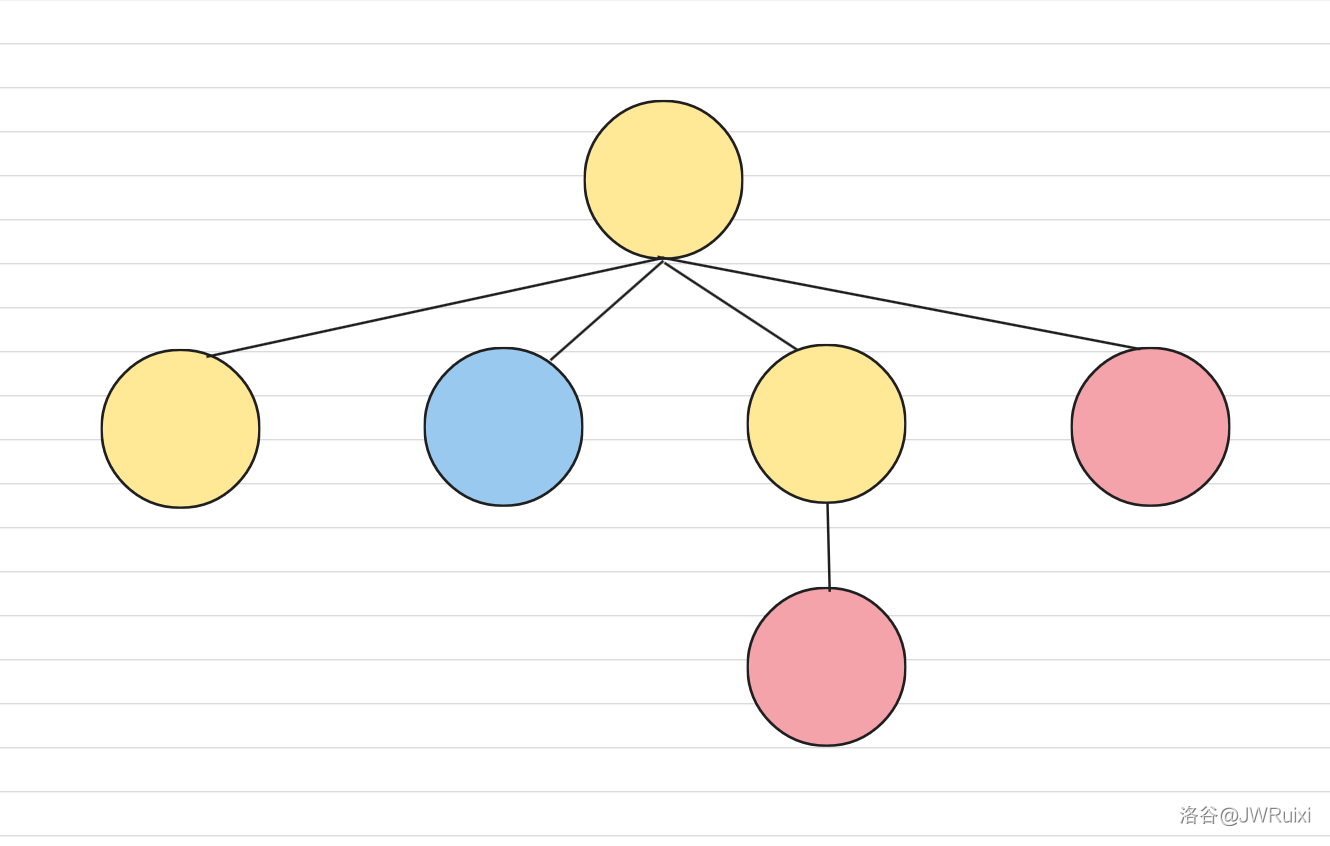
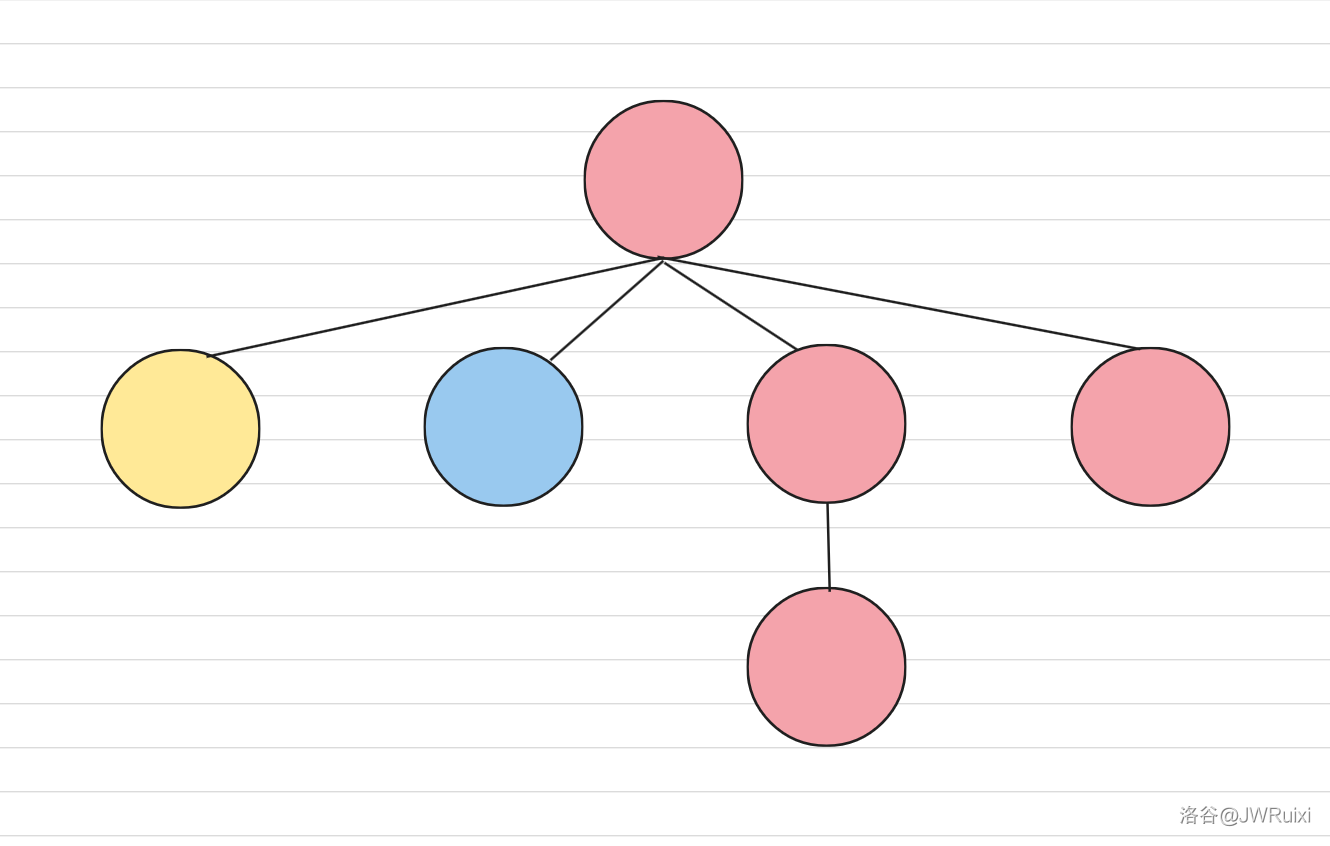
考虑我们的目标实际上等价于：同一条链上的点颜色相同，交换两条链的操作是简单的，具体的可以先考虑正向操作在推反向操作。

设这个同色对为 \((u, v)\) 其中 \(u\) 为第一层，\(v\) 为第二层。考虑选择一个第二层的节点 \(z\)，满足 \(c_z\) 在第二层出现的次数最多。将快乐链移动使得 \(z\) 在它上面，考虑 \(z\) 子树内最深的不是该链目标颜色的点，那么可以通过将第二层的那条边向下移动将它改为目标颜色。将快乐链的剩余三个点放回前两层后，由于我们选择的 \(z\) 点的颜色数是极大的，所以一定还能满足判断有解的两个条件之一。不断重复该过程即可解决 \(3 \sim m\) 层。第一、二层是 trivial 的。至此我们证明了充分性。

统计答案我们考虑容斥掉不合法的部分，即第一层颜色互不相同，或第一层有 \(n - 1\) 种颜色且第二层是剩下的一种颜色。

时间复杂度 \(\mathcal O(n)\)。

提交记录：https://atcoder.jp/contests/arc176/submissions/52913935。