1043_二叉树的生成和遍历(循环方式)
1、遍历方法
- 前序遍历(preOrder)
- 对每个节点(子树)、贯彻这个遍历顺序:根 -> 左 -> 右
- 中序遍历(inOrder)
- 左 -> 根 -> 右
- 后序遍历(postOrder)
- 左 -> 右 -> 根
- 层序遍历
- 一层一层、从左到右遍历
参考资料:
二叉树各种遍历方法递归和循环实现
树的层次遍历的几种方法
2、构造
2.1、伪代码
前序遍历方式构造:
push(pRoot, stamp=FALSE) // pRoot指向根节点、但根节点还未创建
while(pop(pNode, stamp) == c_Stack_avilable):
if(stamp == FALSE):
pNode = new_node() // 创建节点
if(pNode != NULL): // 这个节点创建成功(亦即这个节点是存在的)
push(pRoot, stamp=TURE)
else:
push(pNode.rChild, stamp=FALSE)
push(pNode.lChild, stamp=FALSE)
end_while
优化(中序和后序不一定可以做类似的优化):
push(pRoot)
while(pop(pNode) == c_Stack_avilable):
pNode = new_node() // 创建节点
if(pNode != NULL): // 这个节点创建成功(也就是说:这个节点是存在的)
push(pNode.rChild)
push(pNode.lChild)
end_while
使用中序和后序遍历方式生成二叉树时、不一样的地方在于:将节点的左右孩子指针入栈之前,要先判断这个节点是否需要被创建。
比如、中序遍历方式:
push(pRoot, stamp=FALSE) // 指向根节点、但根节点还未创建
while(pop(pNode, stamp) == c_Stack_avilable):
if(stamp == FALSE):
if(pNode.has_rChild() == TURE):
push(pNode.rChild, stamp=FALSE)
if(pNode.has_lChild() == TURE):
push(pNode, stamp=TURE)
push(pNode.lChild, stamp=FALSE)
else:
pNode = new_node()
end_while
2.2、实际代码
// ========================================================================= //
// 二叉树节点数据
// ========================================================================= //
#define _none_node (0xFFFFFFFF - 10)
#define _N ((int)(_none_node)) // _N: 表示没有后继节点
// 准备 10 个节点的数据 + 叶子节点的 NULL数据(也就是_N)
static int data[] = { 1, 2, 3, _N, _N, 4, 5, _N, _N, _N,
6, 7, _N, _N, 8, 9, _N, _N, 10, _N, _N };
static Array_peek_t TreeData_peek =
{
.data = (void *)data,
.dataLen = sizeof(data[0]),
.size = _countof(data),
.index = 0,
};
// 准备 10 个节点
static Tree_t TreeNodes[10];
static Array_peek_t TreeNode_peek =
{
.data = (void *)TreeNodes,
.dataLen = sizeof(TreeNodes[0]),
.size = _countof(TreeNodes),
.index = 0,
};
// 取出数组元素,并返回剩余元素的数目(不可重入的函数)
void *Fun_Array_peek(pArray_peek_t pArray)
{
void *pData = Fun_Array_frontData(pArray);
if(pData == NULL)
{
return NULL;
}
pArray->index++;
return pData;
}
// ========================================================================= //
// 使用前序遍历方式生成二叉树
// ========================================================================= //
static void c_Tree_creat_node(p_Tree_t *pNode, pArray_peek_t pNodeData, pArray_peek_t pNodeAddr)
{
int *pData;
p_Tree_t newNode;
if(pNode == NULL) { return; }
pData = (int *)Fun_Array_peek(pNodeData);
if((pData == NULL) ||
(*pData == _none_node))
{
*pNode = NULL;
return;
}
newNode = (p_Tree_t)Fun_Array_peek(pNodeAddr);
if(newNode == NULL)
{
*pNode = NULL;
return;
}
newNode->data = *pData;
*pNode = newNode;
Tree_print_node_info_l_debug(pNode);
}
// 将根节点的地址作为参数传入初始化函数即可
void c_Tree_init_l(p_Tree_t *pTree, pArray_peek_t pNodeData, pArray_peek_t pNodeAddr)
{
p_Tree_t pNode = NULL;
if((pNodeData == NULL) || (pNodeAddr == NULL)) { return; }
memset(pNodeAddr->data, 0x00, pNodeAddr->size);
c_Stack_push(&Stack, (int)pTree);
while(c_Stack_pop(&Stack, (int*)&pNode) == c_Stack_avilable)
{
c_Tree_creat_node((p_Tree_t *)pNode, pNodeData, pNodeAddr);
pNode = *(p_Tree_t *)pNode;
if(pNode != NULL)
{
// Tree_print_node_l_debug(pNode);
c_Stack_push(&Stack, (int)&pNode->rChild);
c_Stack_push(&Stack, (int)&pNode->lChild);
}
}
}
// ========================================================================= //
// 测试
// ========================================================================= //
#if 1
static p_Tree_t pLamonTree = NULL;
void Funtest_Tree_l(void)
{
printf("\r\n\r\nFuntest Tree_l\r\n\r\n");
printf("pLamonTree @ %p\r\n", &pLamonTree);
c_Tree_init_l(&pLamonTree, &TreeData_peek, &TreeNode_peek);
printf("\r\n");
c_Tree_print_tree_text_l(pLamonTree);
c_Tree_preOrder_traverse_l(pLamonTree);
c_Tree_inOrder_traverse_l(pLamonTree);
c_Tree_postOrder_traverse_l(pLamonTree);
}
#endif
部分函数在其他文件、这里未提供。
完整代码:https://gitee.com/manon-des-sources/CppCodeLib/blob/master/Codes/c_Tree_l.c
3、遍历
伪代码
前序遍历:
push(pRoot, stamp=FALSE)
while(pop(pNode, stamp) == c_Stack_avilable):
if(stamp == FALSE):
push(pNode, stamp=TURE)
if(pNode.rChild != NULL):
push(pNode.rChild, stamp=FALSE)
if(pNode.lChild != NULL):
push(pNode.lChild, stamp=FALSE)
else:
print(pNode)
end_while
中序遍历:
push(pRoot, stamp=FALSE)
while(pop(pNode, stamp) == c_Stack_avilable):
if(stamp == FALSE):
if(pNode.rChild != NULL):
push(pNode.rChild, stamp=FALSE)
push(pNode, stamp=TURE)
if(pNode.lChild != NULL):
push(pNode.lChild, stamp=FALSE)
else:
print(pNode)
end_while
后序遍历:
push(pRoot, stamp=FALSE)
while(pop(pNode, stamp) == c_Stack_avilable):
if(stamp == FALSE):
if(pNode.rChild != NULL):
push(pNode.rChild, stamp=FALSE)
if(pNode.lChild != NULL):
push(pNode.lChild, stamp=FALSE)
push(pNode, stamp=TURE)
else:
print(pNode)
end_while
4、测试结果
[ Start test[Jul 4 2023, 17:30:26]: ====================================== ]
Funtest Tree_l
// 生成二叉树过程中的中间信息
pLamonTree @ 00410158
[pTree: 00410158] -> [(d: 004100E0 = 1), l: (004100E4 -> 00000000), (r: 004100E8 -> 00000000)]
[pTree: 004100E4] -> [(d: 004100EC = 2), l: (004100F0 -> 00000000), (r: 004100F4 -> 00000000)]
[pTree: 004100F0] -> [(d: 004100F8 = 3), l: (004100FC -> 00000000), (r: 00410100 -> 00000000)]
[pTree: 004100F4] -> [(d: 00410104 = 4), l: (00410108 -> 00000000), (r: 0041010C -> 00000000)]
[pTree: 00410108] -> [(d: 00410110 = 5), l: (00410114 -> 00000000), (r: 00410118 -> 00000000)]
[pTree: 004100E8] -> [(d: 0041011C = 6), l: (00410120 -> 00000000), (r: 00410124 -> 00000000)]
[pTree: 00410120] -> [(d: 00410128 = 7), l: (0041012C -> 00000000), (r: 00410130 -> 00000000)]
[pTree: 00410124] -> [(d: 00410134 = 8), l: (00410138 -> 00000000), (r: 0041013C -> 00000000)]
[pTree: 00410138] -> [(d: 00410140 = 9), l: (00410144 -> 00000000), (r: 00410148 -> 00000000)]
[pTree: 0041013C] -> [(d: 0041014C = 10), l: (00410150 -> 00000000), (r: 00410154 -> 00000000)]
// 打印整个二叉树
[d: 004100E0 = 1], [l: 004100E4 -> 004100EC(2)], [r: 004100E8 -> 0041011C(6)]
[d: 004100EC = 2], [l: 004100F0 -> 004100F8(3)], [r: 004100F4 -> 00410104(4)]
[d: 004100F8 = 3], [l: 004100FC -> 00000000(_N)], [r: 00410100 -> 00000000(_N)]
[d: 00410104 = 4], [l: 00410108 -> 00410110(5)], [r: 0041010C -> 00000000(_N)]
[d: 00410110 = 5], [l: 00410114 -> 00000000(_N)], [r: 00410118 -> 00000000(_N)]
[d: 0041011C = 6], [l: 00410120 -> 00410128(7)], [r: 00410124 -> 00410134(8)]
[d: 00410128 = 7], [l: 0041012C -> 00000000(_N)], [r: 00410130 -> 00000000(_N)]
[d: 00410134 = 8], [l: 00410138 -> 00410140(9)], [r: 0041013C -> 0041014C(10)]
[d: 00410140 = 9], [l: 00410144 -> 00000000(_N)], [r: 00410148 -> 00000000(_N)]
[d: 0041014C = 10], [l: 00410150 -> 00000000(_N)], [r: 00410154 -> 00000000(_N)]
// 三种遍历结果
1 2 3 4 5 6 7 8 9 10
3 2 5 4 1 7 6 9 8 10
3 5 4 2 7 9 10 8 6 1
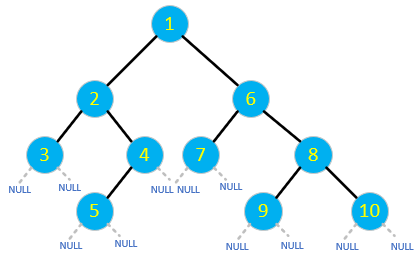
实际的二叉树:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号