Codeforces Round 1063 (Div. 2) 简解

CF2163A Souvlaki VS. Kalamaki

给一个长为 \(n\) 的序列 \(a\)，第 \(i\) 次操作为“交换元素 \(a_i\) 和 \(a_i\)，或者不做”，Alice 执行第奇数次操作，Bob 执行第偶数次操作。如果最后 \(a\) 序列不降，则 Alice 获胜。现在 Alice 可以在操作前将这个序列任意排列，问他能否必胜。

操作结束后的序列应该是 \(a\) 从小到大排序。直接将 \(a\) 排序，可以发现 Bob 执行一次操作后如果序列下降了，那么 Alice 是无法挽回的。所以只有所有 \(a_{2k}=a_{2k+1}\) 时，Bob 才不会让数列下降。

int Test;
int n,a[N],bot[N];
int main(){
	scanf("%d",&Test);
	while(Test--){
		scanf("%d",&n);int maxv=0;
		for(int i=1;i<=n;++i)bot[i]=0;
		for(int i=1;i<=n;++i){
			scanf("%d",&a[i]);
			maxv=max(maxv,a[i]);
			++bot[a[i]];
		}
		sort(a+1,a+1+n);
		bool flag=1;
		for(int i=2;i<=n-1;i+=2){
			if(a[i]<a[i+1])flag=0;
		}
		if(flag)puts("YES");
		else puts("NO");
	}
	return 0;
}

CF2163B Siga ta Kymata

给一个长为 \(n\) 的排列 \(p\) 和一个初始为 \(0\) 的长为 \(n\) 的二进制字符串 \(s\)。可以执行以下操作最多 \(5\) 次。

选择 \(l,r\) 满足 \(1\leq l\leq r\leq n\)，然后对于 \(i\) 满足 \(l<i<r\) 和 \(\min(p_l,p_r)<p_i<\max(p_l,p_r)\)，\(s_i\gets 1\)

然后给一个期望的01串 \(s'\)，若 \(s'_i=1\)，应有 \(s_i=1\)。问能否做到。

还是先求一下排列中每一个数的位置 \(loc_{p_i}=i\)

由于是排列，故没有重复的数，可以得到显然无解的情况：

\(s'_{loc_n}=1\) 或 \(s'_{loc_1}=1\)。表示最大或最小的数的位置无法变成 \(1\)。
\(s'_1=1\) 或 \(s'_n=1\)。表示最左或最右的位置无法变成 \(1\)。

进而可以发现答案就是 \([1,loc_{p_n}],[loc_{p_n},n],[1,loc_{p_1}],[loc_{p_1},n]\) 和 \([loc_{p_1},loc_{p_n}]\)（当然这个区间要调整使得左端点小于右端点）。证明的话，对于 \([1,loc]\) 中的数，将他的值和 \(p_1\) 比进行分类讨论即可。

scanf("%d",&n);
for(int i=1;i<=n;++i){
    scanf("%d",&p[i]);
    loc[p[i]]=i;
}
scanf("%s",s+1);
if(s[loc[1]]=='1'||s[loc[n]]=='1'||s[1]=='1'||s[n]=='1'){
    puts("-1");
    continue;
}
puts("5");
printf("%d %d\n",1,loc[1]);
printf("%d %d\n",loc[1],n);
printf("%d %d\n",1,loc[n]);
printf("%d %d\n",loc[n],n);
printf("%d %d\n",min(loc[1],loc[n]),max(loc[1],loc[n]));

fun fact：让 deepseek 给我翻译题面，然后他说把最后一个区间改成 \([1,n]\) 也可以，然后确实也可以。

CF2163C Monopati

给一个 \(2\times n\) 的网格图 \(a\)，\(a_{i,j}\in[1,2n]\)。定义 \(f(l,r)(1\leq l\leq r\leq 2n)\)，如果 \(a_{i,j}\in[l,r]\)，\(b_i\gets 1\) 否则 \(b_i\gets 0\)。然后问 \(b\) 是否存在一条右下路径（\(\forall b_{i,j}=1\)，且只能向右向下），若存在 \(f(l,r)=1\)，否则为 \(0\)。

现在求 \(\sum_{i=1}^{2n}\sum_{j=i}^{2n}f(i,j)\)。

显然如果 \(f(l,r)=1\)，则 \(f(l',r')=1(l'\leq l\and r\leq r')\)。然后显然路径共有 \(n\) 条，第 \(i\) 条为

\[(1,1)\to (1,2)\to \cdots(1,i)\to (2,i)\to\cdots(2,n-1)\to(2,n) \]

对第 \(i\) 条路径，他合法的条件就是 \(l\leq \min a\leq \max a\leq r\)，\(\min a\) 和 \(\max a\) 可以对第一行求前缀最大最小值，第二行求后缀最大最小值得到。

答案就是所有路径答案的并集。这玩意比较典，但是我代码比较唐就不挂了。

CF2164D Diadrash (Eazy/Hard Version)

交互题。

给一个长为 \(n\) 的值为 \([0,n-1]\) 的排列 \(p\)，给 \(q\) 个区间 \([l_i,r_i]\)，现在让你求这 \(q\) 个区间的最大 \(\text{MEX}\) 值。每次你可以询问一个连续区间的 \(\text{MEX}\) 值。

\(n\leq 10^4,q\leq 3\times 10^5\)

Eazy Verson

最多可以询问 \(\max(300,\lceil \frac{n}{2}\rceil+2)\) 次。

显然一个区间如果不包括 \(0\)，其 \(\text{MEX}\) 值为 \(0\)。那么如果我们能找到 \(0\) 的位置，则只需要查询包含这个位置的区间即可。记找到的 \(0\) 的位置为 \(loc\)

现在区间还是太多了，又可以发现如果一个区间严格包含另一个区间，那么被包含的区间的答案一定不会比包含区间的答案优。现在我们只用关心 ① \(l\leq loc\leq r\) ②不被其他区间包含的区间，可以发现这些区间的个数是小于等于 \(\min(loc,n-loc+1)\leq \lceil n/2\rceil\) 个的。

现在研究如何找 \(0\)，直接二分会用 \(\log n\) 次操作，不太行。同时我们可以发现 \(|loc-\lceil n/2\rceil|\) 越大，最后查询区间答案时查询的区间个数越少。找 \(0\) 时，第 \(i\) 次查询区间 \([n/2-i+1,n/2+i]\)，如果返回值 \(>0\)，那么说明区间内有 \(0\) 且在这次查询的区间两端（每次区间往左往右扩展一格），则再进行一次查询查 \([n/2-i+1,n/2+i-1]\) 即可知道是在左端还是右端。

那么总共的操作次数就刚好是 \(\lceil \frac{n}{2}\rceil+2\) 次。

int n,lef[N],rit[N],q;
inline int query(int l,int r){
	printf("? %d %d\n",l,r);
	fflush(stdout);
	int x;scanf("%d",&x);
	return x;
}
int main(){
	int Test;scanf("%d",&Test);
	while(Test--){
		scanf("%d%d",&n,&q);
		for(int i=1;i<=n;++i){
			lef[i]=0,rit[i]=n+1;
		}
		for(int i=1;i<=q;++i){
			int l,r;scanf("%d%d",&l,&r);
			lef[l]=max(lef[l],r);
			rit[r]=min(rit[r],l);
		}
		int l=n/2,r=n/2+1,loc=n;
		for(;l>=1&&r<=n;--l,++r){
			int x=query(l,r);
			if(x==0)continue;
			x=query(l+1,r);
			if(x==0)loc=l;
			else loc=r;
			break;
		}
		int ans=0;
		if(loc<=n-loc+1){
			for(int i=1;i<=loc;++i){
				if(lef[i]>=loc){
					ans=max(ans,query(i,lef[i]));
				}
			}
		}else{
			for(int i=loc;i<=n;++i){
				if(rit[i]<=loc){
					ans=max(ans,query(rit[i],i));
				}
			}
		}
		printf("! %d\n",ans);
		fflush(stdout);
	}
	return 0;
}

Hard Version

最多可以询问 \(30\) 次。

还是记 \(f(l,r)\) 为区间 \([l,r]\) 中所有数的 \(\text{MEX}\) 值。

还是先把所有不被其他区间包含的区间找出来，答案区间只能在这里面。显然这些区间满足，左端点递增的同时，右端点也递增。如图，横轴 \(i\) 表示区间编号，纵轴表示端点在排列序列上的位置，下黑线为左端点，上黑线为右端点。记 \(l_i,r_i\) 为第 \(i\) 个区间的左右断点。

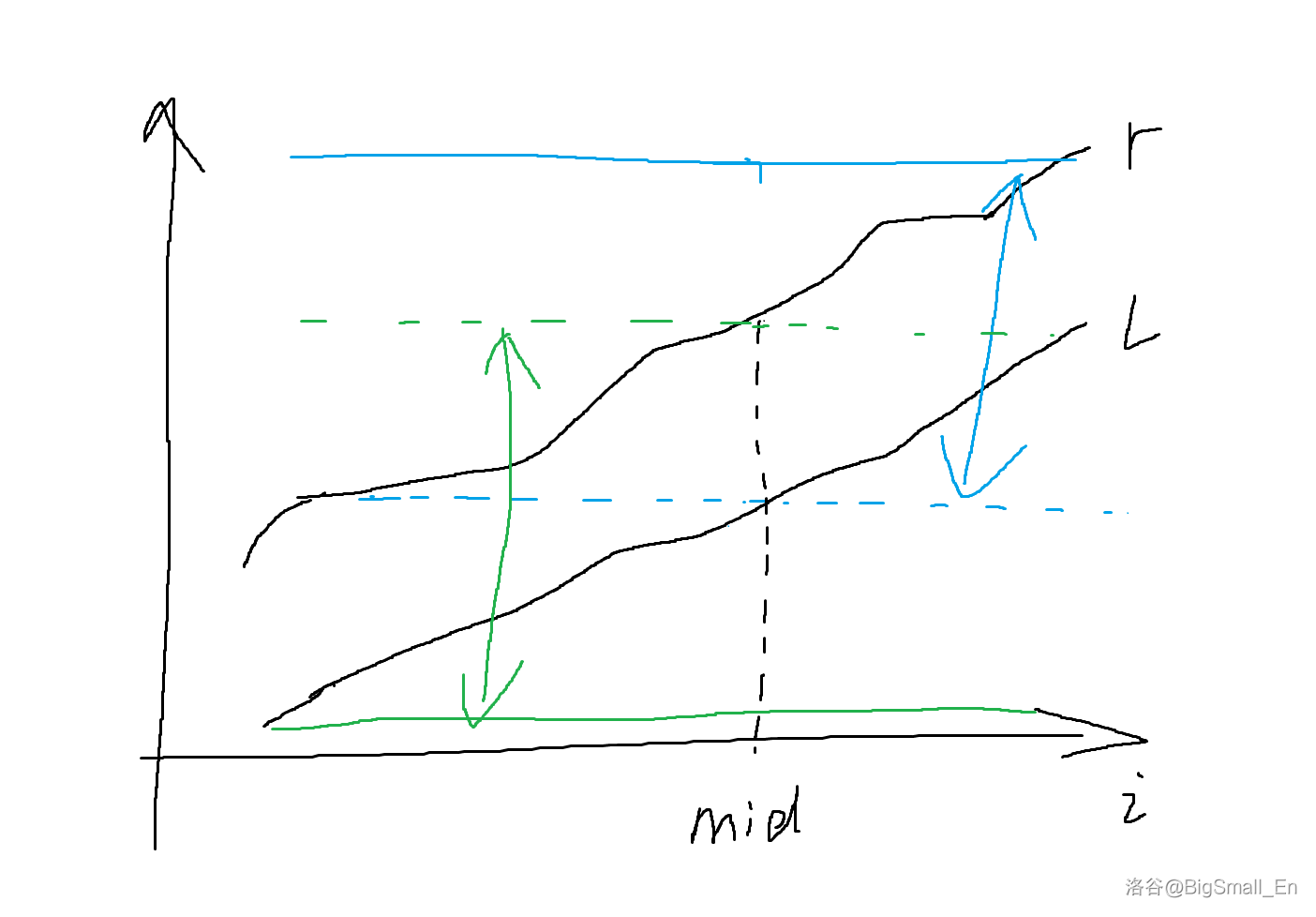
假设查询一个区间的 \(\text{MEX}\) 值为 \(x\)，意味着这个区间内包含 \([0,x-1]\) 的所有数。对于一个区间 \(p\)，现在再查询 \(f(1,r_p)=a,f(l_p,n)=b\)，那么区间 \([1,r_p]\) 包含 \([0,a-1]\)，区间 \([l_p,n]\) 包含 \([0,b-1]\)，他们都包含 \([0,f(l_p,r_p)-1]\)。如果 \(a> f(l_p,r_p)\)，那么意味着 \(f(l_p,r_p)\) 这个数在 \([1,l_p-1]\) 这个区间中，而不在 \([r_p+1,n]\) 这个区间中，那么 \(f(l_p,n)=f(l_p,r_p)\)；反之如果 \(b> f(l_p,r_p)\)，则 \(f(1,r_p)=f(l_p,r_p)\)，我们可以得出重要结论：

\[f(l_p,r_p)=\min(f(1,r_p),f(l_p,n)) \]

同时比较 \(f(1,r_p)=a,f(l_p,n)=b\)。若 \(a>b\)，那么所有 \(l>l_p\) 的区间都不会包含 \(f(l_p,r_p)\) 这个数，它们的答案始终 \(\leq f(l_p,r_p)\)，即 \(f(l_{p+k},r_{p+k})\leq f(l_p,r_p)\)；反之若 \(a<b\)，则有 \(f(l_{p-k},r_{p-k})\leq f(l_p,r_p)\)。那么我们现在就可以二分答案了。

写的时候没有发现上面的结论，但大致思想相同，故写得比较复杂，可以直接看题解的 implement。

int n,q;int mxr[N],lef[N],rit[N],tot;
inline int query(int l,int r){
	if(l>r)return -1;
	printf("? %d %d\n",l,r);
	fflush(stdout);
	int x;scanf("%d",&x);
	return x;
}
int main(){
	int Test;scanf("%d",&Test);
	while(Test--){
		scanf("%d%d",&n,&q);tot=0;
		for(int i=1;i<=n;++i)mxr[i]=0;
		for(int i=1;i<=q;++i){
			int l,r;scanf("%d%d",&l,&r);
			mxr[l]=max(mxr[l],r);
		}
		for(int i=1;i<=n;++i){
			if(mxr[i]&&mxr[i]>rit[tot]){
				lef[++tot]=i;
				rit[tot]=mxr[i];
			}
		}
		int l=1,r=tot,ans=1;
		while(l<r){
			int mid=(l+r)>>1;
			int up=query(lef[mid+1],n);
			int dw=query(1,rit[mid]);
			if(up>dw){
				l=mid+1,ans=mid+1;
			}else r=mid,ans=mid;
		}
		int val=query(lef[ans],rit[ans]);
		printf("! %d\n",val);fflush(stdout);
	}
	return 0;
}

CF2163E Plegma

有一个 \(n\times n\) 的二进制网格图，小 A 知道这个图长什么样并知道这个图是否联通（所有的 \(1\) 可以走相邻边到达），但他只能给小 B 传递这个网格图某一行和某一列的状态（字符串表示）。小 B 只知道 \(n\) 的大小和小 A 传递给他的某一行和某一列的状态，他需要知道这个图是否联通。保证图中至少有一个 \(1\)。

写一个程序扮演小 A 或小B，使得你的程序小A给的信息能让程序小B得出这个图是否联通。

分类讨论题。

假设传递的列信息第一位是 \(0\)，那么答案是联通，否则不连通。显然只有第一行不全为 \(0\) 或 \(1\) 才能进行。

如果第一行全为 \(1\)，且答案为联通，那么传递行信息全为 \(1\)；若答案不连通，则找一行含 \(0\) 的或全为 \(0\) 的传递。

如果第一行全为 \(0\)，且答案为不连通，那么传递列信息全为 \(0\)；若答案联通，则找一行含 \(1\) 的或全为 \(1\) 的传递。

具体实现见代码

char opt[N],s[N][N];
int n,C;
inline bool antique_line(int r){
	for(int j=2;j<=n;++j)
		if(s[r][j]!=s[r][j-1])return 0;
	return 1;
}
void solveA(){
	scanf("%d%d",&n,&C);int r=0,c=0;
	for(int i=1;i<=n;++i)scanf("%s",s[i]+1);
	if(antique_line(1)){
		for(int i=2;i<=n;++i){
			if(!antique_line(i)){
				r=i;
				break;
			}
		}
		if(r==0){
			for(int i=2;i<=n;++i){
				for(int j=1;j<=n;++j)
					if(s[i][j]!=s[1][1])
						r=i;
			}
		}
		if(s[1][1]=='0'){
			if(C==1)r=r,c=1;
			else r=1,c=1;
		}else{
			if(C==1)r=1,c=1;
			else r=r,c=1;
		}
	}else{
		r=1;
		for(int j=1;j<=n;++j){
			if(C==0&&s[1][j]=='1')c=j;
			if(C==1&&s[1][j]=='0')c=j;
		}
	}
	printf("%d %d\n",r,c);
}
void solveB(){
	scanf("%d",&n);
	scanf("%s%s",s[1]+1,s[2]+1);
	if(antique_line(1)){
		if(s[1][1]=='1')puts("1");
		else puts("0");
	}else{
		if(s[2][1]=='1')puts("0");
		else puts("1");
	}
}
int main(){
	scanf("%s",opt);
	int Test;scanf("%d",&Test);
	while(Test--){
		if(opt[0]=='f')solveA();
		else solveB();
	}
	return 0;
}

总结/后记

南京区域赛又打铜后的第一场CF，本来早上4点才到学校就睡了几个小时晚上困死了，但是想了想还是打了。前期速度还是有点慢，过C的时候都70分钟了，C写复杂了。其实这个交互不难，但是还是写得有点慢。最后performance 2043，看起来还可以但是还是达不到期望的高度。

这场题总体还是比较猜的感觉，尤其是数据范围猜答案，很多人都没过 B。D出得挺好的，E虽然纸面上不难但讨论清楚对于本菜鸡来说还是有点烧脑。

posted @ 2025-11-13 10:47 BigSmall_En 阅读(24) 评论(0) 收藏举报

刷新页面返回顶部

BigSmall_En