M. Managing Cluster 题解
M Managing Cluster 题解
给定一颗大小为 \(2n\) 的树,每个节点上都有 \(1\sim n\) 的一个数,每个数出现两次。
现在可以进行下列操作:选择两个从未进行过操作的节点,将上面的两个数交换。
如果一条树边连接的两个节点上的数相同,则收益 \(+1\),通过操作最大化最后收益。输出操作方案。
题解
感觉思维过程不太好写,就直接先猜后证吧。
首先,答案的上界一定是“每次用一条边覆盖树的两个未覆盖的点,最大的覆盖边数”,现在我们给出这些覆盖的边,只需要证明能一定能通过某种操作使得这些边两端的数相同。
我们将 \(n\) 个数分成三类:1. 不在任何一条覆盖边上;2. 在一条覆盖边上;3. 在两条覆盖边上。
同时我们可以将这些条覆盖边分成三类:
- 边的两端的数均只出现在这条覆盖边上。
- 边一端的数只出现在这条覆盖边上,另一端的数出现在两条覆盖边上。
- 边两端的数均出现在两条覆盖边上。
对于第一类边,处理是显然的(直接随便找一个不在边上但与边上一端数相同的数替换过来即可)。
对于剩下两类边,边与边之间通过相同的数产生联系(进而形成顺序),它们又可以构成两种情况
- 只有第三类边。
- 中间全是第三类边,两端为第二类边。
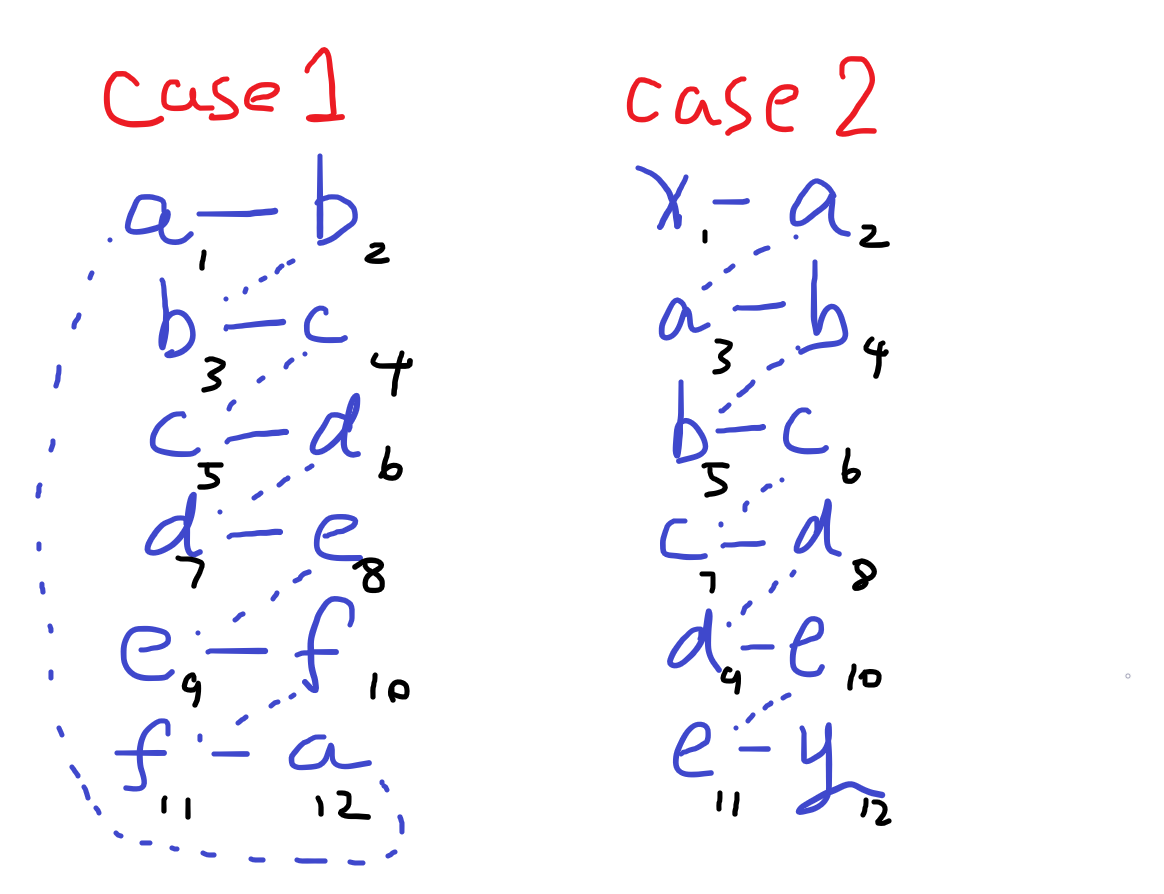
对于第一类情况。可以进行以下交换:\((2,12),(3,11),(4,10),(5,9),(6,8)\),即每次交换 \((1+i,2 n-i+1)\)。即可完成每条边上两端的数相同。
对于第二类情况。假设值与 \(x,y\) 相同但不在覆盖边上的点编号为 \(x',y'\)。先交换 \((2,x'),(3,y')\),将数 \(a\) 完全移出覆盖边,即可与第一类情况相同进行交换。此时每次交换 \((3+i,2n-i+1)\)。
按照上述策略进行交换,我们可以发现最终每条覆盖边两端的数都相同了。即取到了上界。
实现
找到覆盖边,我们可以使用一个比较简单的树形DP来实现。对于这些交换操作,我们可以建一张新图,将覆盖边两端的点在新图上连边,然后对于在两条覆盖边上出现的数对应的两个点连边。这样即可通过对新图 DFS 找到图示这样的“环”或“链”,进而进行操作。具体见代码。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int>ttfa;
const int N=300005;
const ll INF=0x3f3f3f3f3f3f3f3f;
int n,a[N],pos[N][2];
vector<int>tar[N];
int dp[N][2],son[N];
ttfa lis[N];int tot;
void dfs1(int u,int f){
for(auto v:tar[u]){
if(v==f)continue;
dfs1(v,u);
dp[u][0]+=max(dp[v][0],dp[v][1]);
}
for(auto v:tar[u]){
if(v==f)continue;
int tmp=dp[u][0]-max(dp[v][0],dp[v][1])+dp[v][0]+1;
if(tmp>dp[u][1]){
dp[u][1]=tmp;
son[u]=v;
}
}
}
void dfs2(int u,int p,int f){
if(f){
for(auto v:tar[u]){
if(v==p)continue;
dfs2(v,u,0);
}
}else{
if(dp[u][0]>=dp[u][1]){
for(auto v:tar[u]){
if(v==p)continue;
dfs2(v,u,0);
}
}else{
lis[++tot]={u,son[u]};
dfs2(son[u],u,1);
for(auto v:tar[u]){
if(v==p||v==son[u])continue;
dfs2(v,u,0);
}
}
}
}
bool vis[N];
int bot[N];
vector<int>lin[N];
ttfa ans[N];int cnt,stk[N],top;
bool cmp(ttfa x,ttfa y){
return bot[a[x.first]]+bot[a[x.second]]<bot[a[y.first]]+bot[a[y.second]];
}
void dfs(int rt,int u,int f){
if(vis[u])return;
vis[u]=1;
stk[++top]=u;
for(auto v:lin[u]){
if(v==f)continue;
dfs(rt,v,u);
}
}
int main(){
int Test;scanf("%d",&Test);
while(Test--){
scanf("%d",&n);tot=cnt=0;
for(int i=1;i<=2*n;++i){
tar[i].clear();lin[i].clear();
son[i]=dp[i][0]=dp[i][1]=0;
pos[i][0]=pos[i][1]=0;
vis[i]=0;bot[i]=0;
}
for(int i=1;i<=2*n;++i){
scanf("%d",&a[i]);
if(pos[a[i]][0])pos[a[i]][1]=i;
else pos[a[i]][0]=i;
}
for(int i=1;i<2*n;++i){
int u,v;scanf("%d%d",&u,&v);
tar[u].push_back(v);
tar[v].push_back(u);
}
dfs1(1,0);
dfs2(1,0,0);
//printf("%d\n",tot);
for(int i=1;i<=tot;++i){
//printf("lis: %d %d\n",lis[i].first,lis[i].second);
++bot[a[lis[i].first]];
++bot[a[lis[i].second]];
lin[lis[i].first].push_back(lis[i].second);
lin[lis[i].second].push_back(lis[i].first);
}
for(int i=1;i<=n;++i){
if(bot[i]==2){
lin[pos[i][0]].push_back(pos[i][1]);
lin[pos[i][1]].push_back(pos[i][0]);
}
}
sort(lis+1,lis+1+tot,cmp);
for(int i=1;i<=tot;++i){
if(a[lis[i].first]==a[lis[i].second])continue;
int x=lis[i].first,y=lis[i].second,z=0;
int xx=(pos[a[x]][0]==x?pos[a[x]][1]:pos[a[x]][0]);
int yy=(pos[a[y]][0]==y?pos[a[y]][1]:pos[a[y]][0]),zz=0;
if(bot[a[x]]+bot[a[y]]==2){
swap(a[y],a[xx]);
ans[++cnt]={y,xx};
continue;
}
if(bot[a[x]]>bot[a[y]]){swap(x,y);swap(xx,yy);}
top=0;int beg=2;
dfs(x,x,xx);
// printf("top: %d\n",top);
// for(int i=1;i<=top;++i){
// printf("%d ",stk[i]);
// }puts("");
if(bot[a[x]]==1){
z=stk[top];
zz=(pos[a[z]][0]==z?pos[a[z]][1]:pos[a[z]][0]);
swap(a[stk[2]],a[xx]);ans[++cnt]={stk[2],xx};
swap(a[stk[3]],a[zz]);ans[++cnt]={stk[3],zz};
beg=4;
}
for(int j=beg,k=top;j+2<=k;++j,--k){
swap(a[stk[j]],a[stk[k]]);
ans[++cnt]={stk[j],stk[k]};
}
}
printf("%d\n",cnt);
for(int i=1;i<=cnt;++i){
printf("%d %d\n",ans[i].first,ans[i].second);
}
}
return 0;
}
后记
可以说是微微改变世界线的一题?不懂喵,呜呜呜呵呵。不过赛事没严格想然后乱写终究还是战犯了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号