CF571A 题解

CF571A Lengthening Sticks

你有三根木棍，长度分别为 \(a,b,c\) （单位：厘米）。你可以选择把这些木棍加长一些长度，但是加长部分总和不能超过 \(l\) 厘米。现在给出 \(a,b,c,l\)，求有多少种加长的方案使得加上后的 \(a',b',c'\) 可以围成一个面积为正的三角形（即不能退化成线段或者为不成三角形）。

数据范围 \(1\leq a,b,c\leq 3\times 10^5,0\leq l\leq 3\times 10^5\)。

数学低手想不到容斥和 \(O(1)\) 做法，只能直接做了，实际上也并不难而且思路比较直接。

step1

首先我们枚举一条边 \(c\) 加长长度为 \(i\)，即先固定一条边的长度。则问题转化为

有三个木棍，长度分别为 \(a,b,c\)，可以对长为 \(a,b\) 的木棍加长一些长度，加长部分总和不能超过 \(l\)，满足三条木棍可以围成三角形。

（注意其中 \(c,l\) 的值与原题有所不同，它们均可以通过枚举的 \(i\) 计算出来）

现在我们假设长 \(a\) 的木棍加长 \(x\)，长 \(b\) 的木棍加长 \(y\)。先计算出 \(b+y\geq a+x\) 的情况下的答案，再计算出 \(b+y< a+x\) 情况下的答案。

step2

假设 \(b+y\geq a+x\)，可以得到以下若干个不等式

\[b+y\geq a+x\\ x+y\leq l\\ c-(a+x)< b+y< c+(a+x)\\ x\geq 0,y\geq 0 \]

整理成直线的形式，并改写 \(<,>\) 为 \(\leq,\geq\)，可以得到

\[\begin{cases} y\geq x+a-b\\ y\leq x+c+a-b-1\\ y\geq -x+c-a-b+1\\ y\leq -x+l\\ x\geq 0\\ y\geq 0 \end{cases} \]

则理论上我们平面上满足这些条件的整点 \((x,y)\) 个数即可。这个玩意可以使用半平面交解决。

step3

由于我是计算几何低手，不会半平面交、皮克公式，也不会分类讨论求面积，只能看看有没有其他方法了。

一个朴素的想法是对于每个 \(x\)，求一个 \(y\) 的范围区间，这个区间可以根据约束条件 \(O(1)\) 求得，这样就可以枚举 \(x\) 求了。

我们真的需要枚举每个 \(x\) 吗？答案显然是否定的。我们将上面若干条直线（即半平面对应直线）的所有交点求出来，然后交点的按横坐标 \(x\) 排序，容易发现相邻的两个横坐标之间，\(y\) 的范围大小是一个等差数列（挺显然的，可以自己画一下）。由于横坐标知道，等差数列的项数知道，又两端的 \(y\) 范围大小也知道，即等差数列首项末项均知道，则可以直接求和公式算出来两个横坐标直接有多少点满足条件。然后枚举两个相邻的横坐标即可。

可能说的比较抽象，这个示意图意会一下吧，将夹在 \(l_1,l_2,l_3,l_4,x=0,y=0\) 的面积按横坐标分成 \(4\) 块。

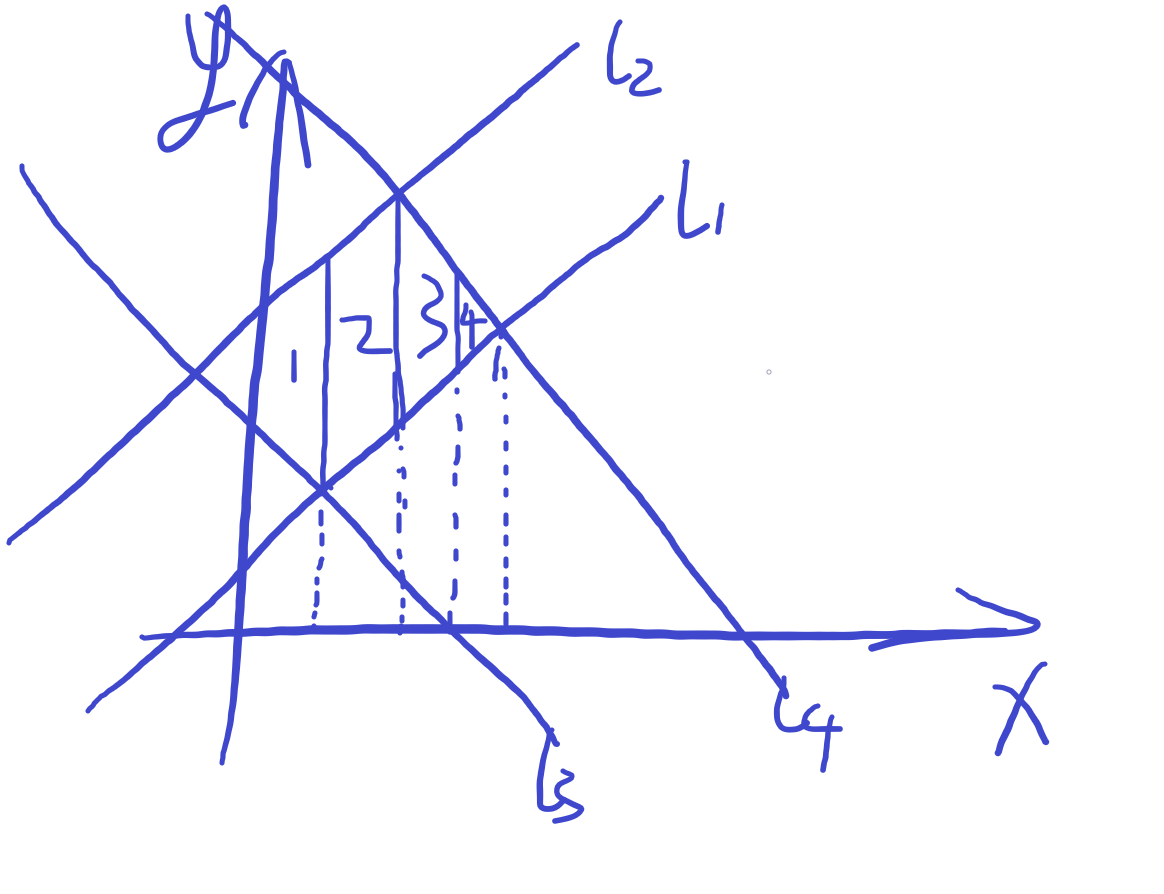
最后

现在我们计算好了 \(b+y\geq a+x\) 的情况，对于 \(b+y<a+x\) 的情况，只需要改变一个约束条件即可同理做。

交点的个数最多为 \(8\) 个是常数，因此复杂度为 \(O(l)\)。

实现

代码的变量名定义和题解中不太一样，参考即可，提交记录。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef pair<int,int>ttfa;
const int N=1000006;
const int INF=0x3f3f3f3f;

inline ll calc(ll a,ll b,ll c,ll d){
	auto dw=[a,c](ll x){return max(max(x+a,-x+c),0ll);};
	auto up=[b,d](ll x){return min(x+b,-x+d);};

	if(b<a||c>d)return 0;
	vector<ll>lis;
	lis.push_back(-a);
	lis.push_back(-b);
	lis.push_back(c);
	lis.push_back(d);
	lis.push_back((c-a)/2ll);
	lis.push_back((d-a)/2ll);
	lis.push_back((c-b)/2ll);
	lis.push_back((d-b)/2ll);
	sort(lis.begin(),lis.end());
	lis.erase(unique(lis.begin(),lis.end()),lis.end());
	lis.erase(lis.begin(),upper_bound(lis.begin(),lis.end(),0));
	ll len=up(0)-dw(0)+1,las=0,ans=0ll;
	if(len>0)ans+=len;
	len=up(1)-dw(1)+1,las=1;
	for(auto x:lis){
		ll lenx=up(x)-dw(x)+1ll;
		if(lenx>0){
			if(len>0)ans+=(len+lenx)*(x-las+1)/2ll;
			else ans+=lenx;
		}
		len=up(x+1)-dw(x+1)+1ll,las=x+1;
	}
	return ans;
}

inline ll solve(ll x,ll y,ll v,ll s,ll opt){//opt=0 x>=y; opt=1 x>y
	ll a=y-x+opt;
	ll b=v+y-x-1;
	ll c=max(max(v-x-y+1ll,0ll),a);
	ll d=s;
	return calc(a,b,c,d);
}
int main(){
	ll x,y,z,l;scanf("%lld%lld%lld%lld",&x,&y,&z,&l);
	ll ans=0;
	for(ll i=0;i<=l;++i){
		ans+=solve(y,z,x+i,l-i,0);
		ans+=solve(z,y,x+i,l-i,1);
	}
	printf("%lld\n",ans);
	return 0;
}