10 月杂题
1.CF1976F Remove Bridges
树的根度数为 \(1\),先开始树上每条边都是割边,连接根和叶子可以去掉更多的割边,先连接一个叶子和根,然后另外的叶子两两组合,每次肯定删去更多的点,删去一部分点后有些删去的就会减少,想到长链剖分,第一次选最大的,后面每次选两个最大的即可。
2.ABC374G Only One Product Name
如果 \(S_j\) 能接在 \(S_i\) 后面,那么 \(i\rightarrow j\),建完这个图,发现有环,环显然是可以缩成一个点的,问题就转化成了 DAG 的最小路径覆盖(可交)。先算不可交的,将每个点拆成入点和出点,如果 \(u,v\) 有边,那么从 \(u\) 的入点连向 \(v\) 的出点,那么入点出点天然的构成了一个二分图,假定先开始有 \(n\) 条路径,那么在二分图上连接一条边,等价于原图减少了一条路径,二分图最大匹配时覆盖路径最小,问题转化为二分图最大匹配。然后处理可交的问题,用传递闭包处理一下,算一下哪些点能到达,然后就跟上面一样。
3.CF1895F Fancy Arrays
容斥用 \(\min a_i\le x+k-1\) 的方案数减去 \(\max a_i<x\) 的方案数,第一个用最小值和差分数组算,最小值有 \(x+k\) 种,由于差分数组天然决定了数组的大小关系,所以差分数组的方案数为 \((2\times k+1)^{n-1}\),乘法原理相乘即可。第二种情况由于 \(x\) 很小可以直接暴力 dp,但是 \(n\) 太大所以要用矩阵优化。贡献 \(1\) 减去贡献 \(2\) 即为答案。
4.CF1860F Evaluate RBS
\((x,y)\) 是一个二元不好处理,考虑消元:\(ax+by=y(a\times \frac{x}{y}+b)\),全部同时除以 \(y\),那么 \(a\) 即为 \(k\),\(b\) 即为 \(b\),\(\frac{x}{y}\) 即为自变量,由此转化为一元关系,并且将每个元组变成了直线,\(n\) 条直线产生 \(n^2\) 个交点,将这些交点记录下来,并按照从大到小排序,会发现自变量在交点左侧,交点上以及右侧都能确定两条直线的 \(y\) 大小,也即顺序,所以从左到右移动交点,并且维护直线的 rank,括号匹配的充要条件是前缀最小值大于等于 \(0\),且和为 \(0\),用线段树维护前缀和即可。
5.CF1849F XOR Partition
每次找到全局最小异或对,将它们连边,表示它们不能在同一个部分,一棵树天然决定了一个集合的划分,所以问题转化为求异或的 MST,这个就是板子了:有一个叫 Boruvka 的算法就是用来解决完全图的生成树问题,算法大致就是把所有点当成一个连通块,然后每个连通块找到外部最小的边,然后连上,问题在于如何找到外部最小的边,即求最小异或值,直接使用 0/1 trie 即可。最后得到了树黑白染色即可。
6.CF1841F Monocarp and a Strategic Game
答案具有单调性可以二分,假定现在 check \(p\),枚举题中所给的左右分界处,问题就变成了左右选最多的数满足和 \(\le p\) 并且和 \(\ge k\),本来我是用主席树实现的,复杂度为 \(\mathcal{O}(b\log^2 V)\),被卡常了过不了,所以改成了堆。
7.CF1814F Communication Towers
看到时间一眼线段树分治,但是这个是点,不是板子,一个小技巧把它变成加边,每条边加入的时候看它的两个点交集的事件,但是这个我竟然没想到。然后就是正常的线段树分治,难点在于可撤销并查集的处理。正常操作的并查集后,在每个时间节点也就是叶子,对 \(1\) 所在的连通块标价 \(+1\),然后在进行并查集回退的时候子节点加上原来的贡献,不过为了避免前面有些本来有标记,所以合并的时候提前减一下,这样就可以保证增量是对的了。
8.P11189 「KDOI-10」水杯降温
很好的题啊,可以这么构造:使用若干次 \(2\) 操作,让 \(w_{fa_i}\ge w_i\) 并且 \(w_1\le 0\),过后就可以直接用 \(1\) 操作达到目的,可以证明这个是充要条件。那么问题就转化为了在满足 \(w_{fa_i}\ge w_i\) 的情况下最多能进行多少次 \(1\) 操作,并判断这个数量与原始 \(w_1\) 的大小关系,第一种无解情况就是 \(w_{fa_i}<w_i\),这个是比较好判断掉的。然后就 dp,设 \(f_u\) 表示 \(u\) 子树内最多能进行多少次 \(2\) 操作,这个玩意儿不是很好转移啊,但是 \(f_u\) 的值是具有单调性的,就是说 \(f_u\) 越大越不容易满足,所以可以二分,记二分的答案为 \(p\),设 \(t_v=w_u-w_v\) 表示于这棵子树外最多能进行多少次 \(2\) 操作,那么 \(\max(0,p-t_v)\) 即为 \(v\) 至少能做多少次操作,然后把这些相加,看是否有 \(p\),还要判一下子节点的 \(f\) 相加有没有 \(p\),尝试简单说一下这个为什么是对的,终态 \(f_u\) 肯定是由各个儿子合起来的,每一个儿子要么是本身次数顶满了,要么是别的儿子顶满了,所以都取一个至少,就能让前面所说的两个条件顶满。
9.BZOJ4423 Bytehattan
如果题目不强制在线肯定倒序加边就秒了,强制在线就需要用到对偶图。
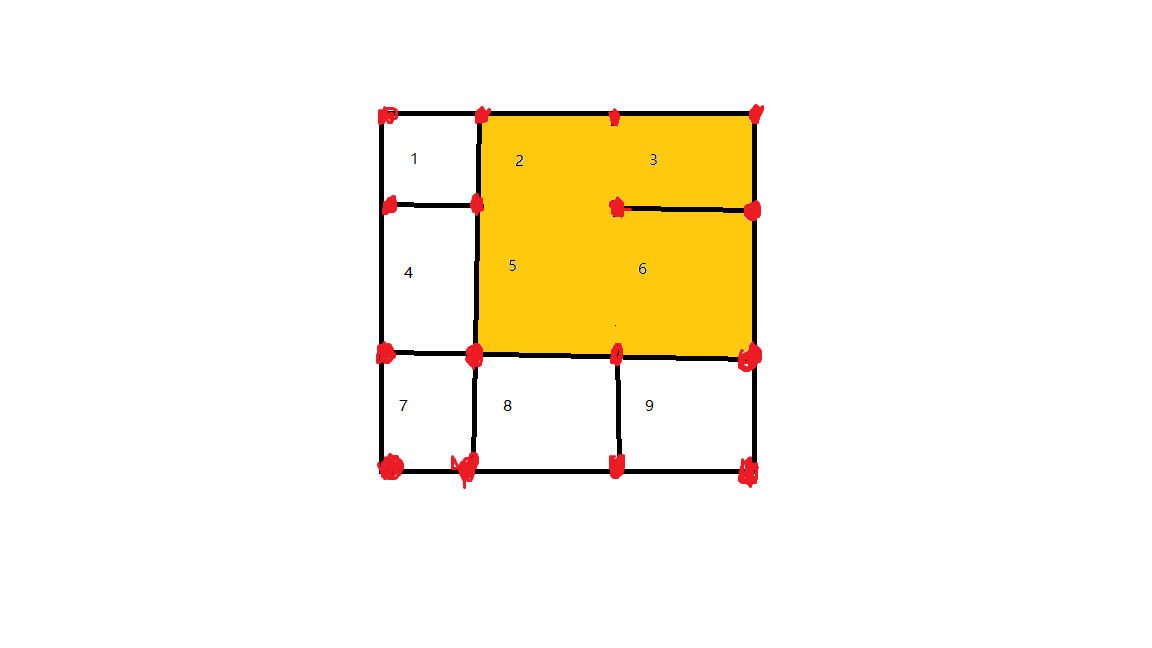
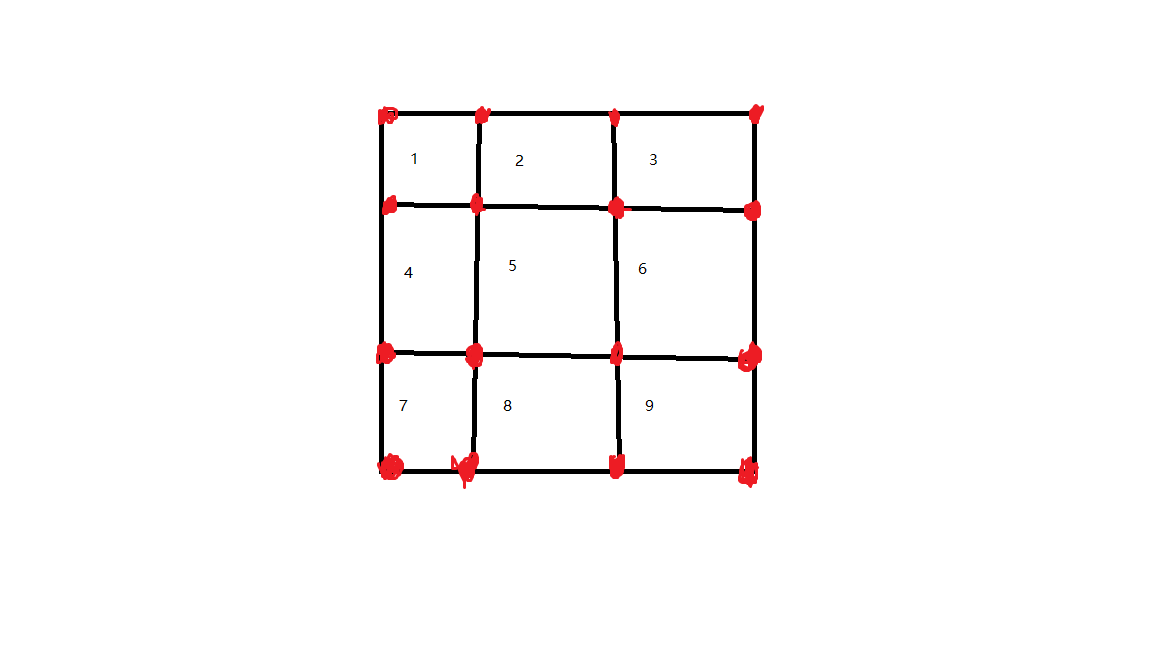
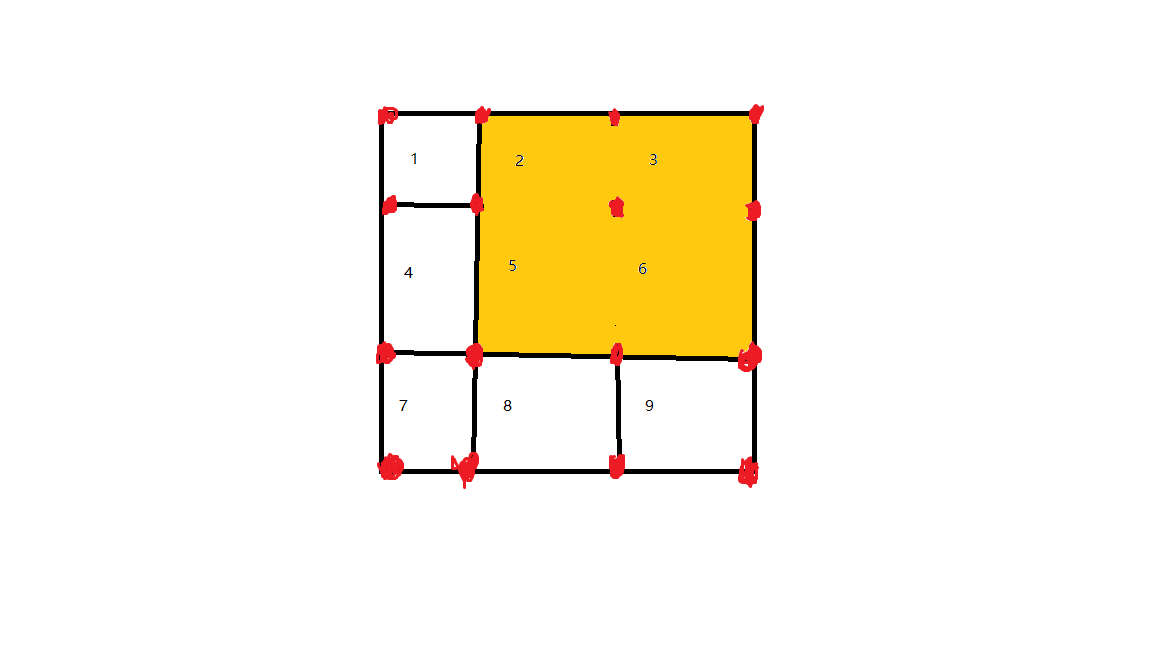
如图,题中图上的点实际为红点,记录格子里的点,初始格子里的点不连通,当删除一条边时,如果边两侧的格子已经联通,那么删除这条边后,就会使图上的点不连通,否则合并即可。
10.「HNOI 2018 省队集训 Day 5」party
好题。先思考已经确定每个人到终点的路径的颜色种类的情况,将人和颜色看成两部,人的一部为左部,然后将人进行拆点,每个人拆的数量一样,问让左部匹配完左部最多有多少个点,这个就涉及到了霍尔定理。
- Hall 定理:设二分图 \(G\) 的两部分别为 \(V_L,V_R\) 且 \(|V_L|\le|V_R|\),则其存在一个大小为 \(V_L\) 的匹配当且仅当 \(\forall S\subseteq V_L\),都有 \(|S|\le|\cup_{v\in S} N(v)|\)
问题相当于求这个最大的 \(V_L\),那么直接枚举子集 \(S\),然后求得 \(\min\{\frac{|\cup_{v\in S} N(v)|}{|S|}\}\) 即可。回到原题,找最近的点等于找这一堆点的 LCA,然后路径上的种类数量使用 树剖+ 线段树 + bitset 即可。
11.P3488 [POI2009] LYZ-Ice Skates
印象中这道题以前牛客模拟赛考过,当时觉得还出的挺好的,结果是原。人与鞋子进行匹配,转到二分图上去,即判断左部是否能完备匹配,根据 hall 定理的结论找子集,此处比较特殊子集可以找连续的区间,简单说明一下为什么区间是对的,因为如果选的子集不是区间,即不连续,中间有空位置,但是选鞋子的区间始终跟左右端点有关系,所以中间这些空位选上就能顶满,推式子。
右边是一个常数,即只用判断左边最大值是否小于等于右边即可,查询最大子段和,判断即可。
12.P7307 [COCI2018-2019#1] Teoretičar
最小答案是最大的度数,观察到这个 \(2^k\),很让人不联想到分治。对边进行分治,表示对这些边进行划分,划分与最大度数有关,如果最大度数减半那么就满足分治结构,所以我们的分治目标就是把边集分成两个集合,两个集合颜色互不相同,两个集合内部待定。当分治到最大度数为 \(1\) 的时候,就不需要继续处理了。如何将两个集合颜色化为不同,可以根据分治层数 \(d\),一边加上 \(2^d\),一边不加,天然做到了颜色的划分,至于分边,将左边的奇点,右边奇点分别连一个汇点,跑欧拉回路,就可以做到边染色,时间复杂度做到了 \(\mathcal{O}((n+m)\log m)\),比较卡常。
13.P11191 「KDOI-10」超级演出
对每一个 \(a_i\) 求出如果 \(a_i\) 能够走到 \(1\),至少从哪个 \(l\) 开始,并记为 \(w_i\),查询区间 \([l,r]\) 也就变成了一个二维数点问题。求 \(w\) 变成了问题的瓶颈(难度上的)。使用阈值分治,每个初度 \(<B\) 的点,暴力遍历出点,求一下 \(\max\),更新完一个点后,再去暴力更新出度 \(\ge B\) 的点,复杂度为 \(\mathcal{O}(nB+n\times \frac{n}{B})\),平衡一下就是根号,然后就是二维数点问题,十分之经典的问题。
14.MX-S4-T2 youyou 不喜欢夏天
套路,先想一下后手会把交换操作用在哪些列上,肯定是一列只有一个,并且选的是 \(1\),另一个是 \(-1\),这样交换过后产生 \(-2\) 的贡献,称这种情况为「容易交换的」,假设选了 \(x\) 列「容易交换的」,最后的答案会减去 \(2\times \min(x,m)\),启示分开计算,第一种是选了「容易交换的」数量未达上限,后手会改成 \(-2\),所以先手直接对于一黑一白全选,这样贡献就是 \(0\),第二种情况,就正常 dp,但是因为假设了「容易交换的」数量超过上限,所以最后 dp 答案减去 \(2\times m\),两者取 \(\max\),至于 dp,很简单的 上/下/上下/不选 问题。
15.P9731 [CEOI2023] Balance
应该是 12 的即使训练,依旧是分治加上欧拉回路,分治的目的是每一次把每种颜色放进两堆列中,让两堆的该颜色数量差不超过 \(1\),这么一直分治到最底层,就可以保证所有列的某种颜色数量差不超过 \(1\),可以发现欧拉回路往往在这类问题中充当一个染色的任务,即分开。\(a_{i,j}\rightarrow i,a_{i,j}\leftarrow i\),然后建立虚拟原点向度数为奇数的点连边,保证能跑出来欧拉回路,假设只有一种颜色,这个欧拉回路有什么意义,让该颜色实现了均分(有可能多一个)在两边,从而实现了颜色在分治区间的均分,问题缩减了规模,复杂度为 \(\mathcal{O}(nS\log S)\),常数很大。
16.CF213E Two Permutations
审题要仔细,子序列和排列,如果是子串的话就比较简单,对差分进行哈希即可,可以根据排列这个特点判断出 \(b\) 中选取的子序列值域上是连续的,所以动态维护连续的子序列的哈希值,使用线段树,用哈希的一个式子 \(f(S+T)=f(S)\times p^{|T|}+f(T)\) 左右儿子维护即可,动态维护的过程就是移动指针,比较简单。
17.CF504E Misha and LCP on Tree
重链剖分把 \(a\rightarrow b,c\rightarrow d\) 的路径提取出来,二分最长公共前缀,然后哈希判一下相不相等,这样是 \(\mathcal{O}(n\log^2n)\),cf 直接给卡没了,优化当然也比较简单,枚举 \(\log\) 条链,先把能匹配的先匹配了,最后有一段匹配不了的直接用二分,这样就不用对 \(\log\) 条链进行二分了,时间复杂度为 \(\mathcal{O}(n\log n)\),还有一个原来不知道的坑点,就是 hash 的 base 要开过字符集,不然容易冲突,所以为什么,这是无从知晓的。
18.ABC343G Compress Strings
先去掉严格包含的,按照长度排序,然后枚举是否有比它大的包含它,hash 即可。剩下的字符串肯定互不包含,记录 \(g_{i,j}\) 表示 \(S_i\) 后面接 \(S_j\) 能重合多少个,转化为最多能重合多少个,但是这个为什么是对的,万一有的重复了包含另一个呢?举一个例子 xab,bcd,abc,发现 xabcd 实际上已经包含 abc,但是这个过程又可以看成 xab 后接 abc,abc 后又接 bcd,重合总数为 \(4\),总长度减去重合长度即为答案。这个理解完就比较好做了,\(f_{S,i}\) 表示 \(S\) 集合的已经包含完了,并且最后一个接的是 \(i\),枚举 \(j\),然后更新即可:\(f_{S+2^j,j}\gets \max\{f_{S,i}+g_{i,j}\}\),时间复杂度比较抽象,应该是 \(\mathcal{O}(n^2\sum l+n^22^n)\),可以通过。
19.CF1466G Song of the Sirens
假定 \(|s_0|\ge |w|\),记 \(f_{S}\) 表示字符串 \(S\) 包含多少个 \(w\),并记 \(s_0\) 前 \(|w|\) 个位置为 \(s_1\),后 \(|w|\) 个位置为 \(s_2\),递推解决这个问题:
相当于是后缀与加入字符与前缀产生的贡献,\(s_1,s_2\) 都是定值,而 \(t_i\) 不同的数量不超过 \(26\),那这个是可以暴力找出来的,记 \(g_x\) 表示插入成 \(s_2+x+s_1\) 的贡献,式子转化为:
把递推写成通项形式:
还是用 \(t_i\) 不同数量只有 \(26\) 个的性质,统计每一个字母产生的贡献,式子就不细写了。另外有 \(s_0<|w|\) 的情况,就把 \(s_0\) 先操作几次,然后再做,所以后面好像是只能用前缀和了。
20.CF986F Oppa Funcan Style Remastered
因数可以转化成质因子,即若干个质因子相加,将 \(k\) 进行质因数分解,分类讨论,如果质因子个数为 \(1\),直接判 \(n|d\),如果质因子个数为 \(2\),相当于判断 \(ax+by=n\) 是否有解,并且要求解为非负数,反正是随便做,然后就是质因子个数 \(\ge 3\) 的情况,这个情况相较于前两个比较特殊的地方是最小质因子 \(\le 10^5\),用同余最短路解决,同余最短路的思想就是钦定一个模数 \(p\),求 \(dis_{i\bmod p}\),意思是跟某个数同余,再用 \(p\) 进行补充,目标是 \(n\) 肯定就是与 \(n\) 同余,即判断 \(dis_{n\bmod p}\le n\) 即可,但是此题非常卡常,筛质数要用非常优秀的方法。
21.P2371 [国家集训队] 墨墨的等式
同余最短路很套路,设 \(dis_i\) 表示 \(a_{2\sim n}\) 的数进行组合得到 \(s\bmod a_1=i\) 的最小 \(s\),如果是求小于等于某个特定的数,直接就是 \(\sum_{i=0}^{a_1-1}\frac{h-dis_i}{a_1}+1\),这个题是 \([l,r]\),转化为 \(s(r)-s(l-1)\),非常套路。
22.CF1887C Minimum Array
假设有一全零序列 \(a\),另有一序列 \(b\) 与 \(a\) 比较字典序大小,字典序大小就取决于 \(b\) 的第一个非零位置的数的正负性,将该命题进行扩展,假定现在最小字典序答案序列为 \(a\),另有一序列 \(b\),如何比较 \(a,b\) 字典序大小,记 \(c_i=b_i-a_i\),发现可以转化为命题 1。回到原问题,把当前最优序列看成 \(a\),\(b\) 为此时正在操作进行的序列,并且把最优序列看成全 \(0\) 序列,当前序列因为只用看第一个非 \(0\) 数,所以可以直接用差分,用线段树动态判断第一个非 \(0\) 数的正负性即可。
23.CF1209E2 Rotate Columns (hard version)
肯定至多只会选 \(\max\) 前 \(n\) 大的列,这个比较显然,然后这个 \(m\) 就被降到了与 \(n\) 同阶,设 \(f_{i,S}\) 表示前 \(i\) 列钦定了状态为 \(S\) 行的最大值,考虑转移,首先预处理出当状态为 \(T\) 时第 \(i\) 列能产生的最大贡献,暴力枚举转了多少圈,然后就是转移:\(f_{i,S}\gets f_{i-1,T}+w_{S-T},T\subset S\),就是很常规的 dp 枚举最后一列的状态,然后转移前面,答案为 \(f_{\min(n,m),2^n-1}\),重点说一下正确性,万一选的那个不是最大值,那就不是最优的,而最优的方案一定是选了最大值的方案。
24.P8349 [SDOI/SXOI2022] 整数序列
想 \(\log\) 的做法愣是想不出来,传统的 \(\log\) 维护的是序列上的东西,这个东西跟序列甚至不沾边,最朴素的暴力就是把两种颜色合并到一起,枚举一个维度,然后另一维开数组记录一下,找 \(\max\) 即可,这个复杂度是跟两种颜色数量相关的,考虑阈值分治,记 \(c_i\) 表示第 \(i\) 种颜色的数量:
- \(c_u\le B,c_v\le B\)
此时直接暴力即可,复杂度为 \(\mathcal{O}(B)\),比较轻松。
- \(c_u>B,c_v>B\)
由于这样的颜色很少,这种条件的本质不同询问一样少,所以暴力完记录一下答案即可,复杂度总的为 \(\mathcal{O}(\frac{n^2}{B})\),也比较轻松。
最难的就是一大一小的情况了,钦定 \(c_u\le c_v\),利用 \(c_u\le B\) 这个条件入手,就是说能产生贡献的 \(v\) 实际上也只有 \(\mathcal{O}(B)\) 个,每个 \(a_i=u\) 找到它相邻的且没有被标记过的 \(a_j=v\),然后将 \(j\) 打上标记,加入总的序列,这样能保证总的序列长度是 \(\mathcal{O}(B)\) 级别的,再暴力就是对的了,不过注意到选择的 \(a_j=v\) 可能是不连续的,需要分开处理每一段。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号