数论分块

模板

即求 \(\sum_{i=1}^{n}\lfloor\frac{n}{i}\rfloor\)的值

\(y=n/i的图像\)

奇妙题解

参考

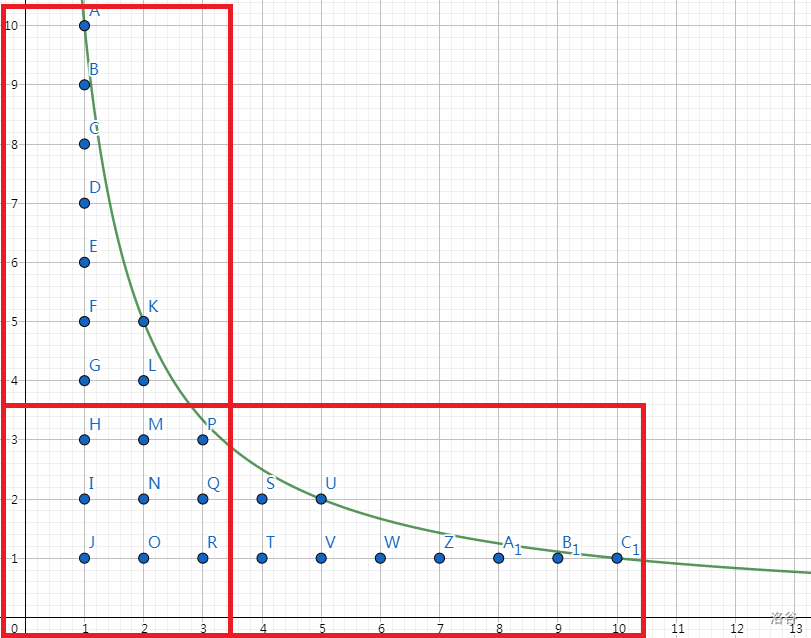
\[\Large\sum_{i=1}^{n}\lfloor\frac{n}{i}\rfloor=2\sum_{i=1}^{\lfloor\sqrt{n}\rfloor}\lfloor{\frac{n}{i}\rfloor-\lfloor\sqrt{n}\rfloor^2} \]

int h(cs int x)
{
	int s=sqrt(x),re=0;
	for(ri int i(1);i<=s;++i) re+=x/i;
	return re*2-s*s;
}

(还没验证正确性
upd10.29:AC

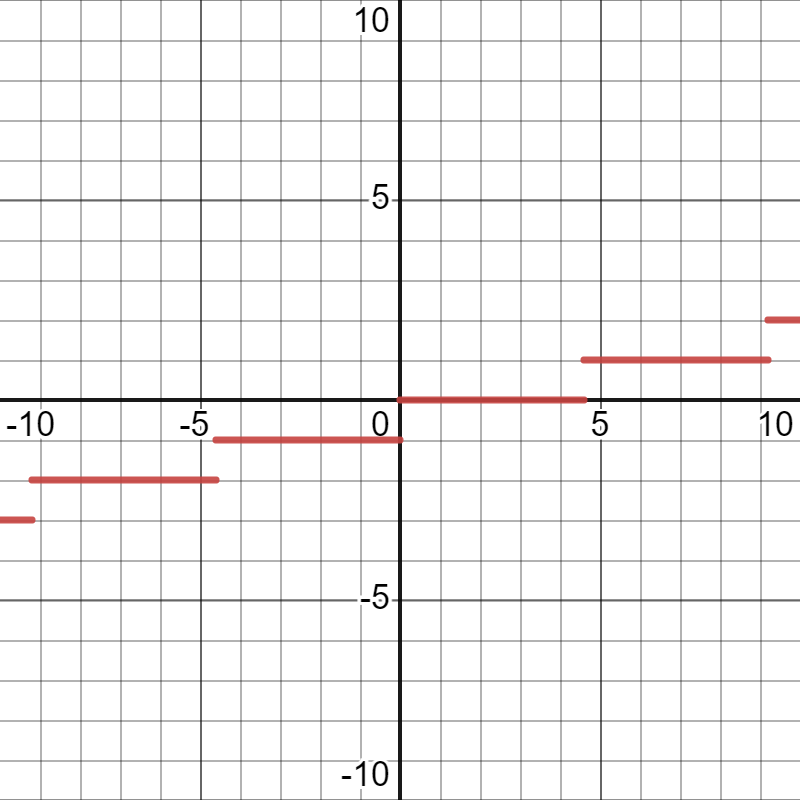
一般化

参考

某段数满足：

\[\because\lfloor\frac{n}{l}\rfloor=\lfloor\frac{n}{l+1}\rfloor=\lfloor\frac{n}{l+2}\rfloor=…=\lfloor\frac{n}{r-1}\rfloor=\lfloor\frac{n}{r}\rfloor \]

\[\therefore\lfloor\frac{n}{l}\rfloor\le\frac{n}{r}<\lfloor\frac{n}{l}\rfloor+1 \]

\[\therefore{r}\le\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor,r_\max=\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor \]

\[\therefore\sum_{i=l}^{r}f(\lfloor\frac{n}{i}\rfloor)=(\lfloor\frac{n}{\lfloor\frac{n}{l}\rfloor}\rfloor-l+1)\times\lfloor\frac{n}{l}\rfloor \]

int h(cs int x)
{
	if(!x) return 0;
	int re=0,j;
	for(ri int i(1);i<=x;i=j+1)
		j=x/(x/i),re+=(j-i+1)*(x/i);
	return re;
}

P2261 [CQOI2007]余数求和

参考

\[ans=\sum_{i=1}^{n} k\mod i \]

\[\because a\mod{b}=a-b\times\lfloor\frac{a}{b}\rfloor \]

\[\therefore ans=\sum_{i=1}^{n}k-i\times\lfloor{\frac{k}{i}}\rfloor=n\times{k}-\sum_{i=1}^{n}i\times{\lfloor\frac{k}{i}\rfloor} \]

然后整除分块

signed main()
{
	read(n),read(k);
	for(ri int l(1),r;l<=n;l=r+1)
	{
		if(k/l) r=min(k/(k/l),n);
		else r=n;
		ans-=(k/l)*(r-l+1)*(l+r)>>1;
	}
	wt(ans+n*k);
	return 0;
}