20230703测试
A
我不打了,但是考场上没想起来排列 stl 怎么写,所以在下面打 10 遍
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
next_permutation
你可以数一下,一共有 11 遍
B

\([1,1000]\)
典,对于这类数字和的题,直接考虑拆位处理,预处理一下就可以了
const int maxN = 1000 + 10;
int n;
string s[maxN];
int a[maxN][maxN];
int pre[maxN];
void solve(){
cin >> n;
fp(i, 1, n) cin >> s[i];
fp(i, 1, n) fp(j, 1, n) a[i][j] = s[i][j - 1] - '0';
int num = 1;
pre[0] = 1;
fp(i, 1, n) {
(num *= 10) %= mod;
pre[i] = (pre[i - 1] + num) % mod;
}
int ans = 0;
fp(i, 1, n) {
fp(j, 1, n) {
int x = (a[i][j] * pre[n - i]) % mod;
(x *= i) % mod;
(ans += x) %= mod;
x = (a[i][j] * pre[n - j]) % mod;
(x *= j) % mod;
(ans += x) %= mod;
}
}
cout << ans << endl;
}
C

\(n\in [1,20]\)
讲个笑话,老师发的代码过不去第一个样例……
还有个笑话,有个写了 D 的人 C 过不去
考场上想贪心想到头疼,正解是 DP ……
所以告诉我们,贪心没有正确性时,可以考虑 DP
一眼状压,但是我们不能直接枚举最终状态,考虑转移
我们目前已经将一些水杯中的水倒到了其他水杯中,然后考虑继续转移,可以将一杯水倒到另一个非空的杯子里进行更新
所以做完了
我是煞笔
const int maxN = 100, N = 1e7;
int n, m;
int f[N];
int c[maxN][maxN];
int popcount(int now) {
int sum = 0;
while (now) sum++, now -= (now & -now);
return sum;
}
void solve(){
n = rd(), m = rd();
fp(i, 1, n) fp(j, 1, n) c[i][j] = rd();
memset(f, 0x3f, sizeof(f));
if (m == n) {
cout << 0 << endl;
return ;
}
f[0] = 0;
int ans = inf;
fp(i, 1, (1 << n) - 1){ // black is k
fp(j, 1, n)
if (i & (1 << (j - 1))) // j to k
fp(k, 1, n)
if (!(i & (1 << (k - 1))))
f[i] = min(f[i], f[i ^ (1 << (j - 1))] + c[j][k]);
if (popcount(i) == n - m)
ans = min(ans, f[i]);
}
cout << ans << endl;
}
D

\(1e5\)
不太难
很明显,有重复的只可能出现在投票的组之中,可以对投票的组算一下每个人会有多少对重复的组,然后减出来就可以了
const int maxN = 1e5 + 10;
int n, m;
pii a[maxN],ts[maxN],mat[maxN]c[maxN];
map<pii, int> vis, mp;
inline int lowbit(int x) { return x & -x; }
inline void add(int wh) {for (; wh <= n; wh += lowbit(wh)) c[wh]++;}
inline int query(int x) {
if (x <= 0) return 0;
int sum = 0;
while (x) sum += c[x], x -= lowbit(x);
return sum;
}
void solve(){
cin >> n >> m;
fp(i, 1, n) {
cin >> a[i].first >> a[i].second;
ts[a[i].first]++, ts[a[i].second]++;
mp[a[i]]++;
mp[{a[i].second, a[i].first}]++;
}
fp(i, 1, n) {
if (vis[a[i]] || vis[{ a[i].second, a[i].first }]) continue;
vis[a[i]] = 1;
int x = a[i].first, y = a[i].second;
if (ts[x] + ts[y] - mp[a[i]] < m)
if (ts[x] + ts[y] >= m)
mat[x]++, mat[y]++;
}
fp(i, 1, n) add(ts[i] + 1);
int p = 0;
fp(i, 1, n) {
int sum = ts[i];
int k = n - query(m - sum);
if (ts[i] * 2 >= m) k--;
p += k - mat[i];
}
cout << p / 2 << endl;
}
E

好题
这里着重来讲一下转移的细节
不难想到,阶段的划分在于最后一对匹配上的点,所以可以用 \(f_{i,j}\) 来表示对上面前 \(i\) 个,下面前 \(j\) 个元素进行匹配的最大值
这里有两种转移,一种是不匹配直接摆烂,另一种是匹配,这两种转移相互独立
明显,要是匹配,那一定要找最近的两组
但……直接枚举匹配组好像有些困难,因为另外一组一点信息也没有
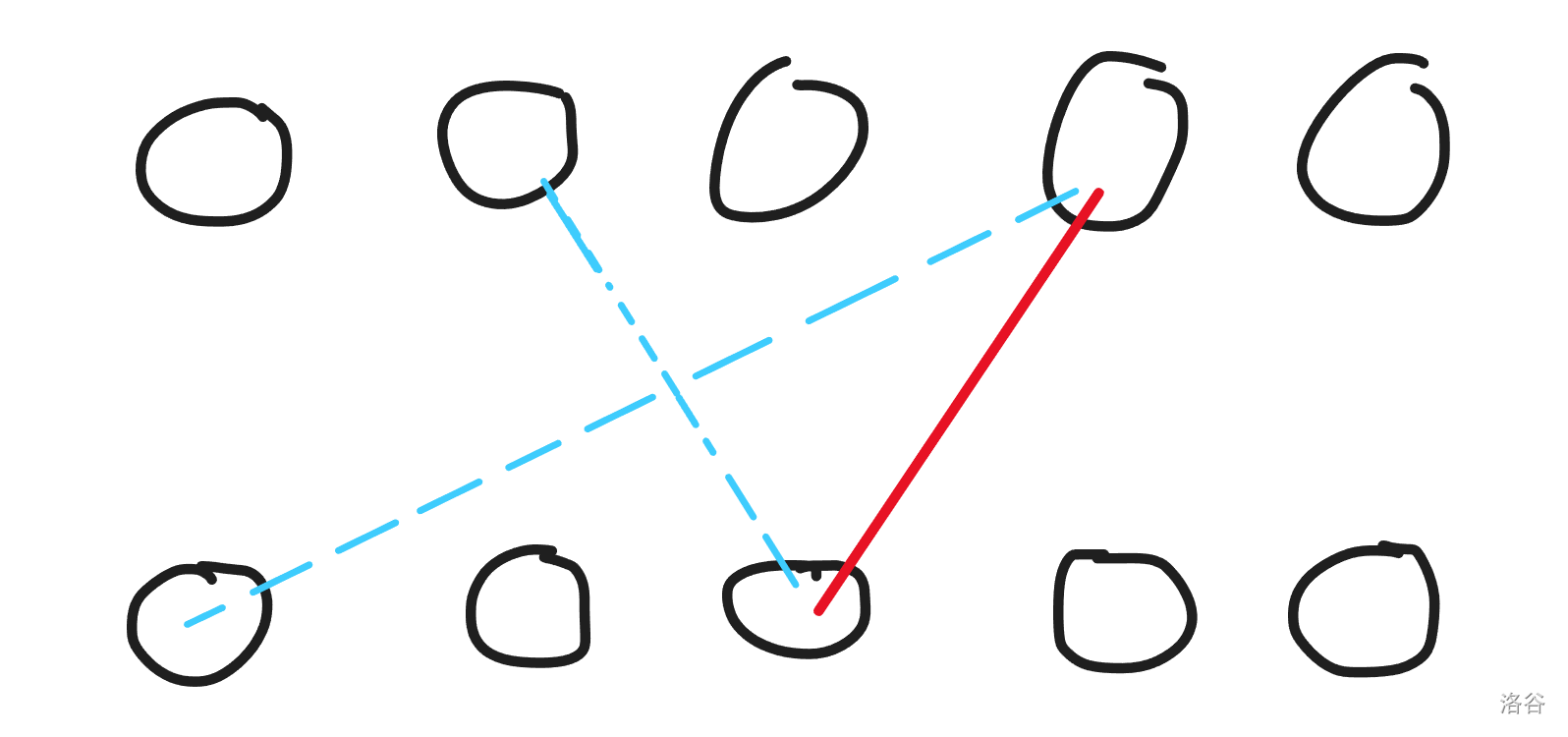
枚举一条红边,则蓝边是一定相交的
那就好办了,直接在 vector 上二分就可以了
const int maxN = 4000 + 10;
vector<int> p1[maxN * 2], p2[maxN * 2];
int n, m;
int a[maxN], b[maxN];
int f[maxN][maxN];
int last(vector<int> v, int x) {
if (v.empty())
return 0;
auto i = lower_bound(v.begin(), v.end(), x);
if (i == v.begin())
return 0;
i--;
return *i;
}
void lis() {
vector<int> v;
fp(i, 1, n) v.eb(a[i]);
fp(j, 1, m) v.eb(b[j]);
sort(v.begin(), v.end());
int len = unique(v.begin(), v.end()) - v.begin();
while (v.size() != len) v.pop_back();
fp(i, 1, n) a[i] = lower_bound(v.begin(), v.end(), a[i]) - v.begin() + 1;
fp(j, 1, m) b[j] = lower_bound(v.begin(), v.end(), b[j]) - v.begin() + 1;
}
void solve(){
n = rd(), m = rd();
fp(i, 1, n) a[i] = rd();
fp(i, 1, m) b[i] = rd();
lis();
fp(i, 1, n) p1[a[i]].eb(i);
fp(i, 1, m) p2[b[i]].eb(i);
int ans = 0;
vector<int> v;
auto x = v.begin();
fp(i, 1, n) {
fp(j, 1, m) {
f[i][j] = max(f[i][j - 1], f[i - 1][j]);
if (a[i] == b[j])
continue;
int lj = last(p2[a[i]], j);
int li = last(p1[b[j]], i);
if (!lj || !li)
continue;
f[i][j] = max(f[i][j], f[li - 1][lj - 1] + 2);
ans = max(f[i][j], ans);
}
}
cout << ans;
}
F
这题分两个解法
- CDQ
加入这个问题是静态的,那该怎么办?
并不难,我们可以开一个树状数组,暴力把所有的蜜饼扫一遍,加入树状数组中
那 CDQ 怎么做?可以对于总时间来进行排序,然后先更新左边,再更新右边就可以了
两只 \(\log\)
没写
- 线段树
我的写法和其他的不大一样,比较奇怪
以大小为下标,储存最小的时间
然后对于一次查询,我们将整个区间拆成几个小区间,然后从左到右判断是否子树里面有符合要求的蜜饼,有就直接进去取出来
还挺好写的,不得不说拆分区间真的牛
const int maxN = 2 * 1e6 + 10;
struct node {
int minx[maxN << 1], son[maxN << 1][2], lx[maxN << 1], rx[maxN << 1], maxx[maxN << 1];
int idx = 1, root = 1;
vector<int> v;
void pa() { met(minx, 0x3f), met(maxx, 0); }
void insert(int &now, int l, int r, int wh, int x) {
if (!now)
now = ++idx;
lx[now] = l, rx[now] = r;
if (l == r) {
minx[now] = min(x, minx[now]), maxx[now] = wh;
return;
}
int mid = (l + r) >> 1;
if (wh <= mid)
insert(son[now][0], l, mid, wh, x);
else
insert(son[now][1], mid + 1, r, wh, x);
minx[now] = min(minx[son[now][0]], minx[son[now][1]]);
maxx[now] = max(maxx[son[now][0]], maxx[son[now][1]]);
}
void split(int now, int l, int r, int ql, int qr) {
lx[now] = l, rx[now] = r;
if (ql <= l && r <= qr) {
v.eb(now);
return;
}
int mid = (l + r) >> 1;
if (mid >= ql)
split(son[now][0], l, mid, ql, qr);
if (qr > mid)
split(son[now][1], mid + 1, r, ql, qr);
}
int get_min(int now, int tim) {
if (lx[now] == rx[now])
return lx[now];
if (minx[son[now][0]] <= tim)
return get_min(son[now][0], tim);
else
return get_min(son[now][1], tim);
}
} seg;
int n, q;
void solve(){
cin >> n >> q;
seg.pa();
while (q--) {
char c;
cin >> c;
int x, a;
cin >> x >> a;
if (c == 'M')
seg.insert(seg.root, 1, n, a, x);
else {
seg.v.clear();
seg.split(1, 1, n, a, n);
int k = 0;
for (int y : seg.v)
if (seg.minx[y] <= x) {k = y; break;}
if (!k) cout << "-1" << endl;
else cout << seg.get_min(k, x) << endl;
}
}
}
G
\(k^2\) 是一个十分难以直接处理的条件,但是这个条件,却给了一个处理的范围
明显,\(f_i\) 为对于这个前缀,枚举一个前缀进行转移,但是这个枚举区间有一个限制:如果颜色数大于\(\sqrt{n}\),则一定不是最优的
所以我们就有了一个 \(O(n\sqrt{n})\) 的做法
这里使用链表来处理这个问题
这里的链表不省空间
const int maxN = 5 * 1e4 + 10, B = 250;
int n;
int a[maxN], f[maxN];
int last[maxN];
struct node {
int nex[maxN], pre[maxN];
void init() {
pre[0] = -1;
fp(i, 1, n) pre[i] = i - 1, nex[i] = i + 1;
}
void del(int x) {
nex[pre[x]] = nex[x];
pre[nex[x]] = pre[x];
}
} list;
void lis() {
vector<int> v;
fp(i, 1, n) v.eb(a[i]);
sort(v.begin(), v.end());
int len = unique(v.begin(), v.end()) - v.begin();
while (v.size() != len) v.pop_back();
fp(i, 1, n) a[i] = lower_bound(v.begin(), v.end(), a[i]) - v.begin() + 1;
}
void solve(){
while (scanf("%d", &n) != EOF) {
fp(i, 1, n) scanf("%d", a + i);
lis();
met(f, 0x3f);
f[0] = 0;
list.init();
fp(i, 1, n) {
if (last[a[i]])
list.del(last[a[i]]);
last[a[i]] = i;
int sum = 0;
for (int j = list.pre[i]; j != -1; j = list.pre[j]) {
sum++;
if (sum >= 250)
break;
f[i] = min(f[j] + (sum * sum), f[i]);
}
}
printf("%d\n", f[n]);
memset(f, 0, sizeof(f));
memset(last, 0, sizeof(last));
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号