Codeforces Round 870 (Div. 2)
A. Trust Nobody
有人认为第一题太难了,但我觉得还好吧
你要是打了前天的 CN-Round 就知道什么是真正的难了
方法很简单,我们枚举一下所有可能的说谎人数,然后记一下有多少人声称的人数大于了这个数,如果两个数相同,那就输出,如果没有就输出 No
void solve(){
int n;
int a[200];
cin >> n ;
fp(i,1,n) cin >> a[i];
for(int i=0;i<=n;++i){
int cnt=0;
for(int j=1;j<=n;++j){
if(a[j]>i)
++cnt;
}
if(cnt==i) {
cout << i << endl;
return ;
}
}
cout << "-1" << endl;
}
Lunatic Never Content
现在有一个数组 \(a\),和 \(n\) 个非负整数,定义 \(f(a,x)=[a_1\bmod x,a_2\bmod x,\dots,a_n\bmod x]\),其中 \(x\) 为正整数。现要你找到最大的 \(x\),使得 \(f(a,x)\) 是回文的。
数据保证 \(\sum n \leq 10^5\)。
这题不难,我们有方程 \(a_i \equiv a_j \pmod{x}\),则有 \(a_i-a_j \equiv 0 \pmod{x} \Leftrightarrow x\mid (a_i-a_j)\)
那就好办了,我们找到最大公约数就可以了,若其本身就是回文的,就是无穷大
inline ll gcd(int a,int b){
if(!b) return a;
return gcd(b,a%b);
}
const int maxN=1e5+10;
ll a[maxN],n;
void solve(){
cin >> n;
for(int i=1;i<=n;++i) cin >> a[i];
int flag=1;
for(int i=1;i<=n;++i)
if(a[i]!=a[n-i+1]) flag=0;
if(flag){
cout << 0 << endl;
return ;
}
vector<ll> v;
for(int i=1;i<=n;++i)
v.push_back(max(a[i],a[n-i+1])-min(a[i],a[n-i+1]));
int len=unique(v.begin(),v.end())-v.begin();
while(v.size()!=len) v.pop_back();
ll ans=v[0];
for(int i=1;i<v.size()-1;++i)
ans=gcd(ans,v[i]);
cout << ans << endl;
}
C. Dreaming of Freedom
明显,只要在\([2,m]\)中有一个数能整除\(n\),则投票结束,这里直接质因数分解判断最小质因子就可以了
这题放T3明显不合适,也不知道出题人怎么想的
int n,m;
void solve(){
n=rd(),m=rd();
int p=n;
vector<int>v;
for(int i=2;i*i<=n;++i){
if(p%i==0) v.push_back(i);
while(p%i==0) p/=i;
if(p==1) break;
}
if(p!=1) v.push_back(p);
if(n==1) {
cout << "YES" << '\n';
return ;
}
if(v[0]<=m) cout << "NO" << '\n';
else cout << "YES" << '\n';
}
D. Running Miles
给定一个长度为 \(n\) 的数列 \(a\),请找出其中的一个区间 \([l,r]\),最大化区间内的前三大值之和与 \(r-l\) 的差,并求出这个值。
\(n\in[3,1e5],a_i\in[1,1e8]\)
这里我在考场上推出了一个性质,就是我们倾定右端点,则最优的左端点的位置是单调不减的
但是这个性质看上去很强,但是实际上屁用没有,这里引用四边形不等式学习笔记中的一句话
对于普通的决策单调性 DP,只能保证最终的决策点是单调的
也就是说,我们这里可以保证最后的决策点是单调的,但是为了验证这个决策点,我们可能需要将左指针向右跳很多步才可以验证,所以这个性质没有用
正解这里使用了区间性问题的经典解法,枚举中间,我们枚举三个城市中间的那一个,则可以将贡献拆成 \(a_i-l\) 和 \(a_j+r\) ,我们直接算出这个贡献就可以了
明显,这里算出来的贡献可能不符合条件,但这样明显更劣,所以不会影响结果
这里用了两个 set 来算,实际上也可以做个前后缀优化为 \(O(n)\)
const int maxN=1e5+10;
ll a[maxN],n;
void solve(){
n=rd();
fp(i,1,n) a[i]=lrd();
multiset<pll> s1,s2;
ll ans=0ll;
fp(i,3,n)
s2.insert({a[i]-i,i});
fp(i,2,n-1){
s1.insert({a[i-1]+i-1,i-1});
auto p1=s1.rbegin(),p2=s2.rbegin();
ll t1=p1->first,t2=p2->first;
ans=max(ans,t1+t2+a[i]);
s2.erase(s2.lower_bound({a[i+1]-i-1,i+1}));
}
cout << ans << endl;
}
E. Walk the Runway
你要带着 \(n\) 个模特去参加 \(m\) 场演出,第 \(i\) 名模特的出场会给你带来\(p_i\)的收益,每场演出对每个模特有一个评分,模特出场有顺序,要求每次出场的模特评分单调递增,求最大收益。
\(n\in[1,5000],m\in[1,500]\)
其实我一直有一个疑问,就是bitset究竟能在什么时候能够优化复杂度,于是我做了一个测试
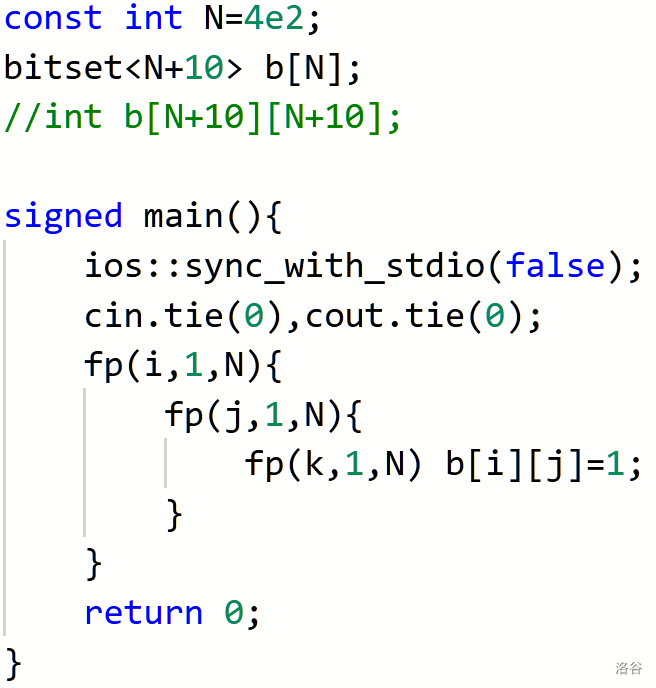
用时 1348ms
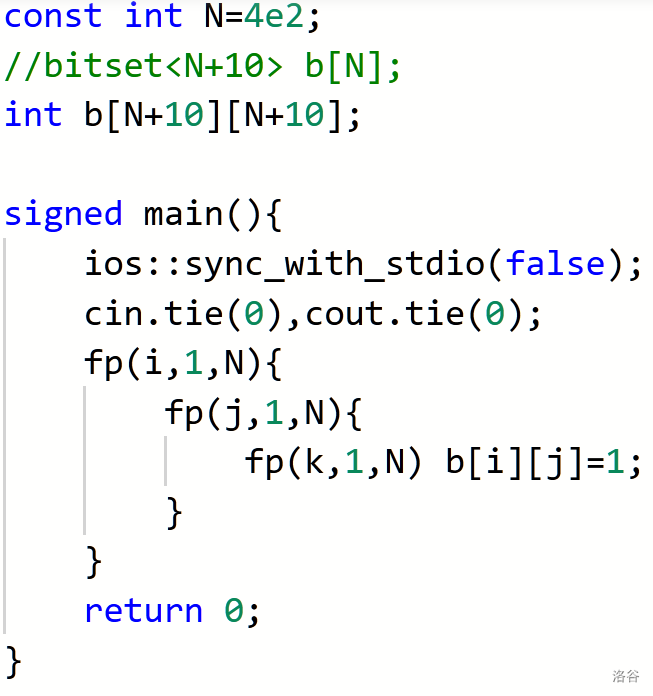
用时 121ms
这个问题可能是因为当bitset出现了重复赋值的时候可能会出现效率极其低下的可能,但总体来说,bitset 只能在其特有运算时优化复杂度,单纯地用 bitset 替换掉数组可能并没有太大的作用
话说回来,我们这道题看上去并没有什么特别靠谱的解法去做,所以做法就较为极端
维护任意两个模特之间的偏序关系,表示一个模特可不可以在另一个模特之前出现,这明显是一个 Dag ,所以这里可以想想假如是单调不减怎么办
然后对着这个 Dag 跑最长路就可以了,这好像是一个很典的东西
但问题是这里暴力去做是 \(O(n^2m)\) 的,这里我们想到了 bitset ,我们排个序,对于每个模特开个 bitset ,然后发现这里转移可以直接继承上一个模特的状态,然后这里可以直接把一个模特所有场的状态给与起来就可以了
其实就是一个高维偏序的板子
复杂度除上一个 \(w\)
极度卡常,至少对于我来说,开足了优化还是卡着时限过的,可能我人型自走大常数
#pragma GCC optimize(2)
#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <map>
#include <unordered_map>
#include <set>
#include <bitset>
#define ll long long
#define fp(a,b,c) for(ll a=b;a<=c;a++)
#define fd(a,b,c) for(ll a=b;a>=c;a--)
#define pii pair<int,int>
#define pll pair<ll,ll>
#define fr first
#define sd second
#define mod 1000000007
#define inf 0x3f3f3f3f
using namespace std;
inline int rd(){
int x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9')x = (x<<1) + (x<<3) + (ch^48),ch = getchar();
return x * f;}
inline ll lrd(){
ll x = 0, f = 1;char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}
while(ch >= '0' && ch <= '9')x = (x<<1) + (x<<3) + (ch^48),ch = getchar();
return x * f;}
const int maxN=5000+10,N=500+10;
int n,m;
bitset<5010> cal[maxN],basis;//对于每一个点来做
bitset<5010> suf[maxN],res[maxN];
int p[maxN],a[N][maxN];
ll dis[maxN];
int in[maxN];
ll ans=0;
vector<int> g[maxN];
void topo(){
queue<int> q;
memset(dis,0,sizeof(dis));
fp(i,1,n){
if(!in[i])q.push(i);
dis[i]=p[i];}
while(!q.empty()){
int temp=q.front();
ans=max(ans,dis[temp]);
q.pop();
for(int i=1;i<=n;++i){
int x=i;
if(!res[temp][i]) continue;
in[x]--;
dis[x]=max(dis[x],dis[temp]+p[x]);
if(in[x]==0)
q.push(x);
}
}
}
signed main(){
m=rd(),n=rd();
fp(i,1,n) p[i]=rd();
fp(i,1,m)
fp(j,1,n)a[i][j]=rd();
fp(i,1,n) res[i].set();
fp(i,1,m){
vector<pii> v;
fp(i,1,n) cal[i].reset();
fp(j,1,n)v.push_back({a[i][j],j});
sort(v.begin(),v.end());
fd(j,v.size(),1){
suf[j]=suf[j+1];
suf[j][v[j-1].second]=1;}
int last=n;
cal[v.back().second].reset();
fd(j,v.size()-1,1){
while(v[last-1].first!=v[j-1].first) --last;
cal[v[j-1].second]=suf[last+1];
}
fp(j,1,n) res[j]=(res[j]&cal[j]);
}
fp(i,1,n)
fp(j,1,n)
if(res[i][j])
in[j]++;
topo();
cout << ans << '\n';
return 0;
}
经过实际测试,上面这份代码现在已经卡不过去了,有时间我重构一份,但是大概率是没有时间

 浙公网安备 33010602011771号
浙公网安备 33010602011771号