W1

A

水省

B

明显，我们如果要让方差最小，一定是取平均数，我们这里取上取整和下取整算一下就行

这里多枚举了几个数

#include <iostream>
#include <string>
#include <string.h>
#define int long long
#define ull unsigned long long

using namespace std;
const int maxN = 1e5 + 10;
int a[maxN], n;

int myceil(int x, int y) {
    if (x % y == 0)
        return x / y;
    else
        return (x + y) / y;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n;
    int sum = 0;
    for (int i = 1; i <= n; ++i) cin >> a[i], sum += a[i];
    int down = sum / n;
    int res = 0x7ffffffffffff;
    for (int k = -2; k <= 2; ++k) {
        ll c = 0;
        for (int i = 1; i <= n; ++i) {
            c += (a[i] - down - k) * (a[i] - down - k);
        }
        res = min(c, res);
    }
    cout << res << endl;

    return 0;
}

C

水省

D

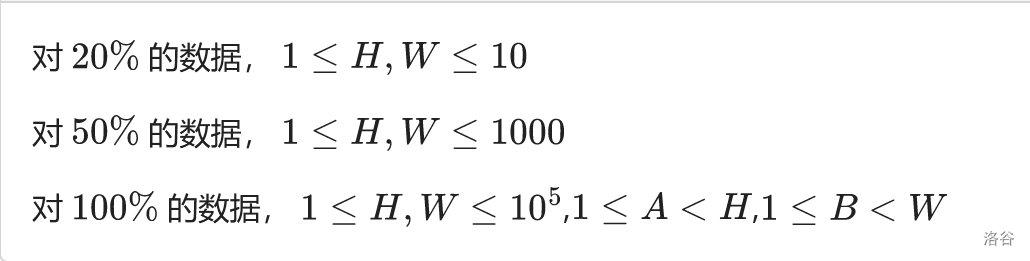
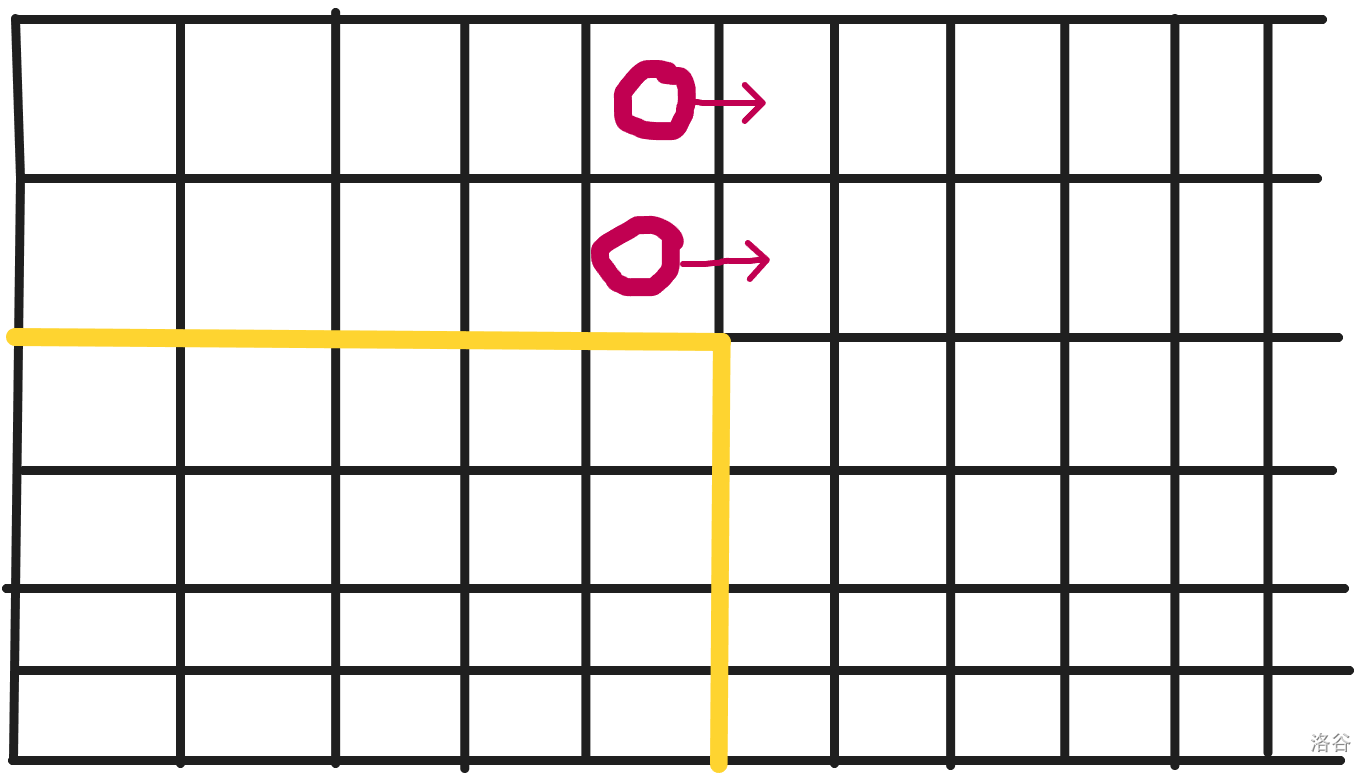
首先，我们明确一点，一个点从方格中向下走 \(i\) 步，向右走 \(j\) 步的方案是\(\tbinom{i}{j+i}\)

整个方案数打出来就是一副斜着的杨辉三角

那接下来就可以做了，我们算一下贴着右边的点，然后强制让他们向右走一步，再算出到终点的方案数，这样不会算重

#include <iostream>
#define ll long long
#define ull unsigned long long
#define ld long double

using namespace std;
const int mod = 1e9 + 7, maxN = 2e5 + 10;
ll h, w, a, b;
ll pre[maxN], inf[maxN];

inline ll ksc(ll x, ll y) {
    ll z = (ld)x / mod * y;
    ll res = (ull)x * y - (ull)z * mod;
    return (res + mod) % mod;
}

ll qmi(ll x, ll a) {
    ll ans = 1ll;
    while (a) {
        if (a & 1)
            ans = (x * ans) % mod;
        x = (x * x) % mod;
        a >>= 1;
    }
    return ans;
}

ll C(ll n, ll m) {
    if (n == 0 || m == 0)
        return 1ll;
    return (pre[n] * inf[n - m] % mod) * inf[m] % mod;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> h >> w >> a >> b;
    h--, w--, a--, b--;
    pre[0] = inf[0] = 1ll;
    for (ll i = 1; i <= h + w + 2; ++i) {
        pre[i] = (pre[i - 1] * i) % mod;
        inf[i] = qmi(pre[i], mod - 2);
    }
    ll ans = 0ll;
    for (int i = 0; i < h - a; ++i) {
        ll p = C(i + b, b), q = C(h - i + w - b - 1, h - i);
        ans = (ans + (p * q) % mod) % mod;
    }
    cout << ans << endl;

    return 0;
}

E

首先，这个不平衡的字符串是一个二元关系，只和出现次数最多的字符与其他字符有关

我们枚举这个字符，然后忽略无关因素，将枚举的字符记为 1 ，其他字符记为 -1 ，问题就转化为，对于一个区间 \([l,r]\) 求最大的 \(r-l+1\) 使得区间中 1 的个数大于 \(\left\lceil\frac{r-l+1}{2}\right\rceil\)

那这个东西明显可以用前缀和来优化，问题可以转化为对于位置 \(i\) ，求出最靠前的满足 \(pre[i]-pre[j]>0\) 的位置 \(j\)

这个明显可以直接树状数组，但是这里我们有线性的做法

我们发现，在树状数组的方法中，有一些计算是不必要的

比如说我们已经知道了在前 \(i\) 个前缀中没有小于 \(k\) 的，如果之后的位置的前缀和小于了 \(k\) 那答案一定不在上文的区间中

具体到做法来说，明显，随着枚举位置的增加，最长长度 mlen 不会减少，那我们维护一个前缀最大值，然后对于每一个位置，先判断在 \([1,i-len+1]\) 这个区间之内有没有符合要求的节点，如果有，那就不断地让 mlen++ ，如果没有，那一定对于答案没有贡献，过掉就可以了

#include <iostream>
#include <string>
#include <string.h>

using namespace std;
const int maxN = 1e6 + 10;
string str;
int pre[maxN], a[maxN], maxx[maxN], n;

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> str;
    n = str.length();
    int res = 0;
    for (int k = 0; k < 26; ++k) {
        for (int i = 1; i <= n; ++i)
            if (str[i - 1] - 'a' == k)
                a[i] = 1;
            else
                a[i] = -1;
        for (int i = 1; i <= n; ++i) pre[i] = pre[i - 1] + a[i], maxx[i] = min(maxx[i - 1], pre[i]);
        int len = 1;
        for (int i = 1; i <= n; ++i)
            while (pre[i] > maxx[i - len - 1] && i - len >= 1) ++len;
        res = max(len, res);
        for (int i = 1; i <= n; ++i) pre[i] = a[i] = 0, maxx[i] = 0x7ffffff;
    }
    if (res == 1)
        cout << "-1" << endl;
    else
        cout << res << endl;

    return 0;
}

F

带修序列最大独立集

DDP 板子题

我们容易写出矩阵，然后套线段树就可以了

这里是 \(max\,\,plus\) 矩阵

\[\begin{bmatrix} f_{i-1,0} &f_{i-1,1} \end{bmatrix} \times \begin{bmatrix} 0&a_i\\ 0&0 \end{bmatrix}= \begin{bmatrix} f_{i,0}&f_{i,1} \end{bmatrix} \]

但是有不用矩阵的做法，而且好像是 \(well-konwn\) 的

这里贴一下zmy的题解

lxl 也会这个

这个做法的妙点在其合并区间的时候将端点进行了分类排除，使其可以合并

第二种做法的代码没写，只有第一种的

#include <iostream>
#define ll long long
#include <string.h>

using namespace std;
const int maxN = 5 * 1e4 + 10;
int son[maxN * 2][2], a[maxN], n, m, idx = 1;

struct matrix {
    ll g[2][2];
    matrix() { memset(g, -0x3f, sizeof(g)); }
    matrix operator*(matrix b) {
        matrix c;
        for (int i = 0; i < 2; ++i)
            for (int j = 0; j < 2; ++j)
                for (int k = 0; k < 2; ++k) c.g[i][j] = max(c.g[i][j], g[i][k] + b.g[k][j]);
        return c;
    }
} data[maxN * 2];

void build(int now, int l, int r) {
    if (l == r) {
        data[now].g[0][1] = a[l];
        data[now].g[1][0] = data[now].g[0][0] = 0;
        return;
    }
    int mid = (l + r) >> 1;
    son[now][0] = ++idx;
    build(idx, l, mid);
    son[now][1] = ++idx;
    build(idx, mid + 1, r);
    data[now] = data[son[now][0]] * data[son[now][1]];
}

matrix query(int now, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr)
        return data[now];
    int mid = (l + r) >> 1;
    if (qr <= mid)
        return query(son[now][0], l, mid, ql, qr);
    else if (ql > mid)
        return query(son[now][1], mid + 1, r, ql, qr);
    else
        return query(son[now][0], l, mid, ql, qr) * query(son[now][1], mid + 1, r, ql, qr);
}

void modify(int now, int l, int r, int x) {
    if (l == r) {
        data[now].g[0][1] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    if (x <= mid)
        modify(son[now][0], l, mid, x);
    else
        modify(son[now][1], mid + 1, r, x);
    data[now] = data[son[now][0]] * data[son[now][1]];
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    build(1, 1, n);
    ll ans = 0;
    // cout << max(data[1].g[1][0],max(data[1].g[0][1],data[1].g[0][0])) << endl;
    while (m--) {
        int pos, x;
        cin >> pos >> x;
        a[pos] = x;
        modify(1, 1, n, pos);
        ans += max(data[1].g[1][0], max(data[1].g[0][1], data[1].g[0][0]));
    }
    cout << ans << endl;

    return 0;
}

G

• 若 \(a=\{a_1,a_2,\cdots a_n\}\) 存在 \(1\le x<y<z<w\le n+1\) 满足 \(\sum\limits_{i=x}^{y-1}a_i=X,\sum\limits_{i=y}^{z-1}a_i=Y,\sum\limits_{i=z}^{w-1}a_i=Z\) 时，则称数列 \(a\) 是好的。
• 求在所有长度为 \(n\) 且 \(a_i\in\mathbb{N}^{+}\cap[1,10]\) 的 \(10^n\) 个序列 \(a\) 中，有多少个序列是好的，答案对 \(10^9+7\) 取模。
• \(3\le n\le40\)，\(1\le X\le5\)，\(1\le Y\le7\)，\(1\le Z\le5\)。

编程兔有没有母亲啊，敢把这种东西放到山东普及补测来

首先第一反应拆分数，然后我rush 了一下发现过不了样例，因为这样一定会出现重复的问题，一个序列可能有多次匹配

那接下来根据数据范围来猜算法了，不是搜索就是状压

我们对于一个串被多次统计的问题，第一个想法就是找出一个代表的来统计，但是我们发现这是非常困难的，因为我们

这里我们统计不符合要求的串

怎么统计呢，我们有一个废话的结论，我们枚举字符串的结束，对于一个有俳句的串，其一定有一个后缀符合要求

如果直接枚举，判定很容易，但我们如果想一次统计多个串是否符合要求，那就需要进行分类

我们发现，在上一个DP中，算重的原因是一个状态在判定为合法后会继续计算，我们如果想去掉这个问题只可能上容斥，但这个容斥过于不伦不类，无法实现，所以我们想到了状压

我们先考虑对整个数组进行状压，考虑怎么把不是二进制的数压到二进制

我们这么考虑，对于一个数 \(i\)，就把原来的状态左移 \(i\) 位，然后再填上一个 1 就可以了，初始状态设为 1

这样我们就可以判了，对于 \(X,Y,Z\) 也这样构造出一个这样的串，称为基本串，同时对于每个串的每一个后缀，看一看两个与起来是不是还是基本串

好的，这里的状压已经可以保证不重不漏了，接下来是优化复杂度

假设我们枚举到了第 \(i\) 位，那明显，每个状态只有最后的 \(X+Y+Z+1\) 是有效的

所以我们直接舍弃超出范围的位就可以了，这里的操作其实就是将一整个状态归入其末尾的状态

这个题提醒了我们，状压是可以压正数的，同时状压的状态可以简化，可以归纳

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define ld long double
#define inf 0x7ffffff
#define int ll

using namespace std;
const int mod=1e9+7;
int n,x,y,z;
int ed,f[50][(1<<17)+10];
int tot,ans;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	cin >> n >> x >> y >> z;
	f[0][0]=1;
	tot=(1<<(x+y+z))-1;
	ed|=1<<(x-1);
	ed=((ed<<(y))|(1<<(y-1)));
	ed=((ed<<(z))|(1<<(z-1)));
	ans=1;
	for(int i=1;i<=n;++i){
		ans=(ans*10)%mod;
		for(int j=0;j<=tot;++j){
			if(f[i-1][j]==0) continue ;
			for(int k=1;k<=10;++k){
				int s=((j<<k)|(1<<(k-1)));
				s&=tot;
				if((s&ed)!=ed) {
					f[i][s]=(f[i][s]+f[i-1][j])%mod;
				}
			}
		}
	}
	for(int i=0;i<=tot;++i)
		ans=(ans-f[n][i]+mod)%mod;
	cout << ans<<endl;
	
	return 0;
} 

H

我没写，暂时不补