构造题选练

目录

• 前言
• 抽屉原理
  • 基本思想
  • 例题
    • CF1534D
    • 分析
    • CF1198C
    • 分析
    • CF1450C2
    • 分析
• DFS树
  • • CF1364D
    • 分析
    • CF1391E
    • 分析
• 归纳法
  • • CF1470D
    • 分析
    • CF1515F
    • 分析
• 图上转化
• 二进制问题
• 随机化

前言

作者非常的菜，很多的交互也是看了题解才学会的，请各位dalao体谅
另外我也希望各位dalao能给我推荐一些好的 交互 / 构造 题，蒟蒻不甚感激

抽屉原理

基本思想

抽屉原理最经典的运用就是存在性问题以及对问题进行一定的分组

存在性问题的代表题目就是大名鼎鼎的量子通信

在交互题中，我们可能经常遇见如交互次数为 \(\dfrac{n}{k}\) 的问题，这个时候就可以考虑抽屉原理

一般来说，抽屉原理的难点在于如何将状态进行划分，我们要求不同的状态能够相互推出，或者相互独立能满足题目要求

做这种题的一般解法：

1. 根据交互次数 / 题目要求猜出 有用/无用 状态数
2. 思考如何将问题划分为不同的部分，以及如何控制不属于这两个部分的状态的数量
3. 进行划分

一般来说，划分的方法应该将不同的类别联系起来，才能有较好的效果

另外，不要试图在所有的形如 \(\dfrac{n}{k}\) 的题中尝试抽屉原理，会死的很惨

例题

CF1534D

你有一棵 \(n\) 个节点的树，树上每条边长度为 \(1\)，但你不知道这棵树的结构。

你可以对系统进行不超过 \(\lceil \frac{n}{2} \rceil\) 次的询问，每次可以询问一个满足 \(1 \le x \le n\) 的节点 \(x\)。

对于询问的 \(x\)，系统会给你 \(n\) 个数，第 \(i\) 个数代表节点 \(i\) 与节点 \(x\) 的简单路径长度。

请你还原出这棵树的结构。

$ 2 \le n \le 2,000 $

分析

这道题是一道十分经典的题

我们观察交互次数，要求我们至少将总状态划分为两个以上可以互推的状态

对于一次询问而言，路径长度大于 1 的点我们无法确定其具体的位置，但对于路径为 1 的点，我们可以确定其一定相连，这就意味着相邻的节点可以互推

我们指定一个节点为根，进行一次询问，得到所有点的dep，再dep的奇偶进行分类，由于相邻节点dep差为 1 ，可以得到整棵树的结构

可以证明询问次数严格小于等于题目要求

#include <iostream>
#include <vector>

using namespace std;
const int maxN=2010;
int n;
vector<int> g[maxN];
int col[maxN],len[maxN],temp[maxN];
int sum1=0,sum2=0;
int vis[maxN];

void dfs(int now){
	for(int x:g[now]){
		if(!vis[x]){
			cout << now << " " << x << endl;
			vis[x]=1;
			dfs(x);
		}
	}
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	cin >> n;
	cout << "? " << 1 << endl;
	col[1]=-1;
	for(int i=1;i<=n;++i) {
		cin >> len[i];
		if(len[i]==1){
			g[1].push_back(i);
			g[i].push_back(1);
		}
		if(len[i]&1) sum1++,col[i]=1;
		else if(len[i]!=0) sum2++,col[i]=0;
	}
	int sy=1;
	if(sum1>sum2) sy=0;
	for(int i=1;i<=n;++i)
		if(col[i]==sy){
			cout << "? " << i << endl;
			for(int j=1;j<=n;++j){
				int x;
				cin >> x;
				if(x==1)
					g[j].push_back(i),g[i].push_back(j);
			}
        }
	vis[1]=1;
	cout << "!" << endl; 
	dfs(1);
	return 0;
} 

CF1198C

给一个无向图，\(3\times n\) 个点， \(m\) 条边，请找大小为 \(n\) 的点独立集或边独立集。

分析

题目给定的要求，我们可以将总状态化为三份，但其实我们观察条件，给出的答案只有两个类型

意味着最好将问题化为两种，留下一部分的无用状态

发现一个特性，如果我们将整个图中找出一个尽可能大的边独立集，我们会发现，其余的不在边独立集两边的点就构成了一个点独立集

证明显然，如果两个点之间有一条边，因为我们已经确定在原图中不能再有边加入这个边独立集了，所以这条边的顶点一定与已经入独立集的点相连，这与我们的假设矛盾，所以得证

我们分析一下，如果边独立集的边数小于 \(n\) ，那被划入点独立集的点一定大于等于 \(n\) 。反之，边独立集就符合了要求

我们这样做，枚举每一条边，若两顶点都不是已入独立集边的顶点就加入，将两顶点标记

#include <iostream>
#include <vector> 

using namespace std;

const int maxN=5*1e5+10;
struct node {
	int from,to;
}g[maxN];
vector<int> edge[maxN],ans;
int vis[maxN],have[maxN];

void solve(){
	int n,m;
	cin >> n >> m;
	for(int i=1;i<=m;++i){
		have[i]=0;
		cin >> g[i].from >> g[i].to;
		edge[g[i].from].push_back(i);
		edge[g[i].to].push_back(i);
	}
	for(int i=1;i<=n*3;++i) vis[i]=0;
	int sum=0;
	for(int i=1;i<=m;++i){
		if(have[i]) continue ;
		if(!vis[g[i].from]&&!vis[g[i].to]){
			ans.push_back(i);
			++sum;
			vis[g[i].to]=vis[g[i].from]=1;
			for(int x:edge[g[i].to]) have[x]=1;
			for(int x:edge[g[i].from]) have[x]=1;
		}
	}
	if(sum>=n){
		cout <<  "Matching" <<endl;
		for(int i=0;i<n;++i){
			cout << ans[i] << " ";
		} 
		cout << endl;
	}
	else {
		cout << "IndSet" << endl;
		int k=0;
		for(int i=1;i<=n*3;++i){
			if(!vis[i]){
				cout << i << " ";
				++k;
			} 
			if(k==n) break;
		} 
		cout << endl;
	}
	ans.clear();
	for(int i=1;i<=n*3;++i) edge[i].clear();
	
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	int t;
	cin >> t;
	while(t--){
		solve();
	}
	
	return 0;
} 

CF1450C2

给定一张 \(n\) 行 \(n\) 列的棋盘，每个格子可能是空的或包含一个标志，标志有 \(\text{X}\) 和 \(\text{O}\) 两种。

如果有三个相同的标志排列在一行或一列上的三个连续的位置，则称这个棋盘是一个 胜局，
否则称其为 平局。

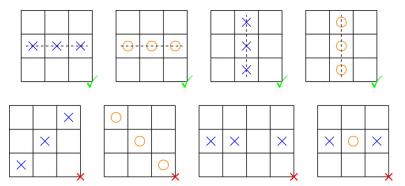
例如，上图第一行的局面都是胜局，而第二行的局面都是平局。

在一次操作中，你可以将一个 \(\text X\) 改成 \(\text O\)，或将一个 \(\text O\) 改成 \(\text X\)。

设棋盘中标志的总数为 \(k\)，你需要用不超过 \(\lfloor \frac{k}{3}\rfloor\)
次操作把给定的局面变成平局。

\(1\leq n\leq 300\)。

分析

大的来了

这道题十分的 Hard ，但也十分有启发性

首先，我看完题有一个基本的想法，就是如果我们对每一个三连调整一个位置，是不是就可以了

但你会发现这是假的，因为调整过后的位置有可能会影响其他的位置

这就是状态之间没有独立性

我们想要使状态之间有独立性，那就要站在整体的角度进行分析，怎么去构造这个图，使得调整不会影响到其他的位置

三个相邻的格子，其横纵坐标之和一定构成了一个\(\pmod 3\)的剩余系，所以我们最终的状态只要保证其所有的三个连着的不连续就行了

考虑状态的划分，我们可以将三个不连续的中的两个位置改反

具体的说，我们将图进行分层，分完后长这样（图来自题解）

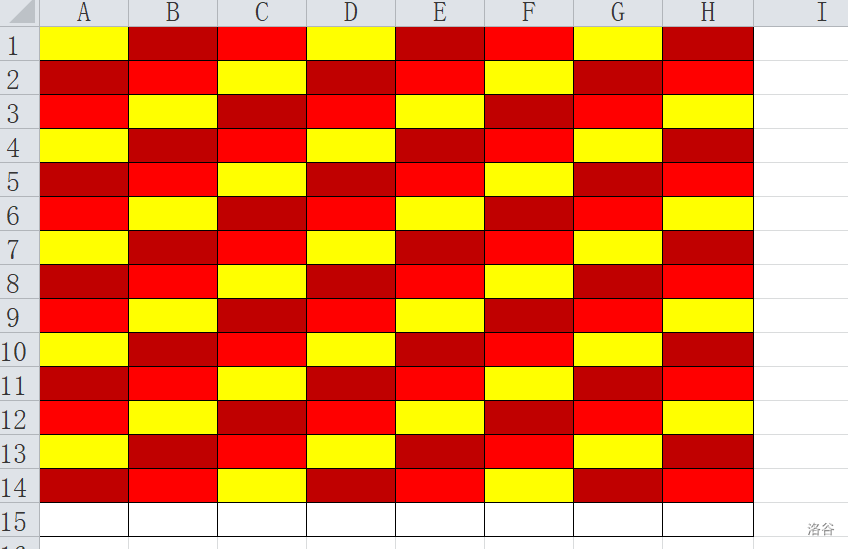
我们有三种构造方案：

1. 将黄色的都该成 O ,红的都改成 X
2. 将红的都改成 O , 浅红的都改成 X
3. 将浅红的改为 O , 黄的都改为 X

你会发现，这三种操作所涉及的点都是相互独立的，不会有相互影响

直接染色，枚举即可

#include <iostream>
#include <vector> 
#include <string>
#include <string.h>

using namespace std;
const int maxN=400;
int dx[5]={0,0,1,-1},
	dy[5]={1,-1,0,0};
int n;

inline int onmap(int x,int y){
	return x>=0&&x<=n&&y>=0&&y<=n; 
}

void solve(){
	string str[maxN];
	int a[maxN][maxN],w[maxN][maxN],col[maxN][maxN];
	cin >> n;
	for(int i=1;i<=n;++i)
		cin >> str[i];
	for(int i=1;i<=n;++i){
		for(int j=0;j<n;++j){
			w[i][j+1]=0,col[i][j+1]=0;
			if(str[i][j]=='O') a[i][j+1]=1;
			if(str[i][j]=='X') a[i][j+1]=2;
			if(str[i][j]=='.') a[i][j+1]=0;
		}
	}
	for(int i=1;i<=n;++i)
		for(int j=1;j<=n;++j)
			col[i][j]=(i+j)%3+1;
	int p1,p2,ans,sum=0x7ffffff;
	p1=1,p2=2;
	int temp=0;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(col[i][j]==p1&&a[i][j]==1)
				++temp;	
			if(col[i][j]==p2&&a[i][j]==2)
				++temp;
		}
	}
	if(temp<sum) ans=1,sum=temp;
	p1=2,p2=3,temp=0;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(col[i][j]==p1&&a[i][j]==1)
				++temp;	
			if(col[i][j]==p2&&a[i][j]==2)
				++temp;
		}
	}
	if(temp<sum) ans=2,sum=temp;
	p1=3,p2=1,temp=0;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(col[i][j]==p1&&a[i][j]==1)
				++temp;	
			if(col[i][j]==p2&&a[i][j]==2)
				++temp;
		}
	}
	if(temp<sum) ans=3,sum=temp;
	if(ans==3) p1=3,p2=1;
	if(ans==2) p1=2,p2=3;
	if(ans==1) p1=1,p2=2;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			if(!a[i][j]) cout << ".";
			else if(col[i][j]==p1&&a[i][j]==1) 
				cout << 'X';
			else if(col[i][j]==p2&&a[i][j]==2)
				cout << 'O';	
			else cout << str[i][j-1] ;	
		}
		cout << endl;
	}	
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	int t;
	cin >> t;
	while(t--){
		solve();
	}
	return 0;
} 

DFS树

DFS 树是解决图上边直接相连的一个重要方法，我们这里分为三种图进行举例

解释一下名词：
非树边：不属于树边的边
横叉边：由一个节点连向非祖先节点的非树边
返祖边：一个节点连向其祖先节点的非树边

1. 无向图
   无向图中，DFS树的特点是没有横叉边，即一个点只有可能与其子树内或者祖先节点相连
2. DAG
   在一个DAG中，DFS树没有返祖边，意味着一个点不可能与其祖先节点有直接连边
3. 仙人掌
   由于仙人掌中的每一条边都在最多一个环里，我们DFS树的返祖边会正好覆盖仙人掌的一条链，这条链和这个边就构成了一个简单环

我们在图上连边问题中经常会用到DFS树来解决问题

另外，当整个图是一棵树的时候，有一些 DFS 树上的性质会消失，需要特殊考虑

CF1364D

给出一张 \(n\) 个点的无向连通图和一个常数 \(k\)。

你需要解决以下两个问题的任何一个：

1. 找出一个大小为 \(\lceil\frac k2\rceil\) 的独立集。
2. 找出一个大小不超过 \(k\) 的环。

独立集是一个点的集合，满足其中任意两点之间在原图上没有边直接相连。

可以证明这两个问题必然有一个可以被解决。

$ 3 \le k \le n \le 10^5 $ , $ n-1 \le m \le 2 \cdot 10^5 $

分析

这道题是一个典型的 DFS 树类问题，我们一旦看到了形如“独立集”“最多有多少条边相连”“环”之类的构造，就要想起DFS树

我们对于DFS树上的每一个节点，都维护一个其能通过非树边到达的深度最小的节点 \(low_i\)

我们发现，每一个 \(low_i\) 对应着一个环，如果这个环小于k，直接输出就行了

如果其环的长度大于k，那我们隔一个选一个，就没有问题了，因为我们这里处理的是最小的环，我们可以确定在 \(i\) 和 \(low_i\)之间没有在这个区间内的返祖边了

树的情况需要特判

#include <iostream>
#include <vector>
#define inf 0x7ffffff

using namespace std;
const int maxN=2*1e5+10;
vector<int> g[maxN];
int n,m,k,dep[maxN],low[maxN],fa[maxN];

void dfs(int now,int f){
	dep[now]=dep[f]+1,low[now]=0x7ffffff,fa[now]=f;
	for(int x:g[now]){
		if(x==f) continue ;
		if(dep[x]){
			if(dep[x]<dep[now])
				low[now]=min(low[now],abs(dep[now]-dep[x])+1);
		}
		else dfs(x,now);
	}
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	cin >> n >> m >> k;
	for(int i=1;i<=m;++i){
		int u,v;
		cin >> u >> v;
		g[u].push_back(v),g[v].push_back(u);
	}
	dfs(1,1);
	for(int i=1;i<=n;++i){
		if(low[i]<=k){
			cout << 2 << endl;
			cout << low[i] << endl;
			int p=i;
			while(low[i]--){
				cout << p << " ";
				p=fa[p];
			}
			cout << endl;
			return 0;
		}
	}
	int e=(k&1)?(k+1)/2:k/2;
	cout << 1 << endl;
	for(int i=1;i<=n;++i){
		if(low[i]!=inf){
			int q=(k%2)?(k+1)/2:k/2,p=i;
			while(e--){
				cout << p << " ";
				p=fa[p],p=fa[p];
			}
			cout << endl;
			return 0;
		}
	}
	vector<int> t[3];
	for(int i=1;i<=n;++i)
		t[(dep[i]&1)+1].push_back(i);
	if(t[1].size()>t[2].size()) {
		for(int i=0;i<e;++i) cout << t[1][i] << " ";
		cout << endl;
	}
	else {
		for(int i=0;i<e;++i) cout << t[2][i] << " ";
		cout << endl;
	}
	return 0;
} 

CF1391E

给出一张无向连通图，选择以下任意一个任务完成：

• 找到图中一条至少包含 \(\lceil \frac {n} {2} \rceil\) 个点的简单路径。
• 找到图中偶数（至少 \(\lceil \frac {n} {2} \rceil\) ）个点，且将它们两两配对。使满足任意两个点对包含的 \(4\) 个点的导出子图至多存在 \(2\) 条边。

其中，简单路径指不重复经过任意一个点的路径；导出子图指由给定点集与原图中两顶点均在给定点集中的边构成的图。

若完成任务 \(1\)，则输出 PATH，并输出简单路径包含的点数与该路径依次经过的点。

若完成任务 \(2\)，则输出 PAIRING，并输出选出的点对数及每一组点对。

$ n, m $ ( $ 2 \le n \le 5\cdot 10^5 $ , $ 1 \le m \le 10^6 $ )

分析

其实我觉得这道题和上一道题差不多难度，不该评个紫

在无向图中，不同子树的点之间不会存在非树边，所以我们直接构建出来 DFS 树，再判断

1. 如果树高高于\(\lceil \frac {n} {2} \rceil\)，就直接输出路径
2. 反之，我们每一层的节点相互匹配，因为树高小于\(\lceil \frac {n} {2} \rceil\)，我们每一层撑死只有一个点无法被匹配，所以总匹配数一定大于\(\lceil \frac {n} {2} \rceil\)

要真说这题闭上一题有哪些难点吧，就是最后的抽屉原理比较难想吧

#include <iostream>
#include <vector> 
#define pii pair<int,int>

using namespace std;
const int maxN=5*1e5+10;
int n,m,t,dep[maxN],fa[maxN];
vector<int> g[maxN],cnt[maxN];
vector<pii> ans;
int maxd;

void dfs(int now,int f){
	dep[now]=dep[f]+1,cnt[dep[now]].push_back(now),fa[now]=f;
	for(int x:g[now]) if(!dep[x]) dfs(x,now);
}

void print(int now){
	if(fa[now]) print(fa[now]);
	cout << now << " ";
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	cin >> t;
	while(t--){
		cin >> n >> m;
		int k=(n%2)?((n+1)/2):(n/2);
		for(int i=0;i<=n;++i) g[i].clear(),dep[i]=0,fa[i]=0;
		int u,v;
		for(int i=1;i<=m;++i)
			cin >> u >> v,g[u].push_back(v),g[v].push_back(u);
		dfs(1,0);
		int maxx=0,id=0;
		for(int i=1;i<=n;++i)
			if(dep[i]>maxx) maxx=dep[i],id=i;
		if(maxx>=k){
			cout << "PATH"<< endl << maxx << endl;
			print(id);cout << endl;
			for(int i=1;i<=maxx;++i) cnt[i].clear();
			continue; 
		}
		cout << "PAIRING" << endl;
		int sum=0;
		for(int i=1;i<=maxx;++i){
			for(int j=0;j<cnt[i].size();j+=2)
				if(j+1<cnt[i].size()) ans.push_back({cnt[i][j],cnt[i][j+1]}),++sum;
			cnt[i].clear();
		}
		cout << sum << endl;
		for(pii x:ans) cout << x.first << ' ' << x.second << endl;
		ans.clear();
	}
	
	
	return 0;
}

归纳法

归纳法在OI中一直有这重要的应用，很多交互结论的的证明都依赖于归纳法

一般来说，我们利用归纳法来解决一系列的问题

反正这个东西不结合题来说根本不可能，而且很多题都非常的ad-hoc

CF1470D

给定一个 \(n\) 个节点，\(m\) 条无向边的图，现在你要给一些点染色，使得：

• 一条边所连接的两个点不能都被染色。
• 在所有连接两个不被染色的点的边都被删除的情况下，这个图满足任意两个点互相可达。

如果有染色方案满足上述要求，输出一行 YES 之后输出要染色的点的数量，并以任意顺序输出所有被染色的点的编号;否则输出一行 NO。

\(T\) 组询问。

$ 2 \le n \le 3 \cdot 10^5 $ , $ 0 \le m \le 3 \cdot10^5 $

分析

数学归纳

我们想一想，发现假设前\(n-1\)个节点都已经满足要求了，我们这个时候加入第\(n\)个节点

如果第\(n\)个节点与其他染色的点有边，那就不用染色了，如果没有，那就染上色

正确性显然

#include <iostream>
#include <vector> 

using namespace std;
const int maxN=3*1e5+10;
vector<int> g[maxN];
int vis[maxN],col[maxN];
void dfs(int now){
	if(col[now]==-1){
		col[now]=1;
		for(int x:g[now])col[x]=0;
	}
	for(int x:g[now])
		if(!vis[x]) {
			vis[x]=1;
			dfs(x);
		}
}

void solve(){
	int n,m;
	cin >> n >> m;
	for(int i=1;i<=n;++i) vis[i]=0,col[i]=-1,g[i].clear();
	for(int i=1;i<=m;++i) {
		int u,v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	vis[1]=1;
	dfs(1);
	int sum=0;
	for(int i=1;i<=n;++i){
		if(!vis[i]){
			cout << "NO" << endl;
			return ;
		}
		if(col[i]) ++sum;
	}
	cout << "YES" << endl << sum << endl;
	for(int i=1;i<=n;++i) {
		if(col[i]) cout << i << " ";
	} 
	cout << endl;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	int t;
	cin >> t;
	while(t--){
		solve();
	}

	return 0;
} 

CF1515F

给定一张 \(n\) 个点 \(m\) 条边的无向连通图和正整数 \(x\)，点有非负权值 \(a_i\)。

如果一条边 \((u,v)\) 满足 \(a_u+a_v \ge x\)，可以将 \(u,v\) 缩起来，新点的点权为 \(a_u+a_v-x\)。

判断这张图是否可以缩成一个点。如果是，还要输出每次缩的是哪条边。

\(2 \le n \le 3 \cdot 10^5,n - 1 \le m \le 3 \cdot 10^5,1 \le x \le 10^9,0 \le a_i \le 10^9\)

分析

这里你将感受到数学归纳的力量

我们设计一个数学归纳的时候，一定要想一想我们怎么加入新的状态，同时以什么为标准进行归纳

明显，我们这种折叠边的操作最后会形成一棵树，所以我们对树上的节点进行归纳

随便来一颗生成树，明显当总权值不能满足总折叠的费用的时候无解，反之，则有解，我们称第二种状态为满足状态

开始归纳证明，对于每一个叶节点，我们定义其为我们的临近状态进行讨论，我们假定对于规模为\(n-1\)的状态一定有解，设新加入节点为\(i\)

1. \(a_i+a_{fa_i}\geq x\)，这时我们直接折叠，就转化为了规模-1的问题
2. \(a_i+a_{fa_i}\leq x\)，这个时候，我们将这个节点放在后面再做，因为我们的假设，规模为\(n-1\)的满足状态是有解的，而 \(a_i+a_{fa_i}\leq x\)，则其父亲所在的不包含 \(i\) 的联通块一定是一个满足状态，因此我们就从其父亲处进行折叠，最后剩下的一定可以再和 \(i\) 折叠

具体实现，拿个栈，是第二种情况就往里面压，是第一种情况就直接正序记录一下

这个代码写的很丑，不建议学习

#include <iostream>
#include <vector> 
#define pii pair<int,int>
#define int long long 

using namespace std;
const int maxN=6*1e5+10;
int a[maxN],n,m,x,vis[maxN],cnt1=0,cnt2,fa[maxN];
vector<pii> g[maxN];
int ans[maxN];
int f[maxN];

void dfs(int now,int f,int fm){
	vis[now]=1,fa[now]=f;
	for(pii x:g[now]){
		if(vis[x.first]) continue;
		dfs(x.first,now,x.second);
	}
	if(now==1) return ;
	if(a[now]>=x)
		ans[++cnt1]=fm,a[f]=a[f]+a[now]-x;
	else ans[--cnt2]=fm;
}

int acc(int x){
	if(f[x]==x) return x;
	return f[x]=x;
}

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0); 
	cin >> n >> m >> x;
	int sum=0;
	cnt2=n;
	for(int i=1;i<=n;++i) cin >> a[i],sum+=a[i],f[i]=i;
	for(int i=1;i<=m;++i){
		int u,v;
		cin >> u >> v;
		if(acc(u)==acc(v)) continue; ;
		f[acc(u)]=acc(v);
		g[u].push_back({v,i});
		g[v].push_back({u,i});
	}
	if((n-1)*x>sum) {
		cout << "NO" << endl;
		return 0;
	}
	dfs(1,0,0);
	for(int i=1;i<=n;++i){
		if(!vis[i]){
			cout << "NO" << endl;
			return 0;
		}
	}
	cout << "YES" << endl;
	for(int i=1;i<n;++i) 
		cout << ans[i] << endl;
	cout << endl;
	return 0;
} 

图上转化

二进制问题

随机化