阶乘的末尾0数及最后的非0数字的快速解法

求 𝑛! 十进制表示下末尾 0 的个数与最后一位非 0 位权值。

我 Bing 了好久，出来的都是些神仙做法

讲一下 Luogu 课上 RSY 老师的做法吧

Q1

题意等价于，求 \(V_{10}(n!)\)

\(V_{k}(n)\) 等于最大的 \(p\) ，使得 \(p^k \mid n\)

这里需要用到一个公式，在下面给出 ：

勒让德定理:

\[V_p(n!)=\sum_{k\geq 1}\left\lfloor\dfrac{n}{p^k}\right\rfloor\,\,\,\,\,\,\,\, p为素数 \]

百度百科害人不浅，把下取整打成中括号，害我看了好久

其本质就是一个算两次原理的运用，\(p^K\) 会贡献 \(k\) 的大小，分别在 \(1-k\) 的时候每次贡献 \(1\)，后面的柿子相当于求 \(p^k\) 在\(1-n\)中整除多少个数，关于为什么要求 \(p\) 为素数，我也没想明白

总之，我们发现，10 = 5 * 2，同时 5 的倍数的个数一定小于 2 的倍数，所以我们统计 \(V_5{n!}\) 就可以了，复杂度 \(O(log_5n)\)

Q2

这一问就比上一问难多了，我们相当于要求\(\dfrac{n!}{10^{V_5(n)}} \pmod{10}\)

\(V_5(n!)\)可以通过上一问求出来，现在看看接下来怎么做

我们可以考虑使用 CRT ,将模数拆成 2 和 5 两个质数，相当于我们构造了两个方程，\(x \equiv k_1 \pmod{2}\) 和 \(x \equiv k_2 \pmod{5}\)，这里的 \(k_1,k_2\) 都是可以直接求出来的，而\(x\) 一直是 \(\dfrac{n!}{10^{V_5(n)}}\)，利用 CRT 可以 拼出来在 \(\pmod{10}\) 之下的结果

感谢 rsy 的答疑解惑 气场太强直接逼我想出来了

那我们先考虑 \(\pmod {2}\) 下的结果

很显然，若 \(n\geq 2\) 那答案就是 0 ，反之则是 1

对于 \(\pmod{5}\)，我们发现，分母上除的效果就是删去了所有的 5 的倍数，举个例子

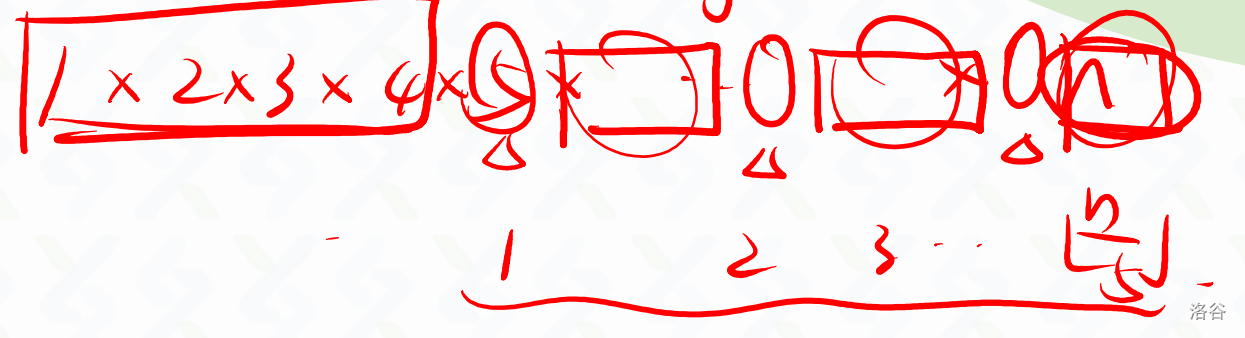
来自讲课课件

我们去掉了一遍 5 的倍数，相当于从数列中把所有 5 的倍数先除以 5 ，可以看到，数列被分成了不同的区间，每一个区间在 \(\pmod{5}\) 意义下都是 1 2 3 4 ，对于序列中 5 的倍数，我们发现其在除以 5 之后 变成了 1 2 3 4 ……，因此可以递归下去，继续解决

复杂度 \(O(log_5 n)\)

目前没有代码