网络流32题

%%% wql dalao

题目来自浅谈网络流的各种建模方法

作为 wql dalao 的一点补充说明，不会太学术（蒟蒻也不会证明

同时，在写完了所有题目之后，有可能加入一些章节

所有最大流算法均采用加了优化的 Dinic ，费用流为 Dinic+spfa

多源多汇建模

一般图多源多汇建模

P1402 酒店之王

三分图匹配，不同于二分图匹配，我们要防止中间的点被选两次，因此要拆点

代码

P2756 飞行员配对方案问题

一眼丁真鉴定为，二分图匹配

正常的套路了，对于一个二分图，建出源汇，跑 Dinic

代码

二分图最小顶点集覆盖 Kőnig 定理

二分图最小顶点覆盖与二分图最大匹配相等

最小顶点覆盖指的是我们在二分图中选出一些点，使得所有的边的两个端点中至少有一个在我们选的点之中

证明略，可以去看原文（反正我看不懂

顶点覆盖可以帮我们解决一些对于一个东西，有两个维度，我们只要在至少一个维度上选了它，就可以了之类的问题

最经典的应用就是网格图上的问题

UVA11419 SAM I AM

请使用 c++ 11提交此题，不然会 UKE

我们把行视为二分图的右部端点，列视为左边的

每有一个关键点出现，我们就把它所在的行和列连起来，问题就转化为了一个最小顶点覆盖问题

跑 Dinic ,接下来的问题就是如何输出方案

我们以行的角度来思考，跑完了 Dinic 之后，肯定有一些边已经满流了，整个图也被划分为了两部分

如果一条连接二分图两边的边满流了，我们就视为其选了这一行

对于列来说，我们只要输出有点，但对应的行没有选的列就行了

具体到做法上，我们进行一次搜索，不跑满流的边，对于左边的点，若是不能被搜到，则其在割里面，我们要将其输出

对于右边的点，其若能被搜到，则与其相连的左边的点中有没有选的（不在割里），我们要将其选上

更具体的看代码

代码

二分图最大独立集

二分图最大独立集 = 总点数 - 二分图最小点覆盖

至于为什么，我不会证，也不想证，具体去看原文吧

并没有题

最大流最小割定理

很经典，原文的证明十分严谨，这里帮大家感性理解一下

首先，最小割是肯定不能小于最大流的，如果最小割小于了最大流，就代表其一定有一个更小的流存在，这与最大流矛盾

其次，最小割是不能大于最大流的，如果大于，其一定割了一些根本就没有水流过的边，或者其没有割在增广路的瓶颈上

所以，最小割等于最大流

如果想看严谨证明还是去原文吧，但是没有人话

拆点法

如果我们想要限制一个点能经过的流量，就将其拆成两个点，在中间连一条大小为限制容量的边

另一种情况是一个点包含多个状态，则我们需要把不同的状态拆开，然后再继续

下面的例子分别对应了两种情况

P1345 奶牛的电信

一般来说，对于这一类题，删点是十分困难的，所以我们进行拆点，转化为删边

把 u 拆成 u' 和 u'' ，中间连一条容量为 1 的边就行了

同时注意，这道题是要连双向边的

对于 wql 留的思考题，其实第一条是因为写法不同，如果你是把 s 设成了输入起点的入边，则自然要连 inf 的边，如果你之间从出边开始跑，那连不连 inf 就无所谓了

对于第二问，十分显而易见，代码里是连的 inf

代码

P2053 [SCOI2007] 修车

挺难的一道题，我们这里会主要介绍网络流的转化和其方案的正确性

首先，明确一下题意，在同一时刻，不允许有一个工人修多辆车，一辆车被多个工人修，但可以多辆车被多个人修

人不能两次踏进同一条河流，因为第二次踏进时河流已经变了

对于这道题，我们只要最小化所有人等的时间的和就可以了，可能最朴素的想法就是每一辆车和工人做匹配，但我们发现，这种思路是有后效性的，我们直接跑匹配，会使得一个工人修的不同车的主人拿到车的先后顺序无法确认

所以我们想到，增加状态，弥补问题

对于一辆车，我们认为钦定其是哪位工人修的第几辆车，具体的，我们把 \(m\) 个工人拆成 \(n*m\) 个点，\((i,k)\)点代表第 \(i\) 位工人修的倒数第 \(k\) 辆车，那我们对每辆车流流量时，如下图

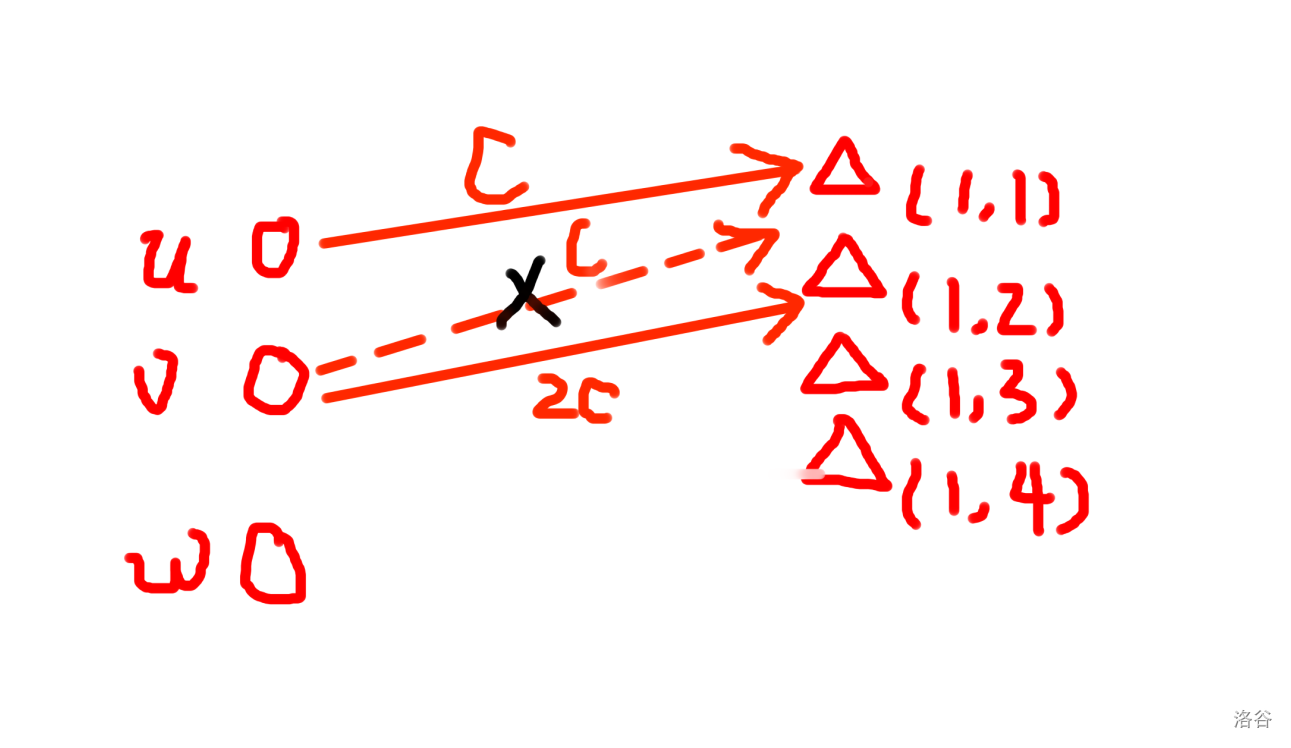
\(u\) 一开始匹配上了 \((1,1)\)，因为其边权小，后来轮到 \(v\) 来匹配，也想匹配上 \((1,1)\) ,但是人家名花有主了，匹配不上，就只能去选能选的边权最小的\((1,2)\)了

现在 MCMF 跑完了，对于一个师傅拆的点，我们就反着拿出来，如下图，边权越小，越后修

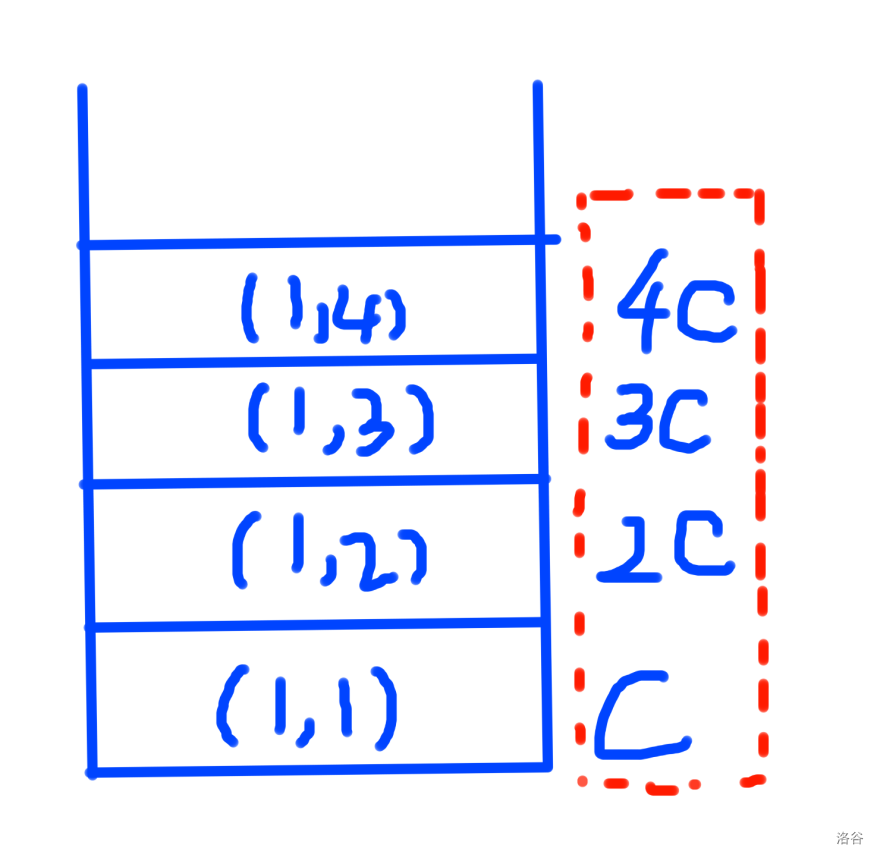
这道题运用了一个套路，当涉及所有人的等待时间之和时，可以考虑提前计算

染色法

一个网格图染色之后是一个二分图是 well-konwn 的

所谓染色，就是把网格图染成国际象棋的棋盘，长这样

黑点和白点组成二分图

具体的染色就是如果\((i+j)\)\(\%\)\(2==10\)，就染成黑色，反之则白

据说还有其他的染色方法，但蒟蒻还没见过

P2774 方格取数问题

正着不好算，就反着来

我们算出最小的不取的方格的和，用总点数减去就可以了

怎么算呢，我们发现，剩下的这些点，一定是与被选的点相邻的

那就好办了，我们将网格染色，黑点放左边，白点放右边，每个黑点向四周的点连一条 inf 边，跑一遍最小割，即为答案

为什么呢，我们这里用到了一个技巧，将被割去的点视为不选的点

如果对于黑点 \(u\)，白点 \(v\)，\(s->u\)，\(v->t\)的边没有被割，而且两点之间有边相连，那就显然有增广路了，明显不符合要求

原文中给予了证明，可以说明所有的符合要求的选点方案对应图上的一个割，所以答案就是总点数减去最小割

其实也很好想

代码

划分问题

强烈推荐 Pecco 的讲解，Link

同时图片来自此 Blog ，侵删