luogu省选计划day1
T1
过水已隐藏
T2
整体二分经典题,主席树上二分也可以
在二分时要算一个国家的每一个出现位置,看起来是不行的但是均摊一下没有问题
使用线段树树状数组辅助计算答案
最大的答案会爆long long,开 ull
#include <iostream>
#include <vector>
#define int unsigned long long
//请注意,这道题longlong都撑不住,要ull
using namespace std;
const int maxN=3*1e5+10;
int n,m,k,idx;
int c[maxN],ans[maxN];//区间修改单点求值BIT
struct node {
int na;
int v;
}q[maxN];
int lx[maxN],rx[maxN],vx[maxN],req[maxN];
vector<int> nation[maxN];
inline int lowbit(int x){
return (-x)&x;
}
inline int query(int x){
//cout << 1 << endl;
int ans=0;
while(x)
ans+=c[x],x-=lowbit(x);
return ans;
}
inline void add(int x,int wh){
//cout << 1 << endl;
//cout << wh << endl;
while(wh<=(maxN))
c[wh]+=x,wh+=lowbit(wh);//cout << wh << endl;
}
inline void change(int l,int r,int v){
add(v,l),add(-v,r+1);
}
void bsearch(int l,int r,int ql,int qr){
//cout <<l << " " << r << ' '<< ql <<" "<< qr << endl;
if(ql>qr) return ;
if(l==r){
// cout << ql << " " << qr << endl;
for(int i=ql;i<=qr;++i)
ans[q[i].na]=l;
return ;
}
int mid=(l+r)>>1;
for(int i=l;i<=mid;++i){
if(lx[i]<=rx[i])
change(lx[i],rx[i],vx[i]);
else{
change(lx[i],m,vx[i]);
change(1,rx[i],vx[i]);
}
}
//cout << query(1) << endl;
vector<node> v1,v2;
for(int i=ql;i<=qr;++i){
int p=0;
//cout << q[i].na << endl;
for(int x:nation[q[i].na])
p+=query(x);//cout << x << endl;
if(q[i].v<=p)
v1.push_back(q[i]);
else q[i].v-=p,v2.push_back(q[i]);
// cout << p << endl;
}
for(int i=l;i<=mid;++i)
if(lx[i]<=rx[i])
change(lx[i],rx[i],-vx[i]);
else
change(lx[i],m,-vx[i]),change(1,rx[i],-vx[i]);
for(int i=0;i<v1.size();++i)
q[ql+i]=v1[i];
for(int i=0;i<v2.size();++i)
q[ql+v1.size()+i]=v2[i];
if(v1.size())bsearch(l,mid,ql,ql+v1.size()-1);
if(v2.size())bsearch(mid+1,r,ql+v1.size(),qr);
}
signed main(){
ios::sync_with_stdio(false);//cin加速
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);//再度加速
//不能用printf,scanf
//强制在线时请勿与'\n'连用
cin >>n >>m;
for(int i=1;i<=m;++i){
int x;
cin >> x;
nation[x].push_back(i);
}
for(int i=1;i<=n;++i){
cin >>q[i].v;
req[i]=q[i].v;
q[i].na=i;
}
cin >>k;
for(int i=1;i<=k;++i)
cin >>lx[i] >> rx[i] >>vx[i];
//cout << 1 << endl;
bsearch(1,k,1,n);
for(int i=1;i<=k;++i){
if(lx[i]<=rx[i])
change(lx[i],rx[i],vx[i]);
else{
change(lx[i],m,vx[i]);
change(1,rx[i],vx[i]);
}
}
for(int i=1;i<=n;++i){
int p=0;
//cout << q[i].na << endl;
for(int x:nation[i])
p+=query(x);
if(p<req[i]) cout << "NIE" << endl;
else cout << ans[i] << endl;
}
return 114514-114514;
}
/*
hello sir ,
make sure that you aren't writing in 空格式。
*/
T3
过水已隐藏
T4
裸的cdq分治三维偏序,但我现在还不会怎么cdq套cdq……
再高维的话就是二维数点的BIT了
可以用bitset并起来乱搞,复杂度\(O(\frac{n^2}{w})\)
但不能直接开 \(n^2\) 的bitset,这样会炸掉
我们可以只开一点点,比如每次开 \(\frac{n}{3}\) 个,清空再算
xpp:四维往上就跑不过暴力了
T5
神奇妙妙题
我们用ST表先预处理一下区间流量最大的东西向道路和南北向道路
在分治之前,先处理出边界的最长距离为0,分治一开始的区间是整个矩阵
我们每一次先选出区间内流量最大的东西向或南北向道路,这代表如果其走入了这条路,不会拐弯,则这条路上的点的最大值就是其到边界两条路中大的那一条,边界的值都已经算出
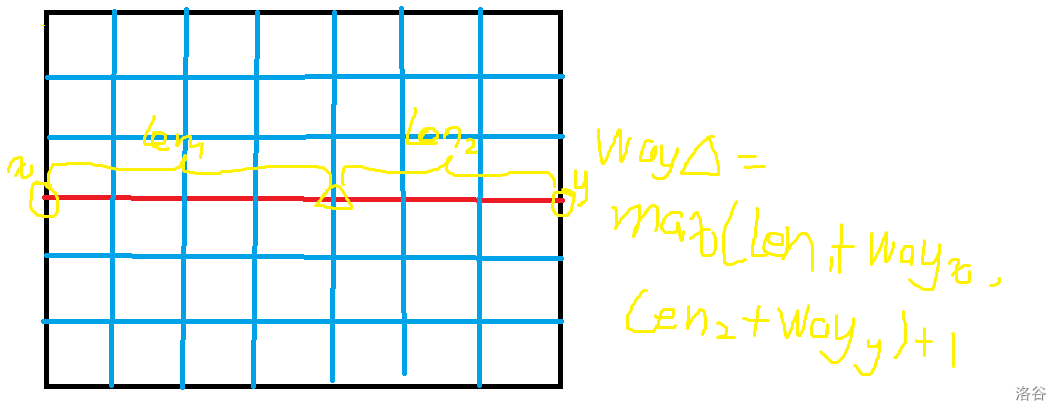
然后这条线会把当前的区间分为两份,继续递归
主定理可得分治的复杂度为\(O(H+W)\)
总复杂度为\(O((H+W)Q)\)
代码细节较多
T6
直接二进制拆分,用ST表预处理
T7
这里我们可以暴力枚举子串的起点
利用字符串匹配的性质,其肯定有单调性,我们进行二分,不断的枚举下一个不同的位置
具体的实现等在研究研究再补
T8
水省
T9
我们可以建一颗后缀树和前缀树,分别跑匹配的前后缀
然后可以利用dfn序的性质,将一个点在前缀树上的dfn序作为横坐标,后缀树为纵坐标
则此题转化为了一个二维数点的问题,将两个子树dfn序的范围取个交,这点分类讨论就可以
然后再将询问离线下来,做扫描线即可
复杂度单log
T10
异或有自反性,这里可以维护一个节点到根的异或和f[i]
则节点 i 到 j 的异或路径和为f[i]^f[j]
将所有的f[i]一起建一颗 01trie,对于每个值贪心选取就行
复杂度线性带 30 的常数
#pragma GCC optimize(2)
#include <iostream>
#include <vector>
#define pii pair<int,int>
#include <bitset>
using namespace std;
const int maxN=1e5+100;
struct node {
int son[2];
}tree[maxN*30];
vector<pii> g[maxN];
int n,f[maxN],idx=1;
bitset<maxN> vis;
void dfs(int now ){
for(pii x:g[now]){
if(vis[x.first]) continue ;
vis[x.first] =1;
f[x.first]=f[now]^x.second;
dfs(x.first);
}
}
void insert(int x){
vector<int> v;
for(int i=1;i<=32;++i){
v.push_back((x&1));
x>>=1;
}
int now=1;
while(!v.empty()){
int p=v.back();
v.pop_back();
if(!tree[now].son[p])
tree[now].son[p]=++idx;
now=tree[now].son[p];
}
}
int enlarge(int x){
int now=1,ans=0;
vector<int> v;
for(int i=1;i<=32;++i){
v.push_back((x&1));
x>>=1;
}
for(int i=31;i>=0;--i){
if(tree[now].son[!v[i]]){
ans+=(1<<i);
now=tree[now].son[!v[i]];
}
else {
now=tree[now].son[v[i]];
}
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);//cin加速
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);//再度加速
//不能用printf,scanf
//强制在线时请勿与'\n'连用
cin >> n;
for(int i=1;i<n;++i){
int u,v,w;
cin >> u >> v >> w ;
g[u].push_back({v,w});
g[v].push_back({u,w});
}
vis[1]=1;
dfs(1);
for(int i=1;i<=n;++i)
insert(f[i]);
int ans=0;
for(int i=1;i<=n;++i)
ans=max(enlarge(f[i]),ans);
cout << ans << endl;
return 114514-114514;
}
/*
hello sir ,
make sure that you aren't writing in 空格式。
*/
T11
可以将柿子转化为\(\sum_{i=1}^{18} [f(a_{i}\, xor\, a_j)=i]*i\)
进一步可以推出\(\sum_{i=1}^{18} [f(a_{i}\, xor\, a_j)\geq i]\)
这里没乘系数,每一个数值会在小于它时多算,所以没有错
这样就可以在 01trie 上小DP一波了,我们枚举 \(10^i\) ,如果基准数当前位置上是 1 就只能走 1,若是 0 ,就把 1 部分的串个数加上,走 0
T12
kmp配合DP
我们定义f[i][j]为 s 走到了 i, t 走到了 j 的次数
如果 \(s_i=t_i\) 则直接转移,如果到了末尾,就答案加一
如果没有匹配,则我们与处理出来一个类似 fail 压缩的写法,找到当前 t 最长的有匹配的 border 进行处理
如果是问号,就枚举起边成哪个字符,用上方方法进行转移

 浙公网安备 33010602011771号
浙公网安备 33010602011771号