小明能把自己拉起来吗？——动滑轮自举问题完整解析

问题描述

小明站在一个立方体上，整个滑轮装置连接在立方体上方，绳子穿过滑轮，滑轮左侧绳子固定在天花板，右侧绳子由小明手持。

核心问题：小明能否通过拉绳子把自己和立方体一起向上提升？

---

0、初步分析

先说结论，只要小明能使出大于【自己+立方体】重量的力，小明就可以把自己拉起来！

• 当小明的手完全不发力，地面对立方体的支持力 F 等于小明和立方体的总重力 G （F=G）。此时，滑轮左侧一端的天花板和右侧一端的手都不提供任何拉力
• 当小明开始手握绳子向上拉，天花板一端绳子明显绷紧，此时左侧天花板提供了一点向上的拉力 T，此时 F + T = G。
• 当小明拉力加大，T 逐渐加大，达到 G 时，地面的支持力 F 减小到 0, 此时立方体和地面只是接触，但是以及 “悬浮” 起来了，此时 T=G
• 当向上的拉力继续变大，变成 T > G，那么整体合力向上，于是有了向上移动的加速度，小明也就把自己和立方体一起抬起来了

是不是觉得很有些反直觉？没关系，看完以下的分析，定能让你 “拨云见日，茅塞顿开” ！

一、静态平衡分析

为了更好地分析这个过程，我们先进行一下立方体刚刚 “悬浮” 起来那一刻，系统局部，和 系统整体 的受力分析

符号定义

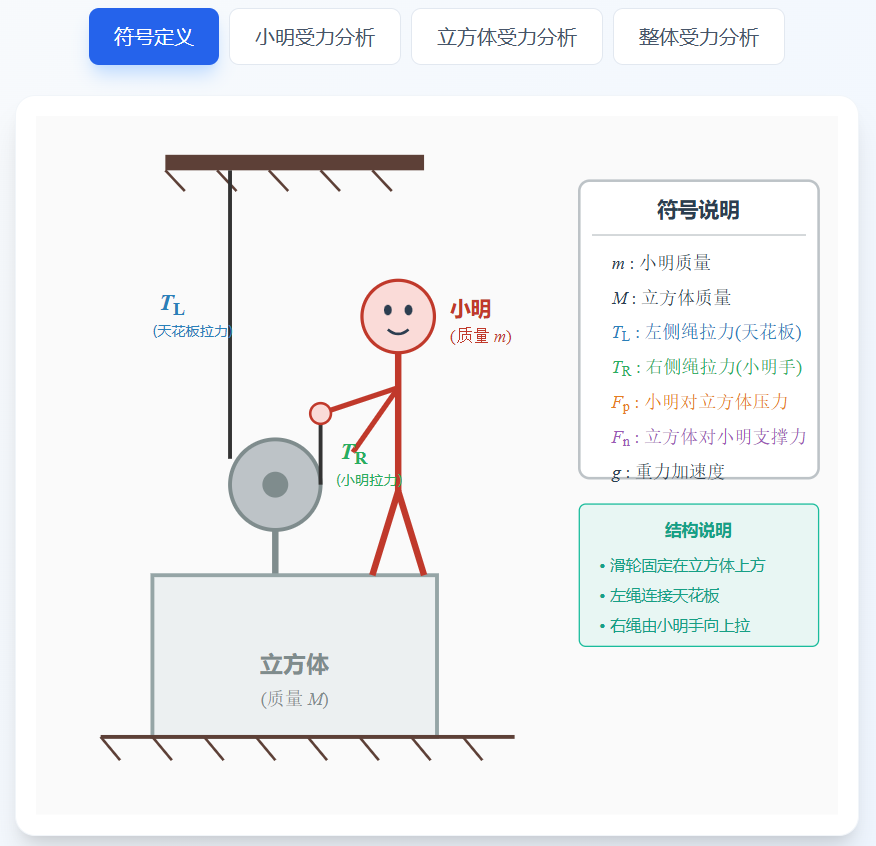
• 小明质量：m
• 立方体质量：M
• 左侧绳子拉力（天花板提供）：TL
• 右侧绳子拉力（小明手拉）：TR
• 小明对立方体的压力：Fp
• 立方体对小明的支撑力：Fn
• 重力加速度：g

1. 对小明的受力分析

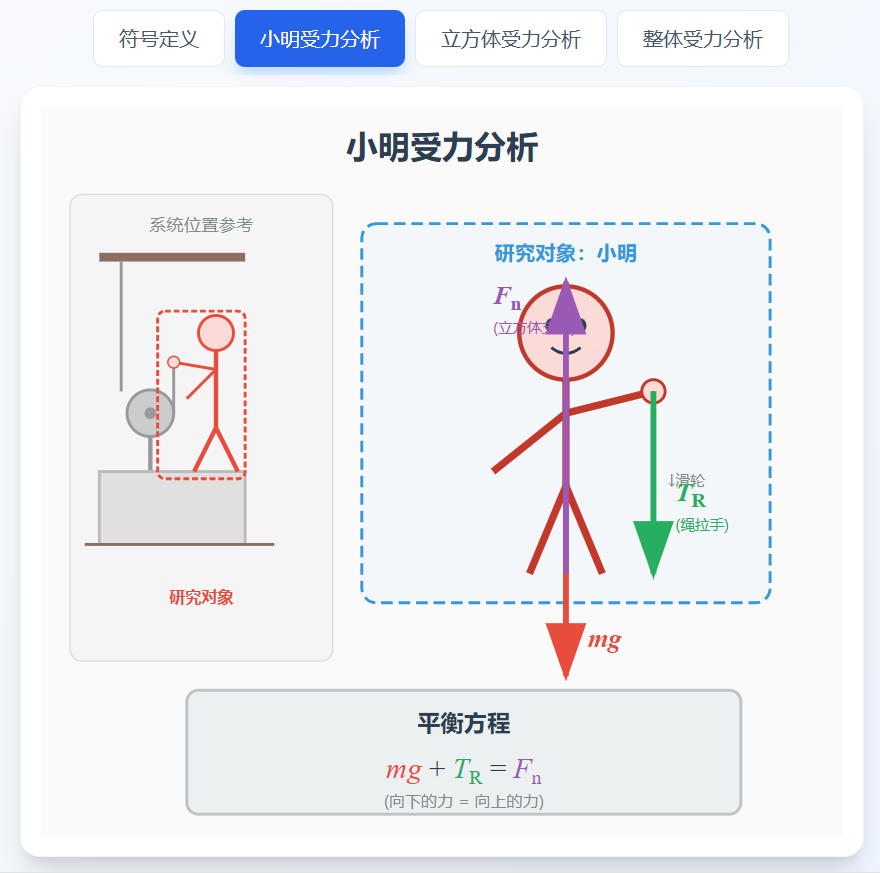
向下的力：

• 重力：mg
• 绳子向下拉力：TR（拉力是相互的）

向上的力：

• 立方体对小明的支撑力：Fn

平衡方程：

[式子1] mg + TR = Fn

2. 对立方体的受力分析

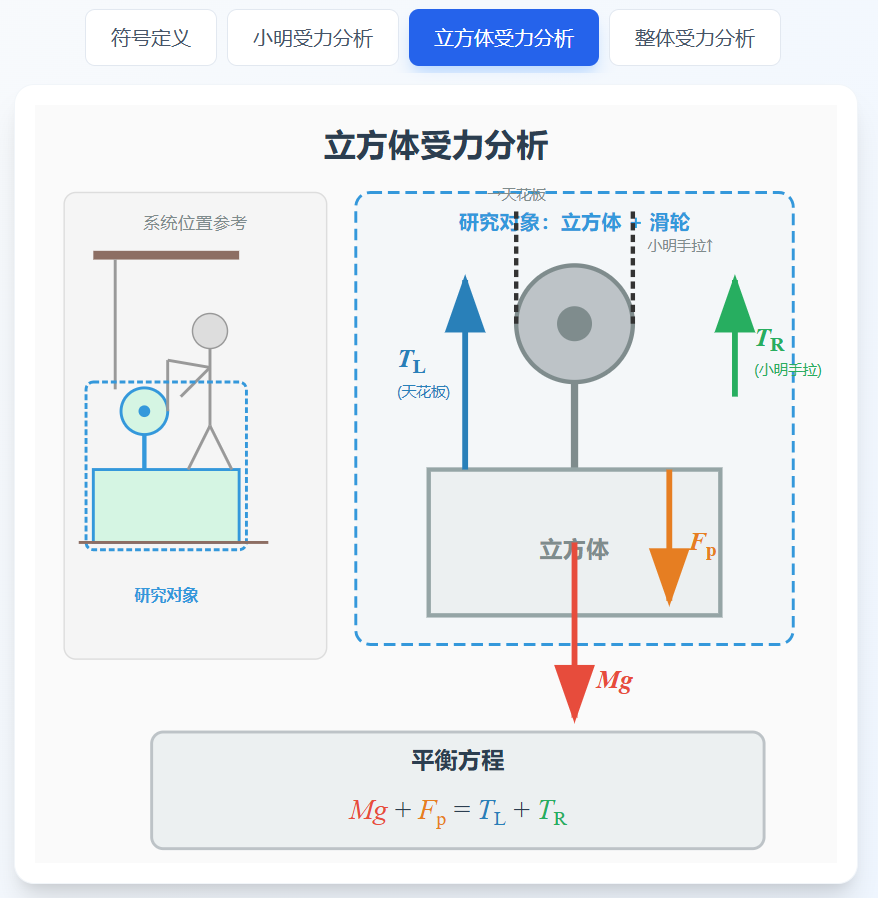
向下的力：

• 立方体重力：Mg
• 小明的压力：Fp（根据牛顿第三定律，Fp = Fn）

向上的力：

• 滑轮两侧绳子的拉力：TL + TR

平衡方程：

[式子2] Mg + Fp = TL + TR

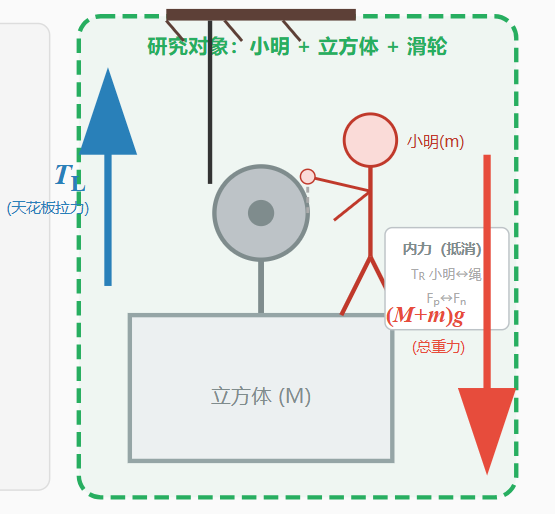
3. 对整体（小明+立方体）的受力分析

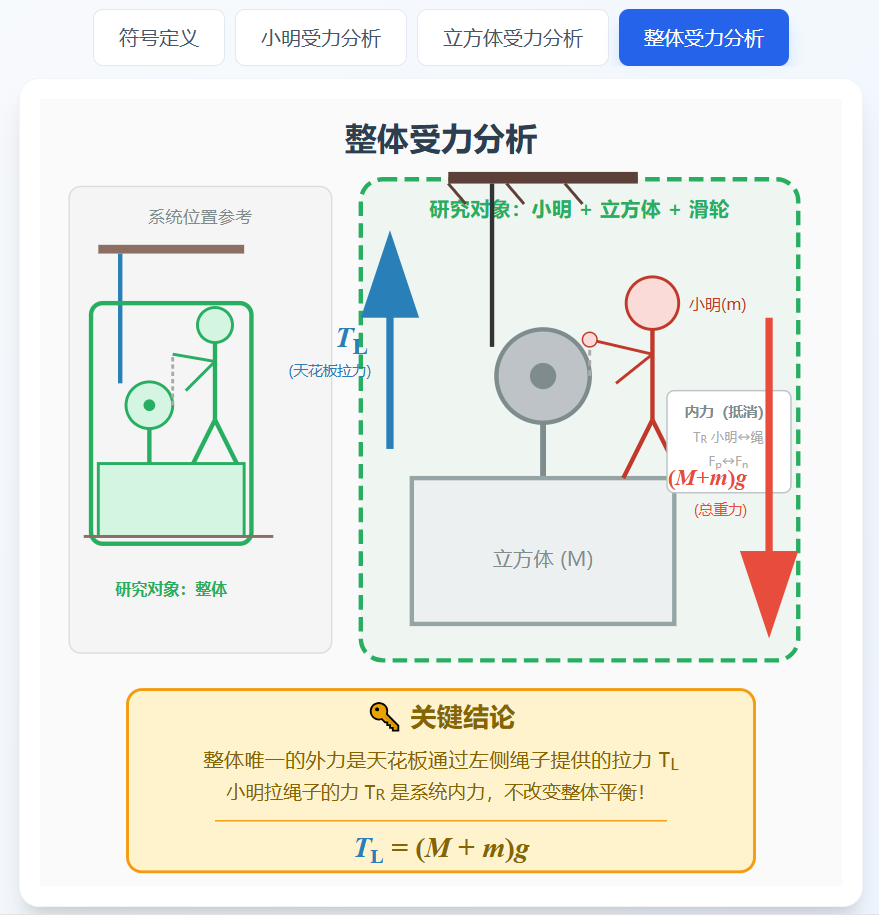
向下的力：

• 总重力：(M + m)g

向上的力：

• 仅有天花板提供的拉力：TL

重点来了：
如果从整体看，唯一的外力是 TL，那么：

[式子3] TL = (M + m)g

这意味着天花板承担全部重量，小明拉绳子只是整个系统的内力，不像我们之前对 常见的动滑轮系统的认识 那样，这里滑轮实际上永远无法分担天花板提升物体的负担。

---

二、动滑轮特点与力平衡分析

理想滑轮的特性

对于理想滑轮（无质量、无摩擦、可自由转动）：

TL = TR

静态平衡时的真实情况

当系统静止时，TL = TR，结合 立方体 受力方程：

[式子2] Mg + Fp = TL + TR

以及 小明 受力方程

[式子1] mg + TR = Fn

并且有，小明对立方体的压力(Fp) = 立方体对小明的支撑力(Fn)

Fp = Fn

可推算如下：

[式子4] Mg + Fp = TL + TR = 2TL

由于 Fp = Fn = mg + TR = mg + TL

将 Fp = mg + TL 代入 [式子4] 得：

Mg + mg + TL = 2TL

移项得：
(M + m)g = 2TL - TL = TL

解得：
TL = (M + m)g

重要结论：天花板承担了全部重量！

这与整体分析的结果一致。

---

三、提升过程的分析

初始状态：立方体刚刚 “悬浮” 起来那一刻

• TL = TR = (M + m)g
• 系统静止平衡，小明提供的拉力 TR，刚刚好等于 [立方体+小明] 的重力

过程：小明加大发力

第1阶段：用力拉绳（TR 增大）

1. 小明肌肉继续加大发力 TR ↑，手臂在右侧向上拉绳子
2. TR 增大↑ > (M + m)g

第2阶段：系统上升

3. 重点来了，此时 左侧连接天花板提供的拉力 TL 由于反作用力，也会跟着加大↑

这就类似与做引体向上时，肌肉收缩 → 拉动骨骼 → 手掌用力抓紧横杆向下拉 → 横杆被动产生向上的反作用力 → 推动身体上升

4. 此时对于 [立方体+小明] 整体： TL > (M + m)g，整个系统获得向上的加速度

5. 滑轮上升，带动立方体和小明一起上升
6. 重力势能增加

第3阶段：重新平衡

7. 小明身体由微微弯腰到挺直后，到达肌肉活动极限
8. TR 逐渐减小，回到 TR = TL = (M + m)g
9. 系统重新静止在更高的位置

能量转换过程

小明肌肉化学能
    ↓
小明对绳子做功
    ↓
系统获得动能（向上运动）
    ↓
系统重力势能增加

关键： 小明通过类似 "挺直腰板" 的动作，肌肉做功转化为系统的重力势能增加（整个过程类似引体向上）。

---

四、为什么能够实现自举？

核心机制

1. 动态过程的力不平衡

   • 滑轮右侧的 TR 加大，带动了左侧 TL 的加大
   • TL > (M + m)g 时，系统向上加速
   • 小明可以通过肌肉做功创造这种不平衡

2. 能量来源

   • 不是"无中生有"
   • 能量来自小明的肌肉（化学能）

五、常见误解澄清

误解1：天花板拉力 = 总重力 / 2

澄清： 如果绳子右侧的绳子也是由 [立方体+小明] 系统之外的力提供，那么，静态平衡时 TL = TR，天花板确实只承担一半重量。但是这里系统整体唯一的向上的力只由天花板提供。

误解2：小明拉绳是内力，无法改变系统运动

澄清： 静态分析是对的，但动态过程中，小明可以通过做功让 TL > (M + m)g，系统获得总体向上的合力。

误解3：这违反了能量守恒

澄清： 完全不违反。能量来自小明的肌肉化学能，转化为重力势能。

---

六、结论

只要小明能使出大于【自己+立方体】重量的力，小明就可以把自己拉起来！

---

本文源地址：https://www.cnblogs.com/BensonLaur/p/19479039