简述-迭代与递归

简述 | 迭代与递归

[!TIP]
在学习几乎所有编程语言的过程中,编写的第一段代码通常是打印"Hello World",这一简单的输出成果，能瞬间为学习者注入信心与动力.
紧随其后的是循环语句和条件语句,它们一起构成了控制程序流程的逻辑核心.它们满足了我们对程序功能的想象:在一定条件下重复处理任务,自动判断并走向不同的执行方向.
很快,递归作为第一个较为复杂的编程概念进入学习者的视野,它以简洁而优雅的方式表达问题的解决思路.

迭代

迭代和循环在本质上是相同的.它们都是通过重复执行某段代码来处理一系列相似的操作.在大多数编程语言中,循环(如 for 循环、while 循环)是实现迭代的语法结构。

for 循环

for i in range(1,10):
    for j in range(1,i+1):
        print(f"{j}X{i}={i*j}", end="\t")
    print()

输出

1X1=1
1X2=2 2X2=4
1X3=3 2X3=6 3X3=9
1X4=4 2X4=8 3X4=12 4X4=16
1X5=5 2X5=10 3X5=15 4X5=20 5X5=25
1X6=6 2X6=12 3X6=18 4X6=24 5X6=30 6X6=36
1X7=7 2X7=14 3X7=21 4X7=28 5X7=35 6X7=42 7X7=49
1X8=8 2X8=16 3X8=24 4X8=32 5X8=40 6X8=48 7X8=56 8X8=64
1X9=9 2X9=18 3X9=27 4X9=36 5X9=45 6X9=54 7X9=63 8X9=72 9X9=81

在这段循环中,我们使用两个 for 循环来打印九九乘法表。外层 for 循环控制行,内层 for 循环控制列。

while 循环

同样的问题,我们还可以使用 while 循环来实现:

i = 1
while i <= 9:
    j = 1
    while j<=i:
        print(f"{j}X{i}={i*j}", end="\t")
        j += 1
    print()
    i += 1

[!NOTE]
while 循环比 for 循环的自由度更高.你不需要事先知道循环的次数,而是根据条件来控制循环的继续或终止.

比如,读取用户输入直到输入特定值：

while True:
    user_input = input("请输入内容|输入'quit'退出: ")
    if user_input == 'quit':
        break
    print(user_input)

递归

递归（recursion）是一种算法策略，通过函数调用自身来解决问题。它主要包含两个阶段。

[!NOTE]

递：程序不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。

归：触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。

下面以一个简单的“斐波那契数列”为例,来看看递归的实现:

[!CAUTION]
给定一个斐波那契数列 \(0,1,1,2,3,5,8,13,\cdots\) ,求该数列的第 \(n\) 个数字。

分析

\(F(1)=0,F(2)=1\)
\(F(n)=F(n-1)+F(n-2),n>2\)

为了得到 \(F(n)\) ,将问题如下分解:

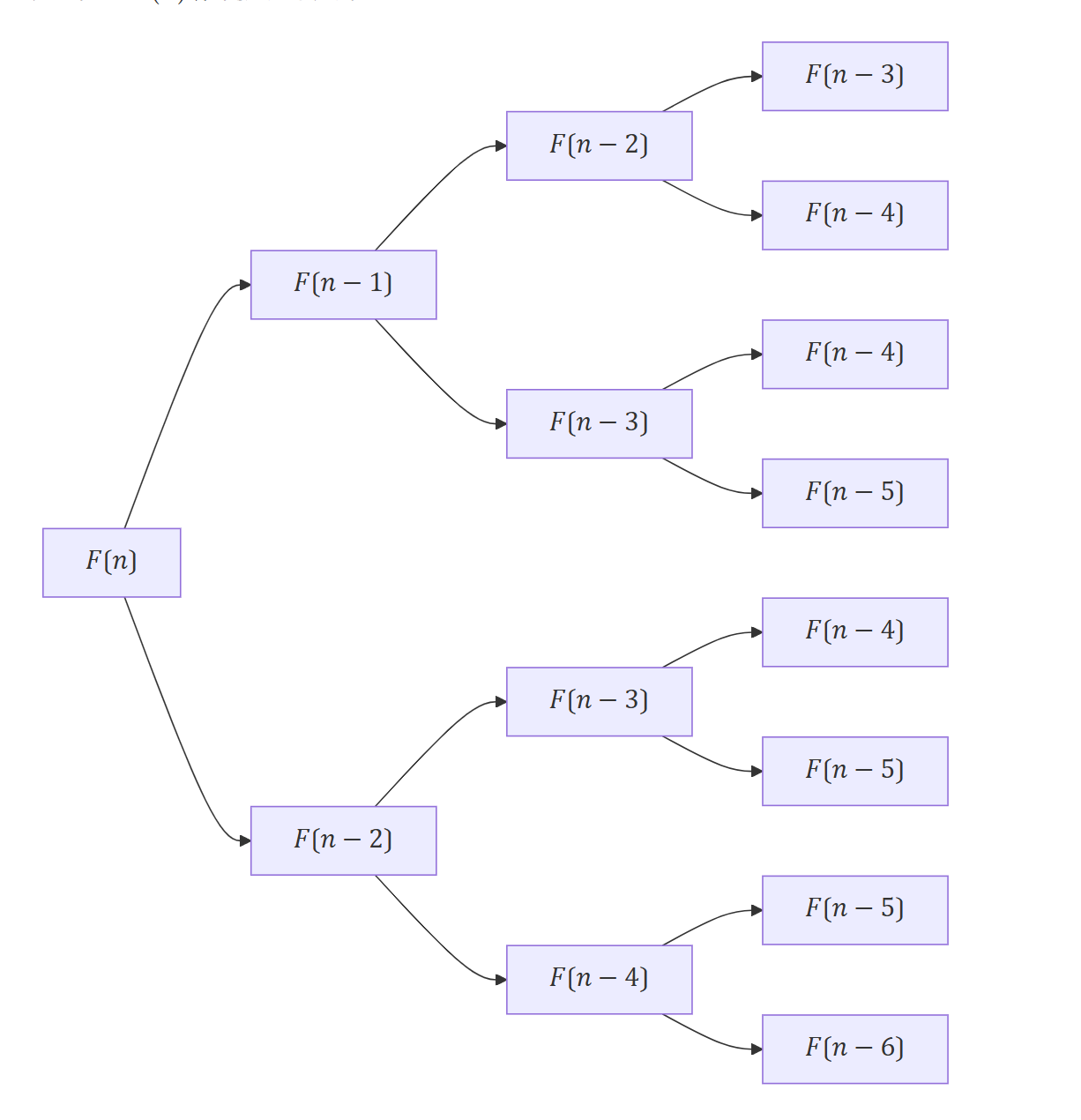
直到 \(F(1)=0,F(2)=1\) ,递结束,然后再一层层往上归(相加),得到 \(F(n)\) 。
代码如下:

def fib(n: int)->int:
    if n == 1 or n == 2:
        return n-1
    return fib(n-1)+fib(n-2)

while True:
    n = int(input("Enter a number: "))
    print(f"The {n}th Fibonacci number is {fib(n)}")

当然也可以用递归来打印九九乘法表:

def Times(n: int = 1, m: int = 1) -> None:
    if n > 9:
        return
    if m <= n:
        print(f"{m}X{n}={m*n}", end="\t")
        Times(n, m + 1)
    else:
        print()
        Times(n + 1,1)

Times()

当然,你没有必要这么折腾自己,适合用循环的地方,还是用循环吧.但如果你想更深入地理解和练习递归,那也可以试试——理论上,迭代和递归都是可以相互转换的.

尾递归

对于普通递归,有以下两点:

每返回到上一级,都会将函数的上下文数据都存储在称为“栈帧空间”的内存区域中,然后继续执行,直至函数返回后才会被释放,这会耗费大量的内存空间。
可能导致大量的重复计算，效率较低。例如，计算 \(fib(5)\) 时，会分别计算 \(fib(4)\)和 \(fib(3)\)，而在计算 \(fib(4)\)时又会计算 \(fib(3)\)和 \(fib(2)\)，这里的 \(fib(3)\)就被重复计算了。

那么,如果函数在返回前的最后一步才进行递归调用,就意味着函数返回到上一层级后,无须继续执行其他操作,因此系统无须保存上一层函数的上下文,从而极大提升了效率。这种情况被称为尾递归（tail recursion）.

那么前面的斐波那契数列的递归函数可以被优化为:

def fib_tail(n: int, a: int = 0, b: int = 1) -> int:
    if n == 1:
        return a
    if n == 2:
        return b
    return fib_tail(n - 1, b, a + b)

while True:
    n = int(input("Enter a number: "))
    print(f"The {n}th Fibonacci number is {fib_tail(n)}")

[!WARNING]
尾递归的优化可以极大地提升效率,但很可惜,Python 解释器本身不支持尾递归优化,从而无法像其他语言那样直接使用尾递归.并且,Python 有一个默认的递归深度限制，通常是 1000。这个限制是为了防止无限递归导致的栈溢出问题。当递归调用的深度超过这个限制时，Python 会抛出 RecursionError 异常。你可以通过 sys.setrecursionlimit 增加递归深度限制，但这样做并不安全。因此,深度较大的递归,还是建议改成使用迭代来实现.

声明

文中 \(pythontutor演示\) 以视频形式呈现,相比 gif,这更容易调整播放进度,如果需要在线演示,请访问https://pythontutor.com/,但网页版的 \(pythontutor\) 访问可能不太稳定.本文中 \(pythontutor\) 代码演示均使用本地版本.
文中代码均在本地 \(python3.8\) 版本上运行.
推荐两个 GitHub 项目:
- hello-algo
- LeetCode-Book
关注公众号 \(BeijiuX\) ,获取更多内容.