少项式 题解

先对题中的限制进行差分将其变成区间限制

对于Subtask1，暴力建出 \(n+k+q+2\) 个点跑最大流。

对于Subtask2，可以发现没有必要建出 \(n\) 个点，直接对 \(q+1\) 个区间建点跑最大流。

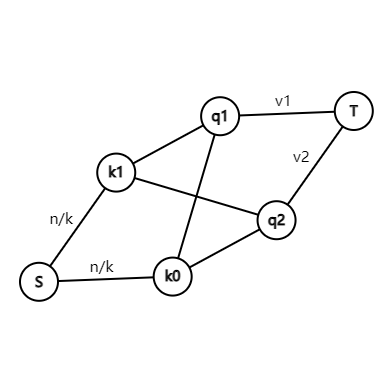
其中 \(v_i\) 表示第 \(i\) 个区间限制的选点数量。

对于Subtask3，考虑最小割。

枚举左边和\(S\)联通的集合\(A\)，那么代价为 \((k-|A|)\cdot\frac{n}{k}+\sum_{j=1}^q\min\{v_j,\sum_{i\in A}w(i,j)\}\)

对上式暴力计算时间复杂度为 \(\mathcal O(2^kq)\)。

对于 Subtask4

记 \(len_j\) 表示第 \(j\) 个区间的长度，那么可以发现 \(w_{i,j}\) 为 \(\left\lfloor\frac{len_j}{k}\right\rfloor\) 或 \(\left\lfloor\frac{len_j}{k}\right\rfloor+1\)。

并且限制为后者的点构成一个区间。

记 \(S_j\) 为第 \(j\) 个区间需要加 \(1\) 的集合，那么上式代价可以改写为，\((k-|A|)\cdot\frac{n}{k}+\sum_{j=1}^q\min\{v_j,|A|\cdot\left\lfloor\frac{len_j}{k}\right\rfloor+|S_j\cap A|\}\)。

可以观察到对于每一个区间 \(\min\) 的取值与 \(A\) 集合中的数具体是什么没有太大关系，重要的是交集大小和 \(|A|\)。

考虑将区间挂在其对应的区间上面。

对应每一个 \(+1\) 区间 \((l,r)\) 预处理当 \(|A|=a\)，交集大小为 \(h\) 时的答案，记为 \(f_{l,r,a,h}\)。

查询的时候枚举集合 \(A\)，对每个 \(+1\) 区间算贡献即可。

因为 \(+1\) 区间最多有 \(O(k^2)\) 种，因此时间复杂度为 \(\mathcal O(qk^2+2^k\cdot k^2)\)。

对于 Subtask5

记 \(w_j=\left\lfloor\frac{len_j}{k}\right\rfloor\)，那么每个原区间的代价为 \(\min\{v_j,aw_j+h\}\)。

考虑每个原区间对其对于的 \(+1\) 区间 \(f_{l,r,a,h}\) 的贡献。

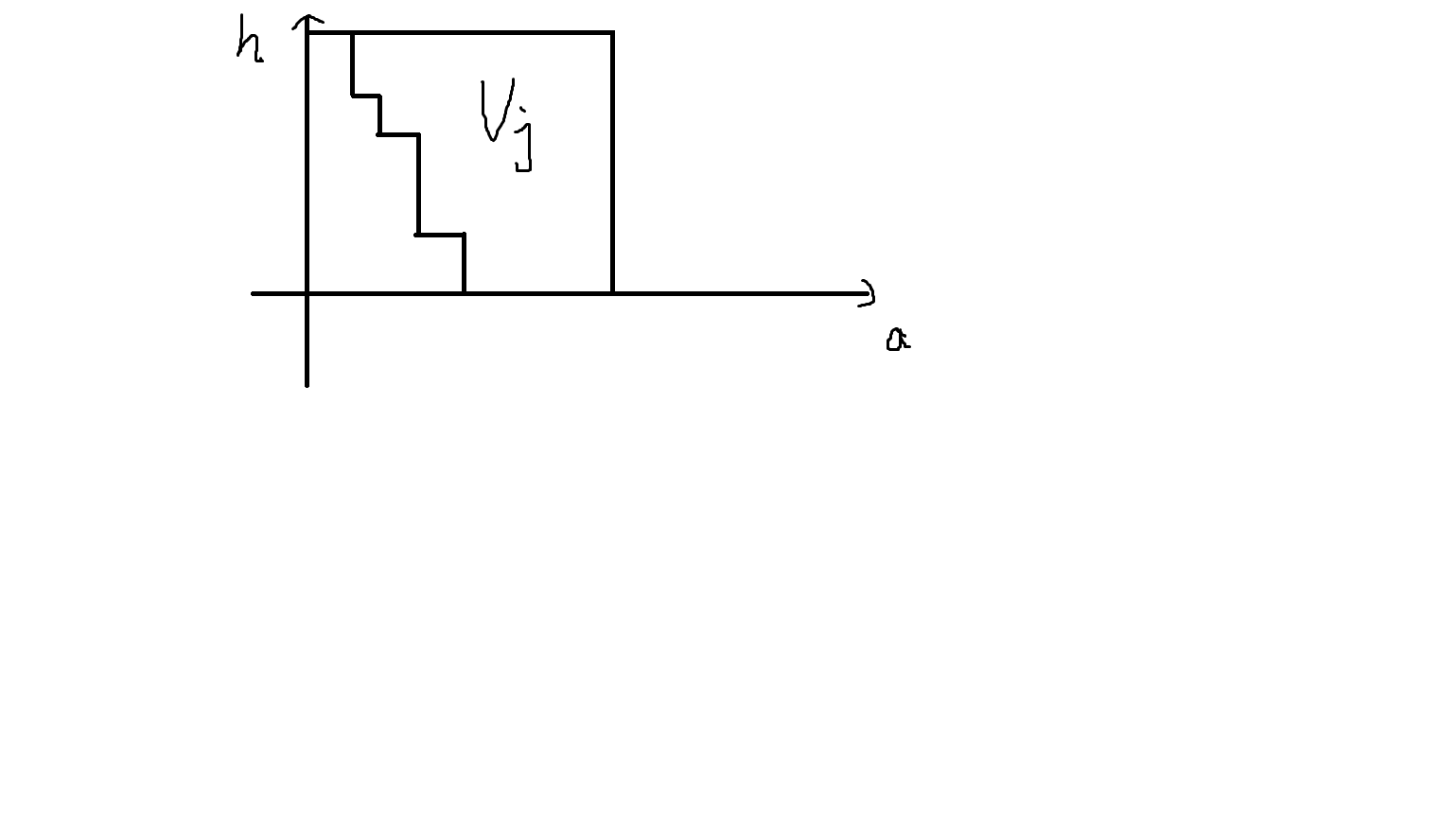
它大致呈一个阶梯状，坐下部分为 \(aw_j+h\)。

那么对于每个 \(a\) 算出分界点进行差分可以做到 \(\mathcal O(qk)\)。

考虑对 \(w_j\) 进行分类，当 \(k\leq w_j\) 时，\(aw_j+h\)的斜率较大，因此贡献图最多出现一个拐点，并且这个拐点可以 \(\mathcal O(1)\) 算出，可以直接差分维护。

当 \(w_j<k\) 时，可以发现 \(v_j\leq len_j\leq k^2\)，也就是这样本质不同的点不超过 \(O(k^5)\) 个，直接计算是矩阵乘法，时间复杂度为 \(\mathcal O(k^7)\)，用前缀和优化可以做到 \(\mathcal O(k^5)\)。

总时间复杂度为 \(\mathcal O(k^5 +q +2^k\cdot k^2)\)。