【Codeforces858F】Wizard's Tour [构造]

Wizard's Tour

Time Limit: 50 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

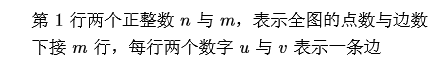
Output

　　

Sample Input

　　4 5
　　1 2
　　3 2
　　2 4
　　3 4
　　4 1

Sample Output

　　2
　　4 1 2
　　4 3 2

HINT

　　

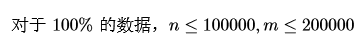
Solution

　　首先，一个连通块的答案可以是floor(m / 2)。考虑如何构造出一种解。

　　首先我们先搞出一个dfs树。

　　那么现在对于一个点，有三种边：1. 非树边；2. 儿子边；3. 父亲边。

　　我们将非树边和儿子边的优先级看做一样的，父亲边优先级最低。

　　考虑将边配给点，即这个点是一种走法中的中点。从叶子节点往上做。两两配对这些边。

　　显然每条边都被尽可能利用了，最后只有与根相连的边可能会有最多一条用不了。

　　这样就是一种解了。

Code

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<vector>
using namespace std;
typedef long long s64;

const int ONE = 400005;
const int MOD = 1e9 + 7;

int get()
{
        int res = 1, Q = 1; char c;
        while( (c = getchar()) < 48 || c > 57)
            if(c == '-') Q = -1;
        if(Q) res = c - 48;
        while( (c = getchar()) >= 48 && c <= 57)
            res = res * 10 + c - 48;
        return res * Q;
}

int ans_len;
struct power
{
        int l, mid, r;
}Ans[ONE * 2];

int n, m;
int x, y;
int next[ONE * 2], first[ONE], go[ONE * 2], tot;
int vis[ONE * 2];

void Add(int u, int v)
{
        next[++tot] = first[u], first[u] = tot, go[tot] = v;
        next[++tot] = first[v], first[v] = tot, go[tot] = u;
}

vector <power> A;
int fat[ONE];

void Dfs(int u)
{
        for(int e = first[u]; e; e = next[e])
        {
            int v = go[e];
            if(fat[v] || vis[e]) continue;
            fat[v] = u, Dfs(v);
        }

        A.clear();
        for(int e = first[u]; e; e = next[e])
            if(!vis[e] && fat[u] != go[e]) A.push_back((power){go[e], 0, e});
        for(int e = first[u]; e; e = next[e])
            if(!vis[e] && fat[u] == go[e]) A.push_back((power){go[e], 0, e});

        int p = 0, len = A.size();
        for(int j = 0; j + 1 < len; j += 2)
        {
            vis[A[j].r] = vis[(A[j].r-1^1)+1] = 1;
            vis[A[j+1].r] = vis[(A[j+1].r-1^1)+1] = 1;
            Ans[++ans_len] = (power){A[j].l, u, A[j + 1].l};
        }
}

int main()
{
        n = get();    m = get();
        for(int i = 1; i <= m; i++)
            x = get(), y = get(), Add(x, y);
        
        for(int i = 1; i <= n; i++)
            if(!fat[i]) Dfs(i);

        printf("%d\n", ans_len);
        for(int i = 1; i <= ans_len; i++)
            printf("%d %d %d\n", Ans[i].l, Ans[i].mid, Ans[i].r);
}