200天1000题 （DAY 3）

200天1000题 （DAY 3）

目前总题数： 12

目前CF分数： 1325

T1.（ABC #072） B.Odd string

/*
	原谅俺，今天课太多了
    开局先水一题
*/
char s[N];
signed main()
{
    cin >> s+1;
    for(int i=1;i<=strlen(s+1);i+=2){
        cout << s[i];
    }
    return 0;
}

T2. (ABC #266) B - Modulo Number

/*
	水题，直接暴力枚举即可
*/
const int N = 1e6 + 10;

const int p = 998244353;

inline void sensei()
{
    int n;
    cin >> n;
    if(n!=0){
        for(int i=0;i<=p;i++){
            if((n-i)%p == 0){
                cout << i << endl;
                return ;
            }
        }
    }
    else{
        cout << "0" << endl;
    }
}

signed main()
{
    sensei();
    return 0;
}

T3. (ABC #266) D. Snuke Panic(1D)

/*
	题目大意：
		一共有5个洞（编号 0 1 2 3 4），高桥的初始位置在0.
		给出N组数，每一组包含三个数据T,X,A
		表示在T时刻编号X的洞会出现一只价值为A的Snuke，如果在那个时刻你在编号X的洞上，那么你就得到了A价值
		每个时刻你只能向左或者向右移动一个单位
		问，你最大能够获得的总价值是多少
*/

/*
	题解：
		有点眼熟的一个DP
		类似kuangbin题单中的"免费馅饼"（ref：https://vjudge.net/contest/68966#problem/G）
		
		做法也是类似的
		定义一个数组f[][]，f[i][j] 表示在i时刻人在j位置能够得到的最大价值
		
		状态转移：
		f[i][j] = max({f[i-1][j-1],f[i-1][j+1],f[i-1][j]}) + g[i][j]
		
		其中特别要注意的是初始条件还有循环时候的边界问题（小心数组越界）
		以及要注意当 j>i时是要 continue掉的
		因为 只用i的时间是到不了一个 编号大于i的点
		
		
		具体见代码
*/

//========================================
const int N = 1e5 + 10;

vector<vector<int>> g(N,vector<int>(6,0));
vector<vector<int>> f(N,vector<int>(6,-inf_ll));

/*
    f[i][j] 表示i时刻在j位置获得的最大值
    
    状态转移：
        f[i][j] = max(f[i-1][j-1] + f[i-1][j+1]) + g[i][j];

    初始化：f[0][1~N] = 0;
*/

inline void sensei()
{
    int n;
    cin >> n;
    
    for(int i=1;i<=n;i++){
        int tt,xx,aa;
        cin >> tt >> xx >> aa;
        g[tt][xx] += aa;
    }
    
    for(int i=0;i<=5;i++) f[0][i] = 0;
    int ans = -inf_ll;
    for(int i=1;i<=100000;i++){
        // 枚举时间t
        for(int j=0;j<=4;j++){
            // 枚举位置 x
            
            if(j > i) continue;
            
            if(j == 0){
                f[i][j] = max(f[i-1][j+1],f[i-1][j]) + g[i][j];
            }else if(j == 4){
                f[i][j] = max(f[i-1][j-1],f[i-1][j]) + g[i][j];
            }else{
                f[i][j] = max({f[i-1][j-1],f[i-1][j+1],f[i-1][j]})+g[i][j];
            }
            ans = max(f[i][j],ans);
        }
    }
    cout << ans << endl;
}

signed main()
{
    sensei();
    return 0;
}

T4. （ABC #266） E. Throwing the Die

/*
	题目大意：
		 输入一个数字N
		 表示最多有N轮
		 你手上有一个骰子，每一轮可以选择投或者不投，如果你选择了不投，那么游戏直接结束，最后投到的数字x（1~6）就是你的最终得分。如果你一直投，那么你最多投N轮，第N轮得到的数字x（1~6）就是最终的得分
		 假设骰子得出每一个数字x（1~6）的概率相同。那么最优情况下的得分的 期望 是多少
*/


/*
	题解，首先考虑贪心
	假设当前的期望是4
	那么对于 投出来是 1 2 3 这样的数字肯定是不如不投（因为会拉低期望，而我们要的是尽量高的分数）
	那么如果是 大于期望的一个数字 例如 5 6 那么我们就投（可以拉高期望）
	
	设f[i]为投到第i轮的期望
	枚举可能投出来的数字 j （1~6）
	按照刚才的策略 加入 j>f[i-1] 那就投 否则就不投
	
	初始状态（也就是只投出一次的期望）        f[1] = (1.0 + 2.0 + 3.0 +4.0 +5.0 +6.0) / 6.0; 
	
	思路如上，详细见代码
*/


const int N = 100 + 10;

vector<double> f(N);

inline void sensei()
{
    int n;
    scanf("%lld",&n);
    f[1] = (1.0+2.0+3.0+4.0+5.0+6.0)/6.0;
    
    for(int i=2;i<=n;i++){
        for(int j=1;j<=6;j++){
            // 枚举可能投出的数字 j
            
            if((double)j >= f[i-1]){
                // 如果j比上一轮期望高，那么就投
                f[i] += ((double)j);
            }else{
                // 否则不如不投
                f[i] += (double)f[i-1];
            }
        }
        // 求本轮期望
        f[i]/=6;
    }
    
    printf("%.10lf\n",f[n]);
}

signed main()
{
    sensei();
    return 0;
}

T5. (ABC #266) C - Convex Quadrilateral

/*
	题意：
		在一个二维平面坐标轴上给出四个点A,B,C,D
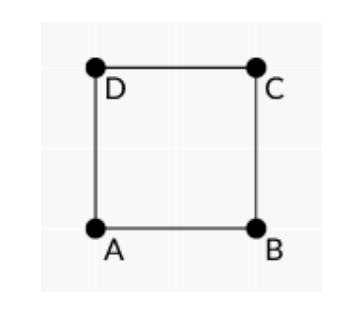
		他们呈逆时针的顺序（见下图）
		
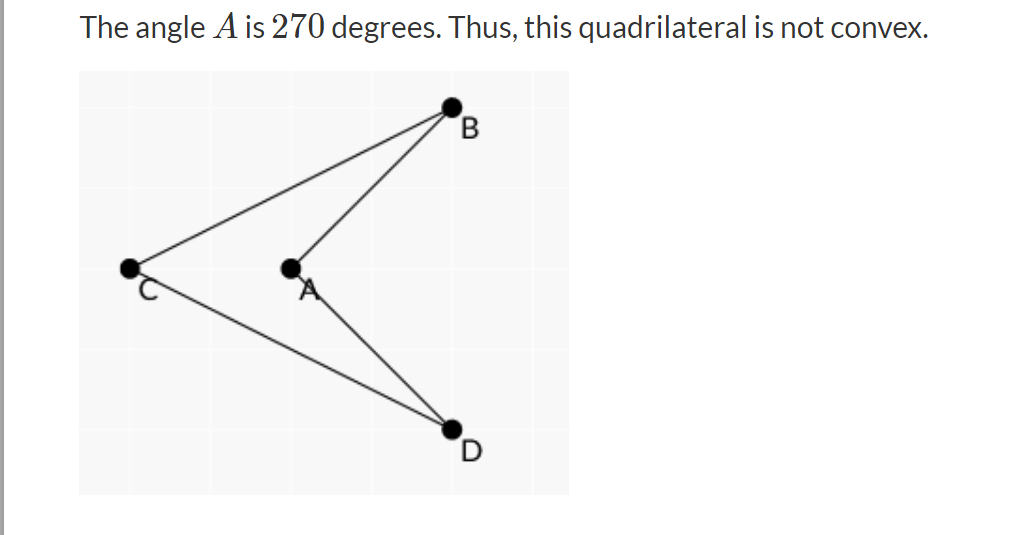
		现在问，在这个A，B，C，D四个点组成的无交叉线的四边形中，有没有一个内角大于180°（见下图）
		有的话输出No 没有的话输出Yes
*/

/*
	题解：
		我们可以考虑使用向量的叉乘
		根据右手螺旋定则再结合本题的题意，当两个向量的叉乘为负数的时候，说明这两个向量构成的内角大于180° 叉乘为0即为等于180 叉乘小于0即小于180°
		根据这个规则枚举每个点即可
*/

struct node{
    int x;
    int y;
};

const int N = 1e6 + 10;

node a,b,c,d;

bool check(node aa,node bb,node cc){
    // check函数 传入三个点，其中 bb 是两个向量的共同点
    // 当叉乘大于0返回true 否则返回false
    int alls;
    int ax = aa.x - bb.x;
    int ay = aa.y - bb.y;
    int bx = cc.x - bb.x;
    int by = cc.y - bb.y;
    
    alls = ax*by - bx*ay;
    if(alls >= 0) return true;
    else return false;
}

inline void sensei()
{
    cin >> a.x >> a.y >> b.x >> b.y >> c.x >> c.y >> d.x >> d.y;
    
    // 枚举所有点作为共同点
    if(check(b,a,d) and check(a,d,c) and check(d,c,b) and check(c,b,a)){
        cout << "Yes" << endl;
    }else {
        cout << "No" << endl;
    }
}

signed main()
{
    sensei();
    return 0;
}