Back to Basics: Let Denoising Generative Models Denoise

Back to Basics: Let Denoising Generative Models Denoise

JIT：验证简单的Transformer能否搭建扩散模型
代码仓库

动机

扩散模型的推理过程可以看作是多步的去噪。本文作者认为，对于去噪模型而言，自然图像的分布为一个低维流形，而噪声则是更加均匀地分布在高维空间。因此，去噪模型的输出设置为自然图像可能更容易训练。本文便是在验证这一猜想。

方法

背景

考虑有数据分布\(x \sim p_{data}(x)\)、噪声\(\epsilon \sim p_{noise}(\epsilon)\)，t时刻的带噪样本\(z_t\)定义为\(z_t = tx + (1-t)\epsilon\)，其中\(log(t) \sim \mathcal{N}(\mu, \sigma)\)。此时，流速定义为\(v=x-\epsilon\)。

现有的方法，按网络输出内容的不同可分为三种：

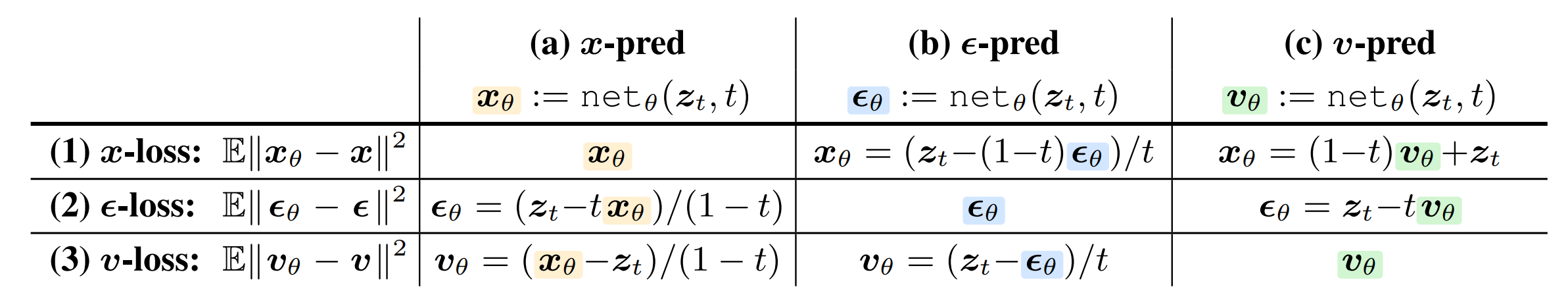
Toy Experiment

作者构建了一个简单的实验验证猜想。首先从二维流形采样数据，再通过固定的随机矩阵投影到\(D\)维，并添加噪声。训练生成模型去噪。

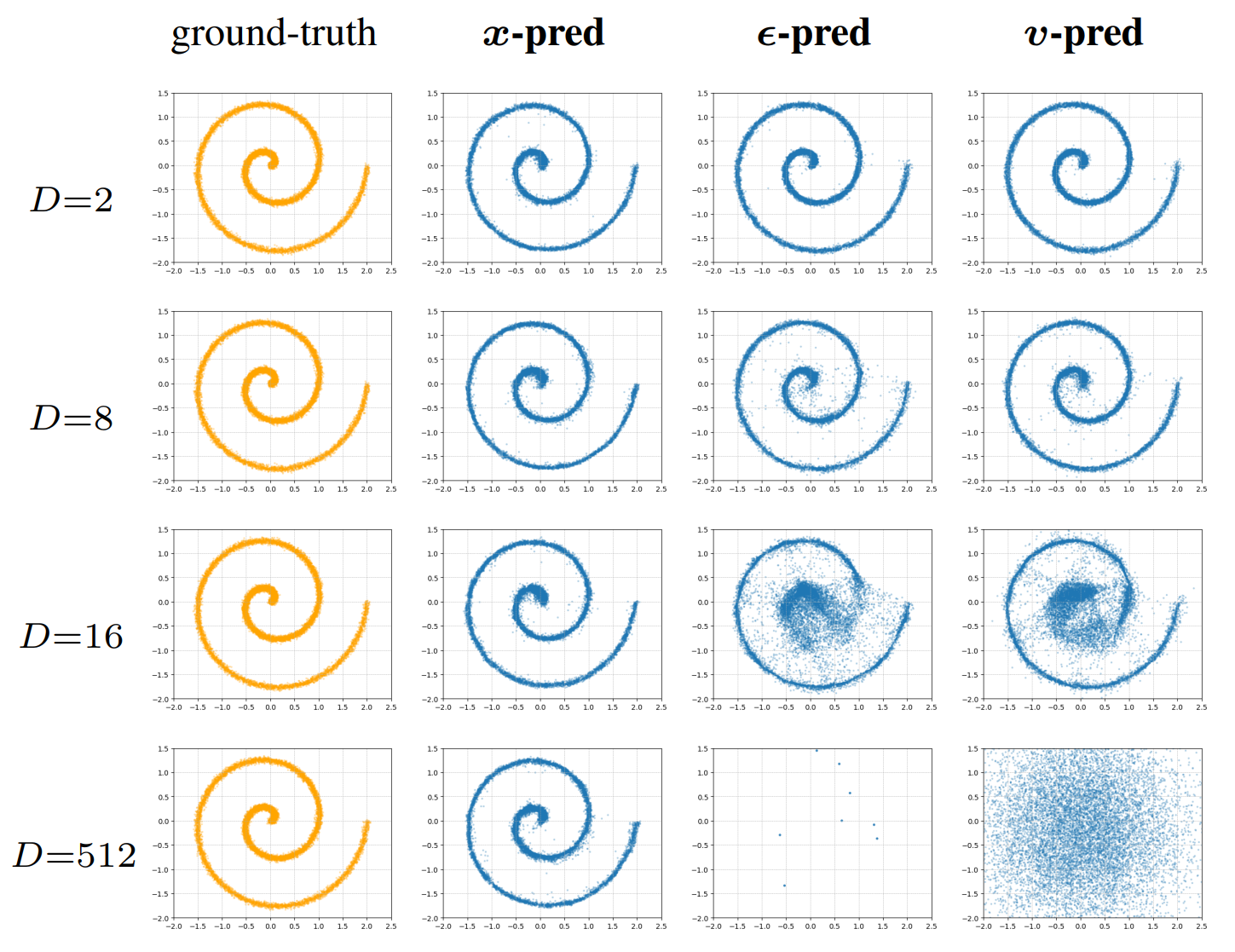
结果展示，当\(D\)增大时，只有x-prediction模型能产生合理的结果。

模型

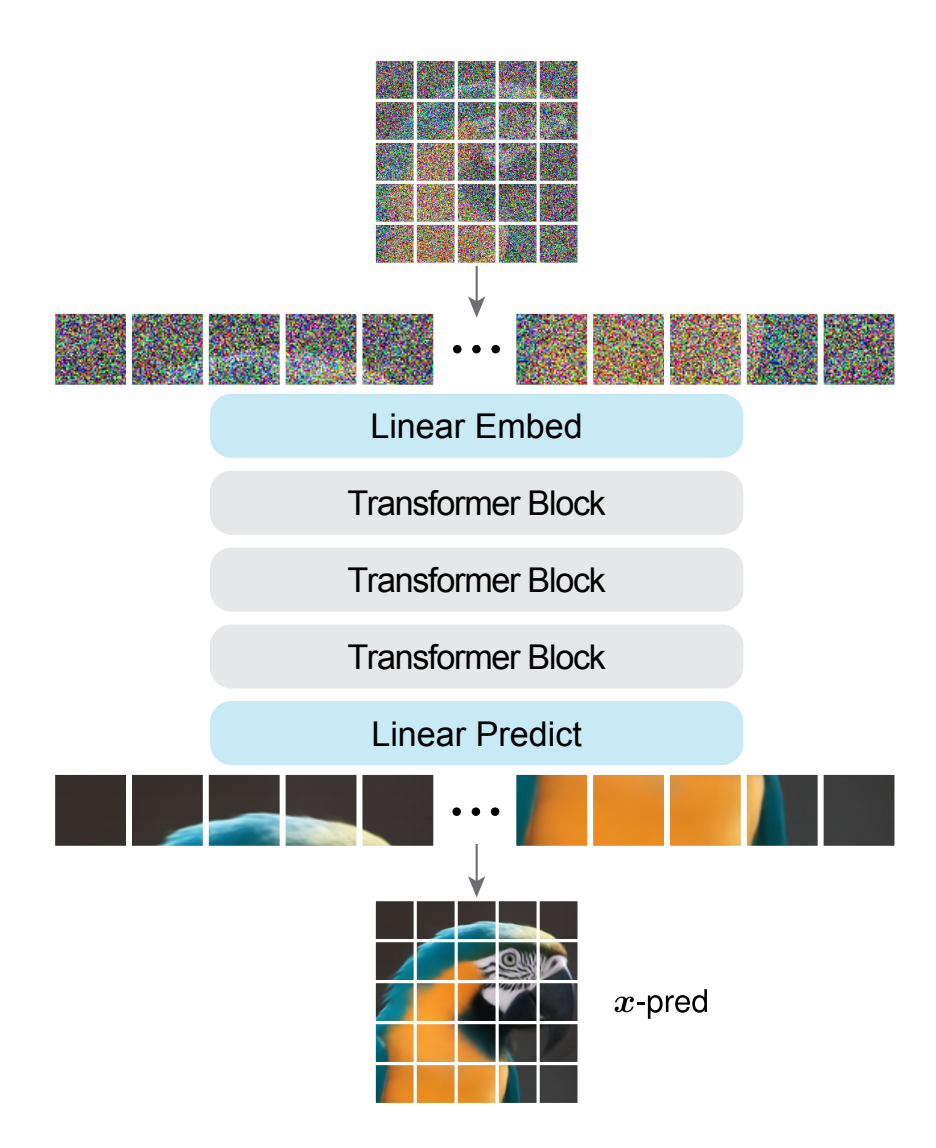
基本类似ViT的结构。输入图像被划分为若干不重叠的Patch，通过线性嵌入映射、位置编码、Transformer block堆叠、线性预测一系列结构直接输出去噪后的图像。

影响因素分析

文中对多种可能影响模型性能的因素进行了分析，首先通过实验证明在ImageNet上，\(256 \times 256\)尺寸下确实只有x-prediction方案有效。而\(64 \times 64\)下则差异不大。作者认为这是因为在低维度下，噪声分布的问题没有严重到影响模型性能。这也解释了为什么现有的一些模型没有观测到预测噪声带来的问题———许多latent扩散模型是在低维度下进行的。

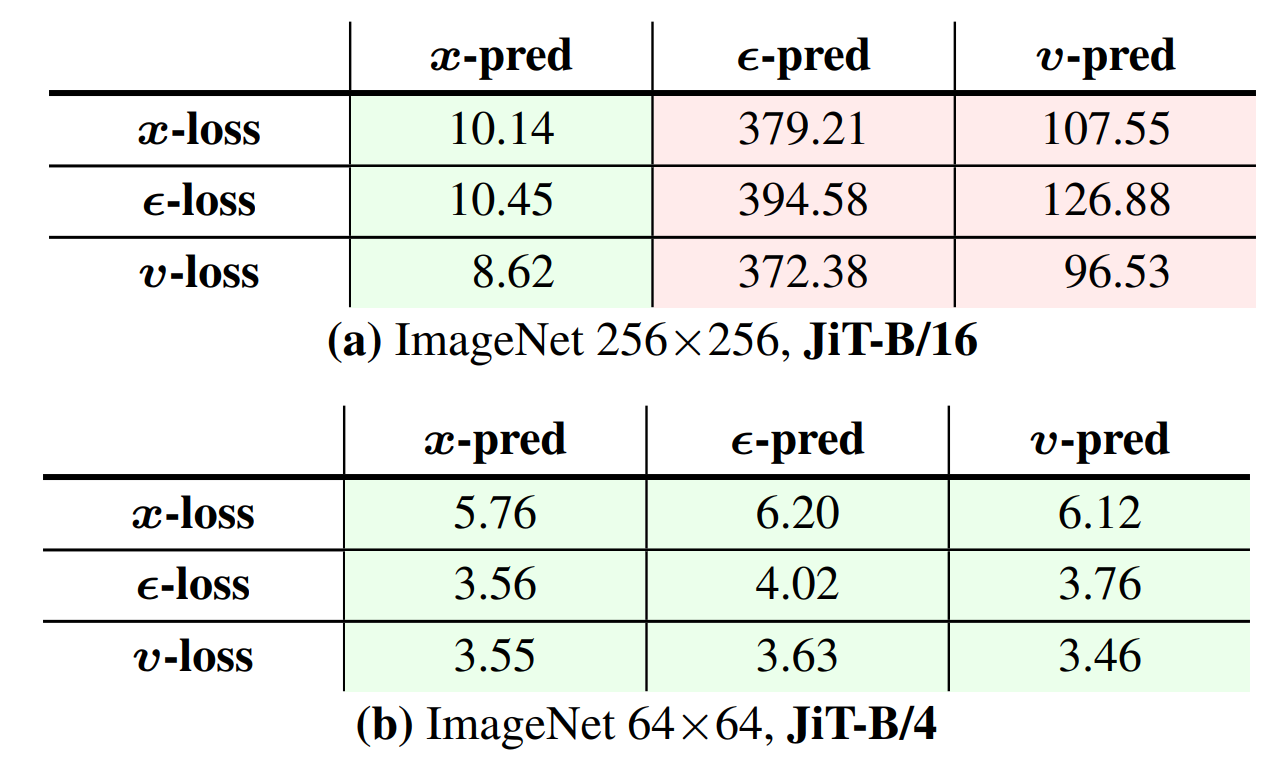
文中还验证了其它诸多因素，这里不一一详述，简单总结就是：

• 损失权重、噪声等级偏移、隐藏神经元个数不充分
• Bottleneck结构有效，因为其能学习到低维表征

实验

作者测试了ImageNet中不同尺寸下的生成结果，发现本文方法JiT在没有使用预训练的前提下，性能指标和计算量都没有大幅变化。

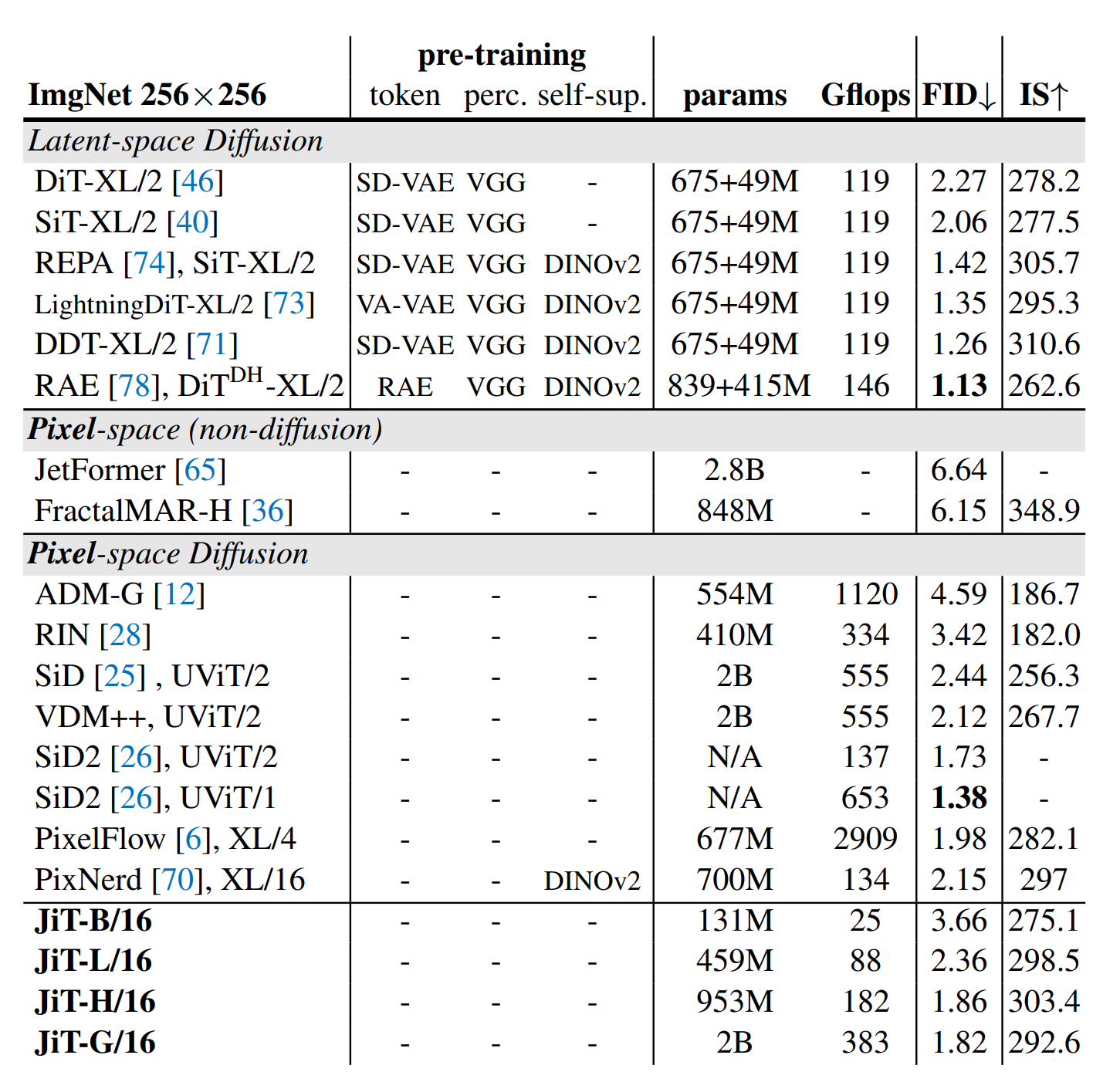
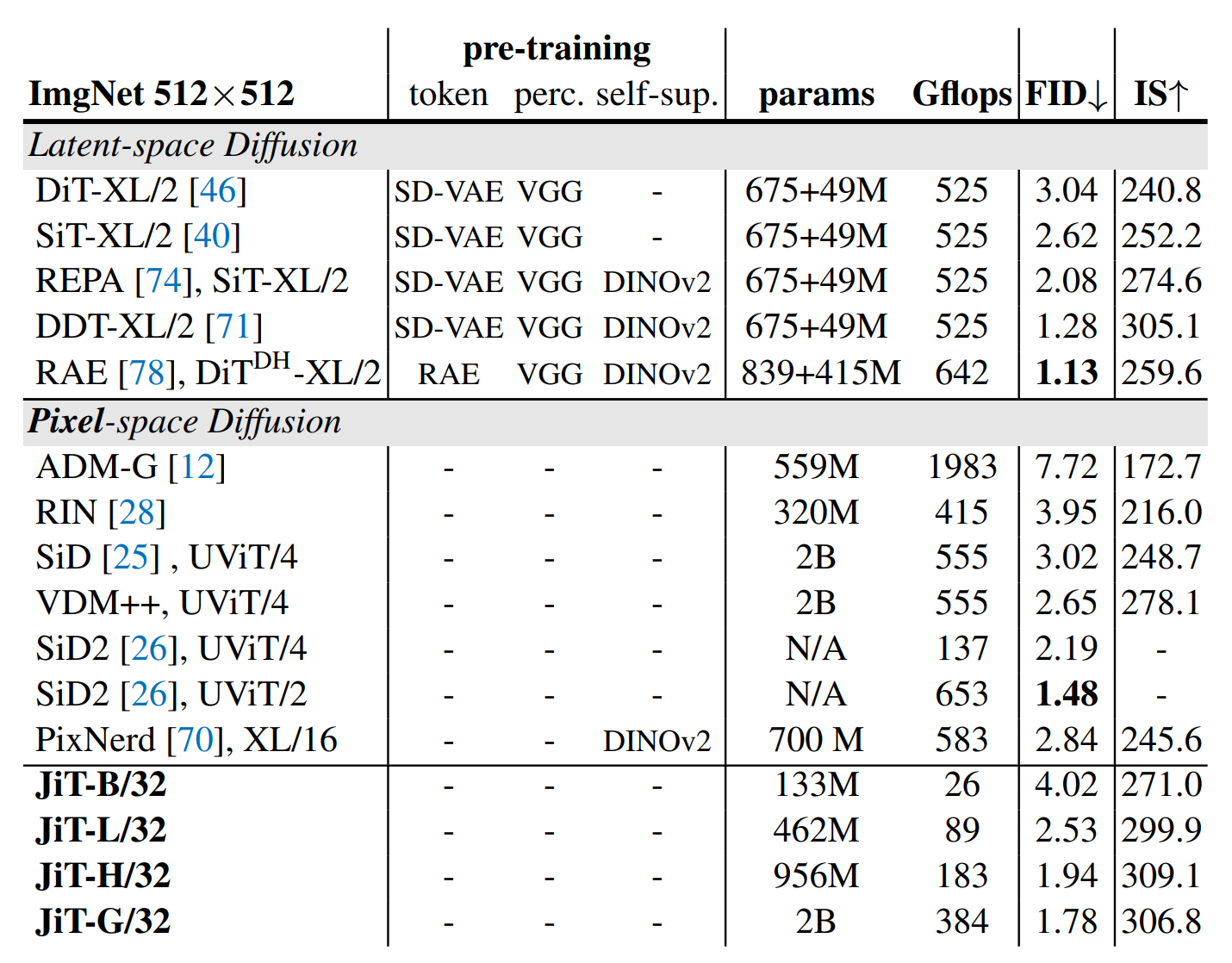
总结

作者认为，过去扩散模型的发展主要聚焦于概率公式（probabilistic formulation）上，而对网络结构的能力或者局限关注较少。而本文则是立足于网络预测目标，简单调整了网络结构，并在此基础上验证了多种因素，最终得出了一个符合逻辑的结论：网络预测噪声分布比预测真实数据分布更难。

笔者对扩散模型以及去噪这一领域的发展并不算非常熟悉。但就模糊的印象中，去噪领域输出真实图像或者输出残差/噪声的做法应该都是存在且常见的。倒是真没想到在扩散模型领域，这一点之前没有深入的实验和研究。

本文的风格和该团队之前的一些文章还是蛮相似的，基本思路是一个符合逻辑的假设辅以大量实验验证以及一些数学证明，最终得到一个优雅又可信的结论。