LongNet: Scaling Transformers to 1,000,000,000 Tokens

LongNet: Scaling Transformers to 1,000,000,000 Tokens

LongNet：通过类似线段树的形式构建自注意力的稀疏掩码，从而降低长序列下的计算复杂度

动机

本文旨在降低注意力的计算复杂度，从而实现对长序列处理的支持。本文方法成功将可处理的序列长度拓展到了十亿（1 billion）。

方法

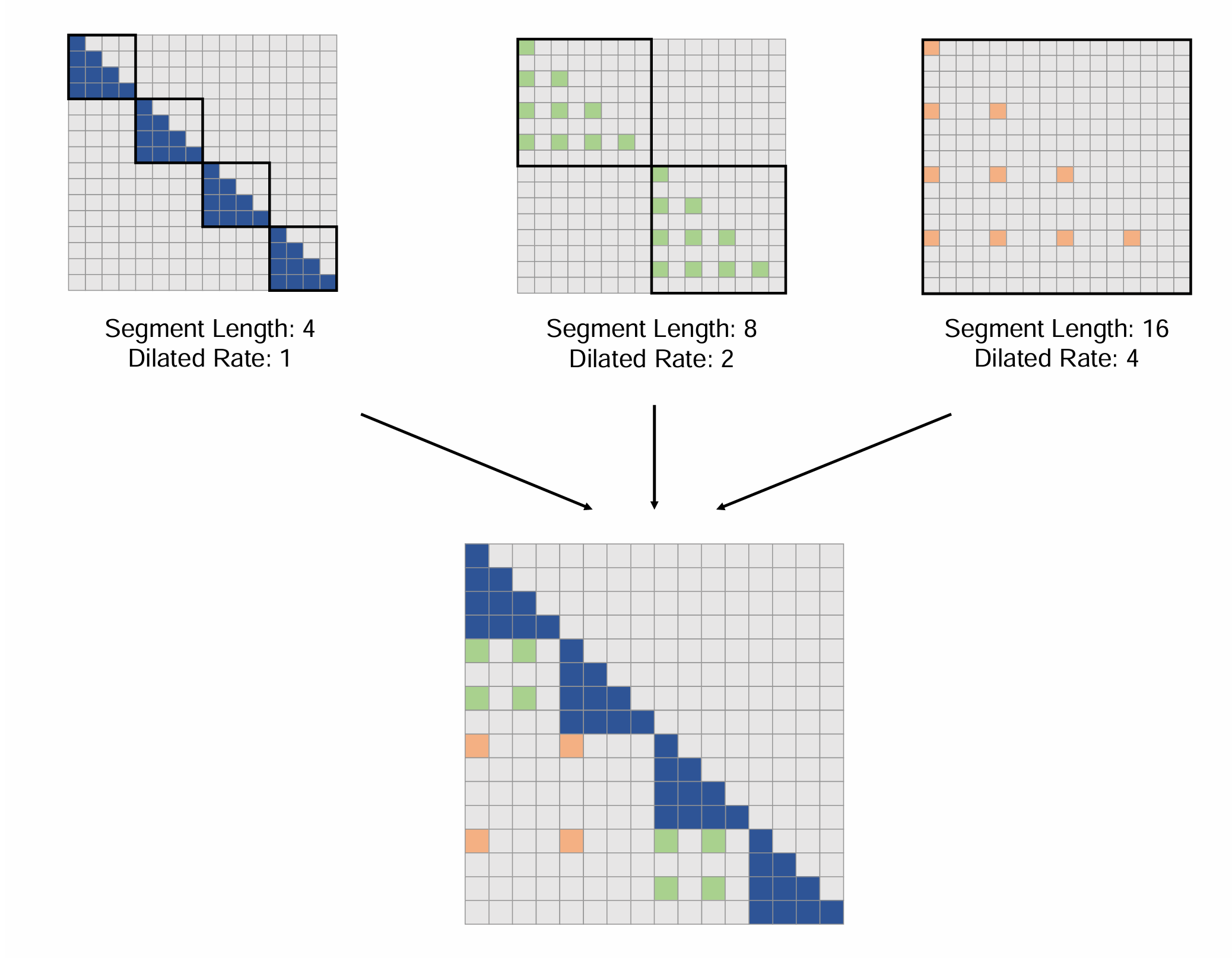
本文的核心思路是参考线段树的构造方式，将指数级变化的稀疏掩码组合在一起。

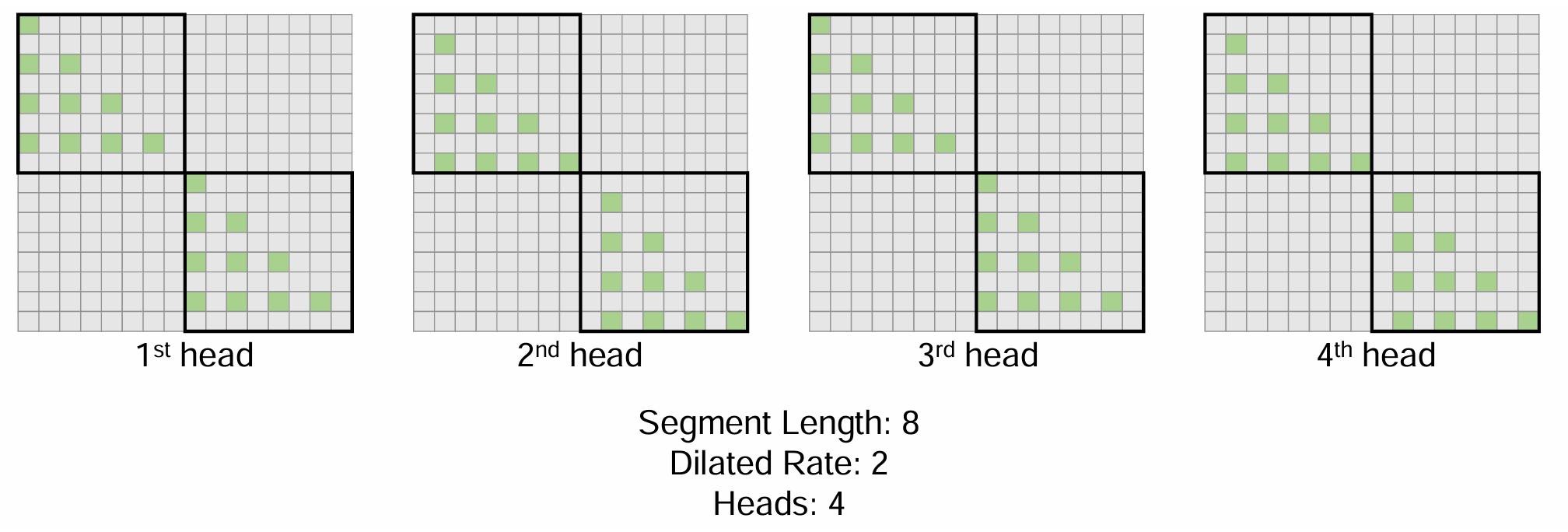
多头的情况下会进行一些移位。

假设序列长度为\(N\)，特征维度为\(d\)，分段尺寸（segment size）为\(r\)，空洞率（dilated rate）为\(w\)，则计算复杂度为：

\[FLOPs=\frac{2N}{w}(\frac{w}{r})^2d=\frac{2Nwd}{r^2} \]

如果采用多种\((r,w)\)的设置：

\[FLOPs=2Nd\sum^k_{i=1}{\frac{w_i}{r_i^2}} \]

令\((r,w)\)增长的倍率为\(\alpha>1\)：

\[FLOPs=2w_0Nd\sum^{k-1}_{i=0}{\frac{1}{\alpha^i}} \leq \frac{2\alpha}{\alpha-1}w_0Nd \]

从计算复杂度估计的角度来看，\(\alpha\)和\(w_0\)的取值通常都比较小且远小于\(N\)和\(d\)，可视为常数。所以最终的计算复杂度估计可近似为\(\mathcal{O}(Nd)\)

实验

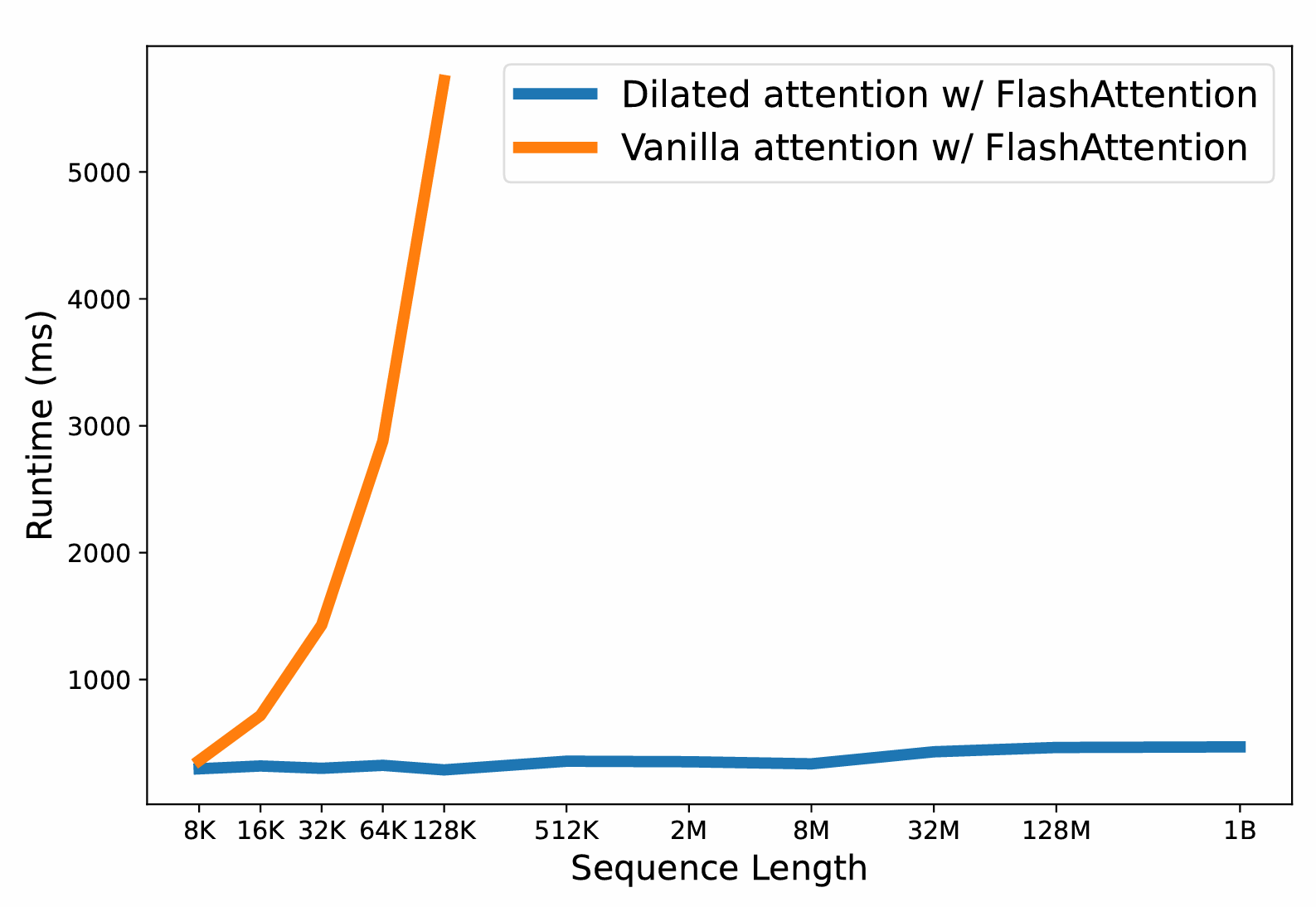
有明显的计算效率改善。

应用

Prov-GigaPath将超高分辨率的病理切片图像切分为若干小块，每块视为一个token，形成一个长序列，由此适配本文方法。

总结

本文的亮点在于对超长序列的支持。这一特点在许多热门领域不算特别有用，毕竟1B长度的token序列还是比较少见，本文似乎也没有在学术刊物上发表。但是其在特定领域还是能够发光发热，最终获得令人瞩目的成果，或许这就是技术积累的意义。