TensoRF: Tensorial Radiance Fields

TensoRF: Tensorial Radiance Fields

TensoRF：利用一维和二维张量的外积表示三维的特征
代码仓库

动机

CP分解：一个三维张量\(\mathcal{T}\in\mathbb{R}^{I\times J \times K}\)可以表示为一维张量外积的和：

\[\mathcal{T}=\sum^R_{r=1}{\mathbf{v}_r^1\circ\mathbf{v}_r^2\circ\mathbf{v}_r^3} \]

其中，三个一维向量\(\mathbf{v}_r^1\in\mathbb{R}^{I}\)、\(\mathbf{v}_r^2\in\mathbb{R}^{J}\)、\(\mathbf{v}_r^3\in\mathbb{R}^{K}\)。

本文则在此基础上提出了通过一维向量和二维矩阵的外积表示三维张量的VM分解（vector-matrix decomposition）：

\[\mathcal{T}=\sum_{r=1}^{R_1}{\mathbf{v}_r^1\circ\mathbf{M}_r^{2,3}} + \sum_{r=1}^{R_2}{\mathbf{v}_r^2\circ\mathbf{M}_r^{1,3}} + \sum_{r=1}^{R_3}{\mathbf{v}_r^3\circ\mathbf{M}_r^{1,2}} \]

其中，\(\mathbf{M}_r^{2,3}\in\mathbb{R}^{J\times K}\)、\(\mathbf{M}_r^{1,3}\in\mathbb{R}^{I\times K}\)、\(\mathbf{M}_r^{1,2}\in\mathbb{R}^{I\times J}\)，三个矩阵的秩不作限定。总体而言，能够使用更少的成分，并且能够通过\((R_1,R_2,R_3)\)分别控制三个维度的复杂度。

假设\(R_1=R_2=R_3=R\)，且令\(\mathcal{A}_r^a=\mathbf{v}_r^a\circ\mathbf{M}_r^{b,c}\)，则可以表示为：

\[\mathcal{T}_{ijk}=\sum_{r=1}^R\sum_m{\mathcal{A}^m_{r,ijk}} \]

方法

模型框架

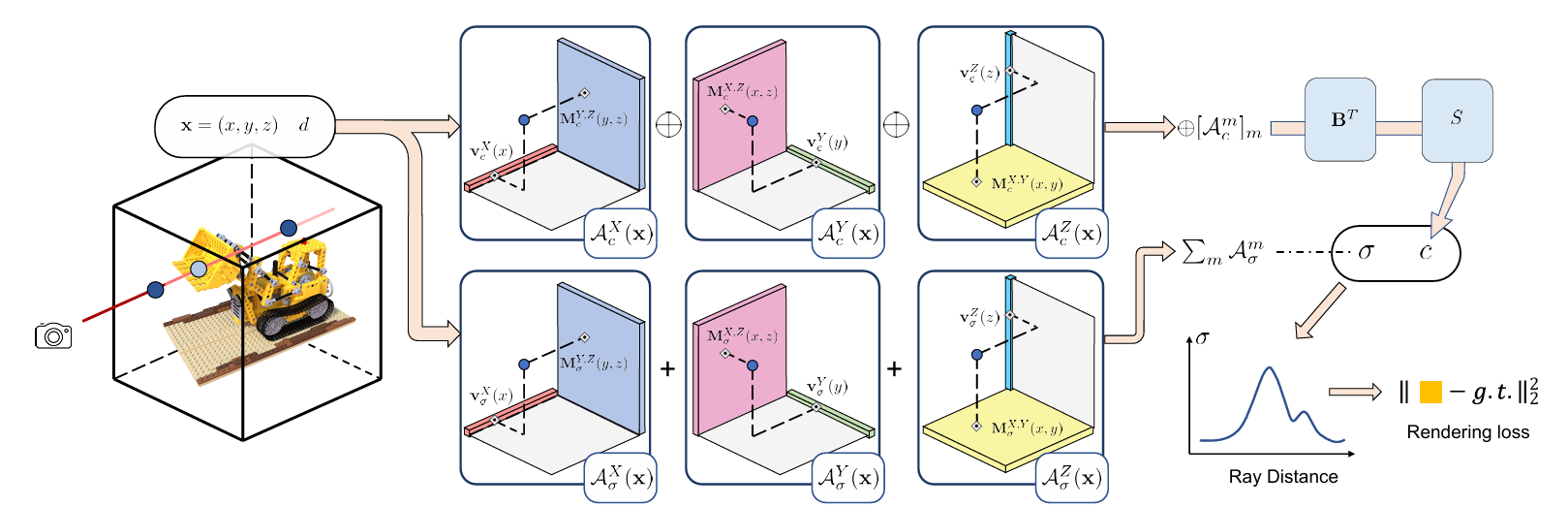
在三维\(XYZ\)场景重建的场景下，假设有坐标点\(\mathbf{x}=(x,y,z)\)，沿方向\(d\)得到视体素密度\(\sigma\)与视角对应的颜色\(c\)。

假设有两个网格\(\mathcal{G}_{\sigma}\)、\(\mathcal{G}_c\)分别对应密度与颜色的特征，则采样过程可以表示为：

\[\sigma, c = \mathcal{G}_{\sigma}(\mathbf{x}),\mathcal{S}(\mathcal{G}_c(\mathbf{x}),d) \]

其中，\(\mathcal{G}_{\sigma}(\mathbf{x})\)和\(\mathcal{G}_c(\mathbf{x})\)表示在两个网格上的\(\mathbf{x}\)位置做三线性插值，\(\mathcal{S}\)可以是一个小的MLP或球谐函数（spherical harmonics functions, SH）。

根据VM分解，\(\mathcal{G}_{\sigma}\)、\(\mathcal{G}_c\)可以表示为若干一维张量\(\mathbf{v}\)和二维张量\(\mathbf{M}\)的外积的和（此处公式略）。

具体实现中，\(\mathcal{G}_{\sigma}\)直接通过VM分解表示：

\[\mathcal{G}_{\sigma,ijk}=\sum_{r=1}^{R_{\sigma}}\sum_{m\in XYZ}{\mathcal{A}^m_{\sigma,r,ijk}} \]

而\(\mathcal{G}_c\)则是通过一个矩阵\(\mathbf{B}\)进行映射：

\[\begin{array}{rl} \mathcal{G}_{c,ijk} = & \mathbf{B}(\oplus[\mathcal{A}^m_{c,ijk}]_{m,r}) \\ = & \sum_{r=1}^{R_c}{\mathcal{A}^X_{c,r,ijk}\mathbf{b}_{3r-2} + \mathcal{A}^Y_{c,r,ijk}\mathbf{b}_{3r-1} + \mathcal{A}^Z_{c,r,ijk}\mathbf{b}_{3r}} \end{array} \]

其中，\(\mathbf{B}\)由所有\(\mathbf{b}_a\)堆叠而成。

插值

在位置\(\mathbf{x}={x,y,z}\)上的采样过程可以表示为：

\[\mathcal{A_r^X}(\mathbf{x})=\mathbf{v}_r^X(x)\circ\mathbf{M}_r^{YZ}(y,z) \]

插值过程在\(\mathbf{v}\)和\(\mathbf{M}\)上进行，以此减少需要的点的数量，进而提高运算效率。

体素渲染

参照NeRF，在射线上采样\(Q\)个点，并计算颜色\(C\)：

\[C=\sum^Q_{q=1}{\tau_q(1-\exp(-\sigma_q\Delta_q))c_q},\tau_q=\exp(-\sum^{q-1}_{p=1}{\sigma_p\Delta_p}) \]

其中，\((\sigma_q,c_q)\)表示采样位置\(\mathbf{x}_q\)上的密度和颜色，\(\Delta_q\)是射线步长，\(\tau_q\)为透过率。

重建

给定一组多视角、已知相机位姿的图像，通过最小化L2损失进行梯度下降，仅监督GT像素颜色。

为了防止过拟合，对向量和矩阵加了L1正则化与TV（total variation）损失。然而，在真实数据集上，TV损失比L1正则化损失更有效。

为了进一步提升性能且避免局部最小，通过插值上采样向量和矩阵，从而实现“corse-to-fine”重建。

实验

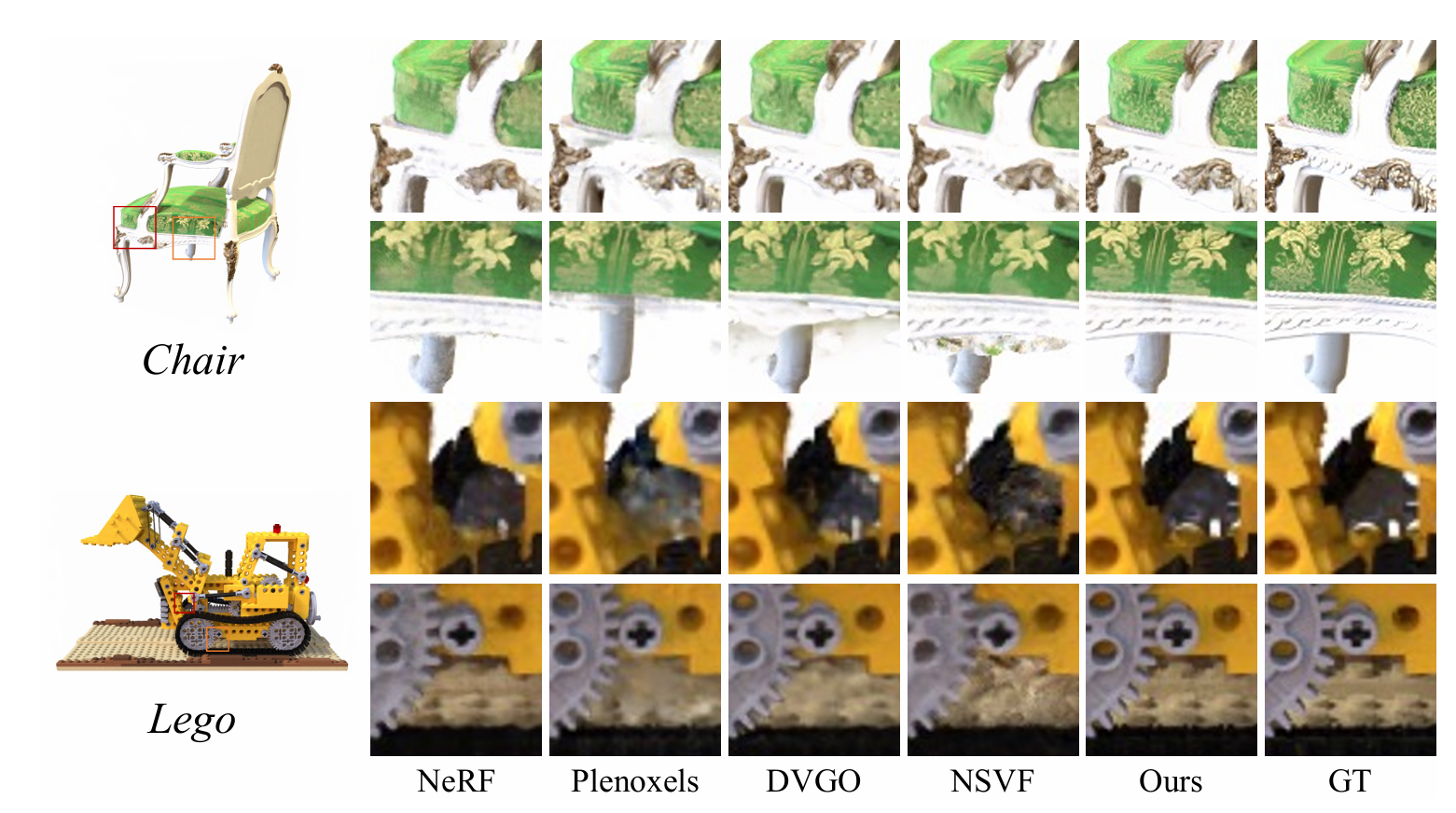
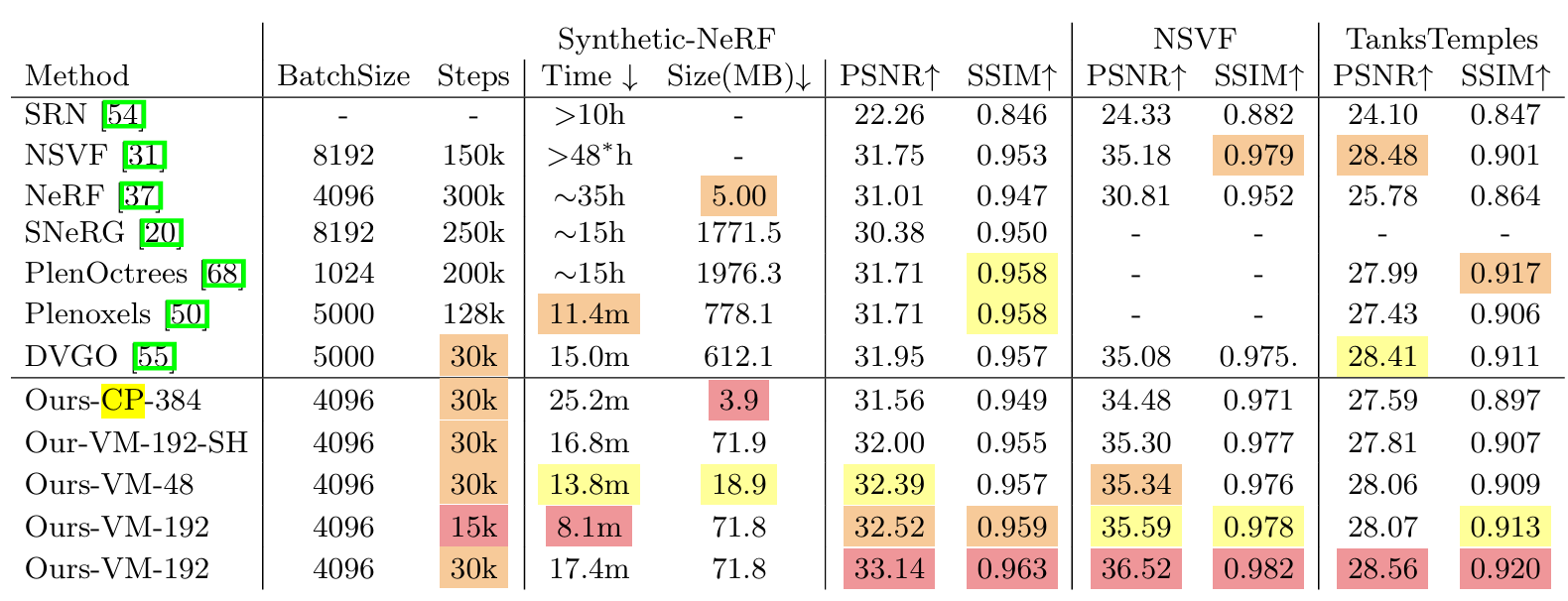
在性能与效率上相较已有方法有提升。

总结

本文通过外积的方式对三维的张量进行了分解为一维和二维的成分，从而降低了需要存储的表的大小。采样时则通过在一维和二维上做插值实现。

某种程度上，本文方法通过对特征表的组织方式进行优化，实现了对表的压缩，并且将大部分的参数量都放在了表中。其核心思想与InstantNGP有相近之处。

之前在网上看到评论说是否可以再加上InstantNGP的优化，但个人以为，参数量的压缩应是有极限的。一些论文的结果显示，INR的压缩比并不能极大突破现有有损压缩算法的极限，也就证明了其存在某种压缩性能上的极限或者是边际效应。多种相近优化方法的堆叠可能难以发挥出可观的效果。

当然，也期待研究者提出更加高效的算法。