Acorn: Adaptive Coordinate Networks for Neural Scene Representation

Acorn: Adaptive Coordinate Networks for Neural Scene Representation

Acorn：通过分块优化INR的效率
代码仓库

动机

信号存在大量冗余，因此需要根据内容动态分配区域，即对于细节更丰富的区域分配更多的块。

方法

算法流程

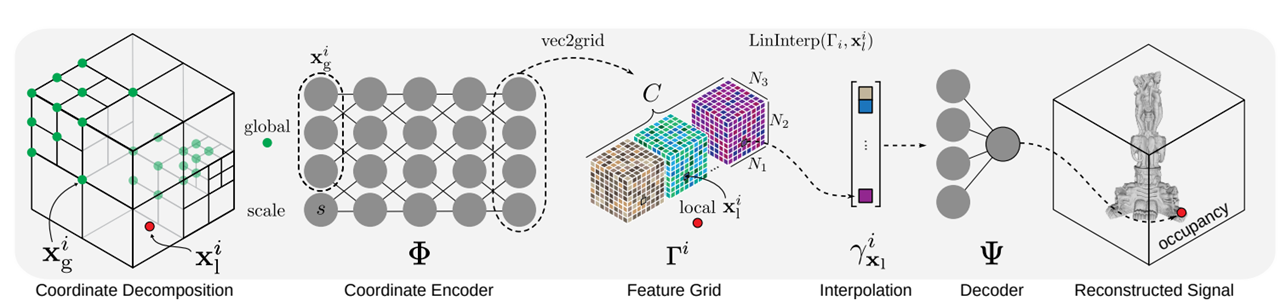
1. 分块
2. 将块坐标（全局坐标）映射为特征网格（Feature Grid）。
3. 根据点在块的内部坐标（局部坐标）从特征网格中插值获得特征。

优化分块

整数规划

假设已经有一个分块的决策，对于每个块，有三种动作：融合、不变、细分：

\[\mathbf{I}_i=(I^{\uparrow}_i,I^{=}_i,I^{\downarrow}_i)^T\in\{0,1\}^3 \]

一个区域是否融合，取决于其所有兄弟块\(\mathbf{S}(i)\)的融合标记是否为1：

\[I^g_i\overset{\mathrm{def.}}{=} \frac{1}{N_S}(I^{\uparrow}_i + \sum_{j\in\mathcal{S}(i)}I^{\uparrow}_j) \]

每个块定义一组权重：

\[\mathbf{w}_i=(w^{\uparrow}_i,w^{=}_i,w^{\downarrow}_i)^T \]

优化目标为最小化\(\sum_i{\mathbf{w}_i^T\mathbf{I}_i}\)

限制条件为三种决策互斥且总数有限：

\[I^{\uparrow}_i+I^{=}_i+I^{\downarrow}_i=1 \]

\[(\sum_i\frac{1}{N_S}I^{\uparrow}_i+I^{=}_i+N_SI^{\downarrow}_i) \leq N_B \]

其中，\(N_S\)表示执行细分操作时一个块的子块个数；\(N_B\)表示最大总块数。

块权重计算

权重的计算根据网络回归的误差\(E^i\)计算。\(w^{=}_i\)直接按照体积/面积计算\(w^{=}_i=\mathrm{Vol}_i\cdot E^i\)

\(w^{\uparrow}_i\)则考虑父节点\(\mathcal{P}(i)\)的权重\(w^{=}_{\mathcal{P}(i)}\)：

\[w^{\uparrow}_i = \left \{ \begin{array}{ll} \frac{1}{N_S}w^{=}_{\mathcal{P}(i)} & \text{如果父节点的误差可用} \\ (N_S+\alpha)w^{=}_i & \text{其他} \end{array} \right . \]

其中，若设置\(\alpha>0\)则相当于假设块融合的误差大于\(N_S\)倍的\(w^{=}_i\)。

类似的，\(w^{\uparrow}_i\)则考虑子节点\(\mathcal{C}(i)\)的权重：

\[w^{\uparrow}_i = \left \{ \begin{array}{ll} \sum_{j=\mathcal{C}(i)} w^{=}_{j} & \text{如果子节点的误差可用} \\ (\frac{1}{N_S}-\beta)w^{=}_i & \text{其他} \end{array} \right . \]

其中，若设置\(\beta>0\)则相当于假设块融合的误差小于\(\frac{1}{N_S}\)倍的\(w^{=}_i\)。

训练流程

剪枝

存在一些区域的内容是非常一致的，例如空白、单色。为了减少在这些情况下的操作，这些区域不再考虑在块划分中，即不可细分并在一个表中储存其值。参照对块总数的限制条件，这些被固定的块相当于释放了更多的细分空间给其他块，从而导致更好的划分结果。实际实践中，根据以下原则判断是否剪枝：

• 低回归误差
• 低块内方差

实验

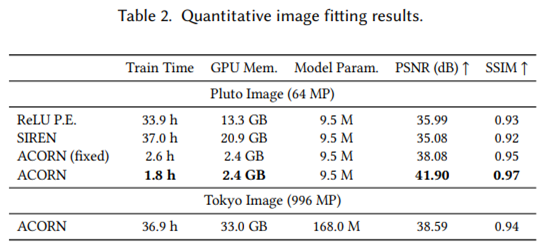
能够显著降低训练时间，同时也能提升回归精度。

总结

通过分块来实现动态的参数量分配，这也是常见的一种优化方式。本文通过在训练过程中执行整数规划动态调整块的划分，即决定需要参与训练的全局坐标集合。这一过程相当于是在调整每一轮训练过程中的坐标采样策略。

由于本人并没有复现过本文工作，所以发散出了一个担忧：在网络输出波动比较大的情况下，每轮的划分情况也可能会剧烈变化，那么是否也会因此导致网络收敛难度变大，又再次导致每轮网络输出变化较大？当然，理想情况下，网络能在多轮训练后逐渐减小拟合误差，也能够保证训练过程顺利进行。但依然比较担忧前期的一些训练是否需要大量工程经验进行调优。