Manacher OvO'
Manacher
注:全文字符串下标自 \(1\) 开始
呃......
众所周知, 在 \(NOI2025\) 大纲中这个玩意已经属于提高组了
对于任何字符串不会的我真的是太可怕了, 所以连夜补习终于学会马拉车
做个小整理, 不知道为什么觉得今年刚加进来说不定会考......
What is Manacher?
Manacher是一个用来求解字符串中每个位置的最长回文半径的算法
它的时间复杂度也很优秀, 是可爱的 \(O(n)\)
而且代码实现极其简单, 水题时很爽.
先给一下原理, 随便讲讲
How Can I Do My Manacher
奇偶化一
我们发现回文子串有一个很恶心的点: 它的长度有的是奇数, 有的是偶数
其它问题还好说, 但现在我们要干的是求长度, 每次考虑中间会让我说出及其恶毒的语言
所以我们使用一个操作: 将每个字符之间插入一个奇怪的字符(不是原字符串中出现的)
举个例子
原串: ABCBABA
我们转化成: #-A-B-C-B-A-B-A-
为什么要最左边的奇怪字符呢?
呃......我们后边需要对回文半径进行暴力扩展, 放一个防止越界
如此一来, 我们便将所有的子串转化成奇数
怎么个事
我们先设回文半径为 \(d[i]\) 方便我们表示
如果我们一个一个去暴力求解, 我们会得到 \(O(n^2)\) , 没错你的好朋友 \(O(n^2)\)
这个复杂度让 \(CCF\) 看了都流泪, 连夜整出一堆很水的数据让你通过
我们可以类比其他字符串算法的思想
现在我们已经求出来了 \([1,i-1]\) 内所有的 \(d\)
我们寻找有无办法迅速推出现在的 \(d[i]\)
类比扩展KMP(这个都会吧...不会也没有关系), 我们可以整一个加速的盒子
"盒子"是什么?
在Manacher中, 我们需要维护一个最长的回文子串, 这样在推下一个位置的时候我们可以通过回文子串的性质强硬使用对称减少无用的扩展
具体如下图
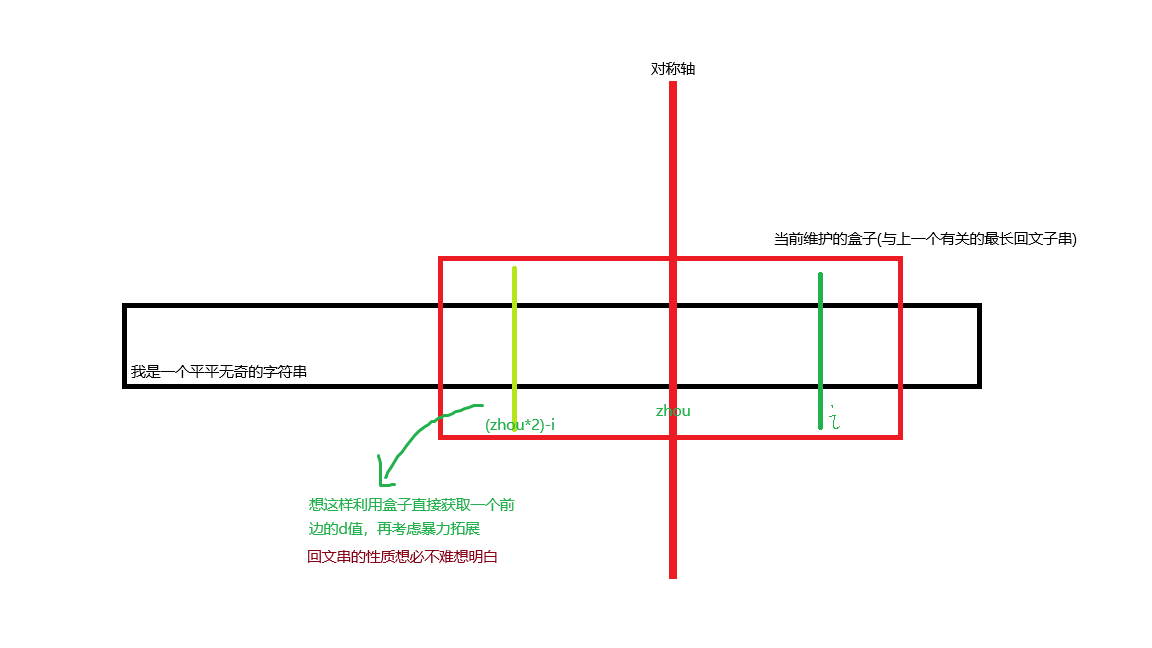
我们直接继承 \(d[i]\) 为 \(min(d[(zhou*2)-i], r-i+1)\)
\(r\) 所代表的是盒子的右端点, 取最小值保证在盒子内
之后我们一直暴力扩展, 如果 \(s[i+d[i]]=s[i-d[i]]\) , 我们就直接将 \(d[i]\) 加一, 直到无法暴力扩展
最后我们再进行判断这个盒子可不可以暴力拓展
具体来说:
判断一下 \(i+d[i]-1>=r\) 吗?
如果大于, 我们便将 \(r\) 设为 \(i+d[i]-1\)
将轴设为 \(i\)
这样就结束了(本人喜欢在代码中把判断写成\(i+d[i]>r\))
Why \(O(n)\) ?
有人会问: 都暴力扩展了辣么多次, 你凭什么说这个是线性的? 我不信.
这个的解释跟扩展KMP也特别像(凭啥要叫扩展KMP啊喂)
这个其实很好想, 我们每次暴力扩展中都会增加 \(r\), 而这个 \(r\) 是只升不降的, 在 \(r\) 内的我们又可以直接推得
所以我们暴力扩展其实是 \(O(n)\) 的.
就这么简单, 没想到吧
给一下代码:
模板: Manacher 模板
#include <bits/stdc++.h>
using namespace std;
const int MN=3e7+317;
char s[MN];
int ans=0, d[MN], length=1;
void Read(){
char r=getchar(); s[0]='$'; s[length]='-';
while(r>='a'&&r<='z'){
s[++length]=r;
s[++length]='-';
r=getchar();
}
s[length]='-';
}
void Manacher(){
for(int i=1,j=0,zhou=0; i<=length; ++i){
d[i]=min(d[(zhou<<1)-i],j-i+1);
while(s[i+d[i]]==s[i-d[i]]) d[i]++;
if(i+d[i]>j){
j=i+d[i]-1;
zhou=i;
}
ans=max(ans,d[i]);
}
}
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
Read(); Manacher(); cout<<ans-1<<'\n';
return 0;
}
和 \(wyx\) 一样短小精悍
有趣的题目
随便给一些
国集:拉拉队排练
题意简述
给定一个长度为
n的小写字母字符串,统计所有长度为奇数的回文子串。
将这些回文子串按长度降序排序,取前K个长度的乘积(模19930726)。若总数不足K个,输出-1。
就直接去跑 \(Manacher\), 跑完了把非插入符的回文半径存一下(这个就是字串长度,有插入符)
#include
#define int long long
using namespace std;
const int MN=2e6+316;
const int mod=19930726;
int n, k, d[MN], length=1;
int cnt[MN], sum=0, ans=1;
string str; char s[MN];
void Read(){
s[0]='%', s[length]='-';
for(auto c:str){
s[++length]=c;
s[++length]='-';
}
s[length]='-';
}
void Manacher(){
for(int i=1,j=0,zhou=0; i<=length; ++i){
d[i]=min(d[(zhou<<1)-i],j-i+1);
while(s[i+d[i]]==s[i-d[i]]) d[i]++;
if(i+d[i]>j){
j=i+d[i]-1;
zhou=i;
}
if((d[i]-1)%2) cnt[d[i]-1]++;
}
}
int quick_power(int a, int b){
int res=1;
while(b){
if(b&1){
res=(res*a)%mod;
}
a=(a*a)%mod;
b>>=1;
}
return res;
}
signed main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>n>>k>>str; Read(); Manacher(); n=length;
for(int i=n; i>=1; --i){
if(i%2==0) continue;
sum+=cnt[i];
int use=min(k, sum);
ans=(ans * quick_power(i, use)) % mod;
k-=use;
if(k<=0) break;
}
if(k>0) ans=-1;
cout<<ans<<'\n';
return 0;
}
这个就没啦
绿绿和串串
题意简述
给定字符串 \(S\),求所有可能的初始串 \(R\) 的长度(\(|R| \leq |S|\)),使得 \(R\) 经过若干次翻转操作后得到的串以 \(S\) 为前缀。
翻转操作定义:每次操作将前 \(|R|-1\) 个字符倒序拼接到 \(R\) 末尾(例如
abcd→abcdcba)。
数据范围:\(|S| \leq 10^6\),总 \(\sum |S| \leq 5 \times 10^6\)。
我们要多动手, 手摸一下?
发现想要能换过去必须满足以下任意条件:
- 本身的最长回文字串可以到整个右边的边界
- 本身的最长回文字串可以碰到上一条可以的回文中心
这个自己画图想想就懂了
代码↓
#include <bits/stdc++.h>
using namespace std;
const int MN=5e6+516;
string rs; char s[MN];
int d[MN], length=1, can[MN], ans=0;
void Read(){
s[0]='$', s[length]='-';
for(auto c:rs){
s[++length]=c;
s[++length]='-';
}
s[length]='-';
}
void Manacher(){
for(int i=1,j=0,zhou=0; i<=length; ++i){
d[i]=min(d[(zhou<<1)-i],j-i+1);
while(s[i+d[i]]==s[i-d[i]]) d[i]++;
if(i+d[i]>j){
j=i+d[i]-1;
zhou=i;
}
}
}
void init(){
memset(s,0,sizeof(s));
memset(can,0,sizeof(can)); ans=0;
memset(d,0,sizeof(d)); length=1;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int T; cin>>T;
while(T--){
init(); cin>>rs; Read(); Manacher();
for(int i=length; i>=1; --i){
if(s[i]=='-') continue;
if (i+d[i]-1==length) can[i]=1;
else if(can[i+d[i]-2]&&i==d[i]) can[i]=1;
}
for(int i=1; i<=length; ++i) if(can[i]) cout<<(i/2)<<" ";
cout<<'\n';
}
return 0;
}
最后一道
CF17E Palisection
给定一个长度为 n 的小写字母串 S,求有多少对相交的回文子串(包含也算相交)。
注意是多少对
这个咋整? 看到相交, 还有回文子串, 我们会往回文子串上边去想
我们如果知道了回文半径, 那么去计算不相交很简单
那么就把所有的减去不相交的
具体如何去算?
\(f[i]\) 表示以 \(i\) 开头的回文串有几个
\(g[i]\) 表示以 \(i\) 结尾的回文串有几个
\(sum[i]\) 是 \(g[i]\) 的前缀和
一个位置的贡献是 \(sum[i]*f[i+1]\)
就是前边所有可以被拎出来的和当前位置的搞一个乘法原理
这样我们把所有的加起来就行
\(f[i],g[i]\) 我们用 线段树或者树状数组 差分来求.
跑完一次 \(Manacher\) 之后, 我们对于每一个点搞差分, 作如下操作
f[i-d[i]+1]++;
f[i+1]--;
g[i]++;
g[i+d[i]]--;
很好理解, 一个位置对于 \(f[i]\) 的贡献是 \([i-d[i]+1,i]\) 的
同理对于 \(g[i]\) 的贡献是 \([i,i+d[i]-1]\) 的
就这样搞, 最后一加, 直接统计
代码↓
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MN=5e6+516;
const int mod=51123987;
int n, ans, sum, tot, f[MN], g[MN], d[MN];
char s[MN]; string sc;
int length=1;
void Manacher(){
s[0]='*'; s[length]='-';
for(auto c:sc){
s[++length]=c;
s[++length]='-';
}
s[length]='-';
for(int i=1,j=0,zhou=0; i<=length; ++i){
d[i]=min(d[(zhou<<1)-i],j-i+1);
while(s[i+d[i]]==s[i-d[i]]) ++d[i];
if(i+d[i]>j){
j=i+d[i]-1;
zhou=i;
}
tot=(tot+(d[i]>>1)%mod)%mod;
}
}
signed main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin>>n>>sc; Manacher();
for(int i=1; i<=length; ++i){
f[i-d[i]+1]++; f[i+1]--;
g[i]++; g[i+d[i]]--;
}
for(int i=1; i<=length; ++i){
f[i]+=f[i-1]; g[i]+=g[i-1];
}
ans=tot*(tot-1)/2%mod;
for(int i=2; i<=length-2; i+=2){
sum=(sum+g[i])%mod;
ans=(ans-sum*f[i+2]%mod+mod)%mod;
}
cout<<ans<<'\n';
return 0;
}
/*
- 1
b 2
- 1
a 4
- 1
b 2
- 3
b 2
- 1
*/
就这样, 喵


 浙公网安备 33010602011771号
浙公网安备 33010602011771号