ReTF 模拟赛的一道题
原题用下面的做法可以强制在线,\(1\log\) 时空
upd:\(1\log\) 是假的,还是 \(2\log\)
没注意到支配对也是可以做的。
考虑如何求区间 mex,线段树扫描 \(r\),维护 \(lst_i\) 代表 \(i\) 最后一次出现的位置,只需要线段树二分即可。在线就把扫描线变成主席树。
回到这个题,注意到只需要关心所有长度为 \(k\) 的区间,为了方便将 \(lst_i\) 的定义改成到 \(r\) 的距离。本质上就是,对于扫描线在 \([l+k-1,r]\) 处的所有线段树查询信息。二分 mex 为 \(x+1\),需要求出是否存在一棵 \([l+k-1,r]\) 中的线段树满足 \([0,x]\) 上的权值 \(<k\),画到二维平面上长这个样子:
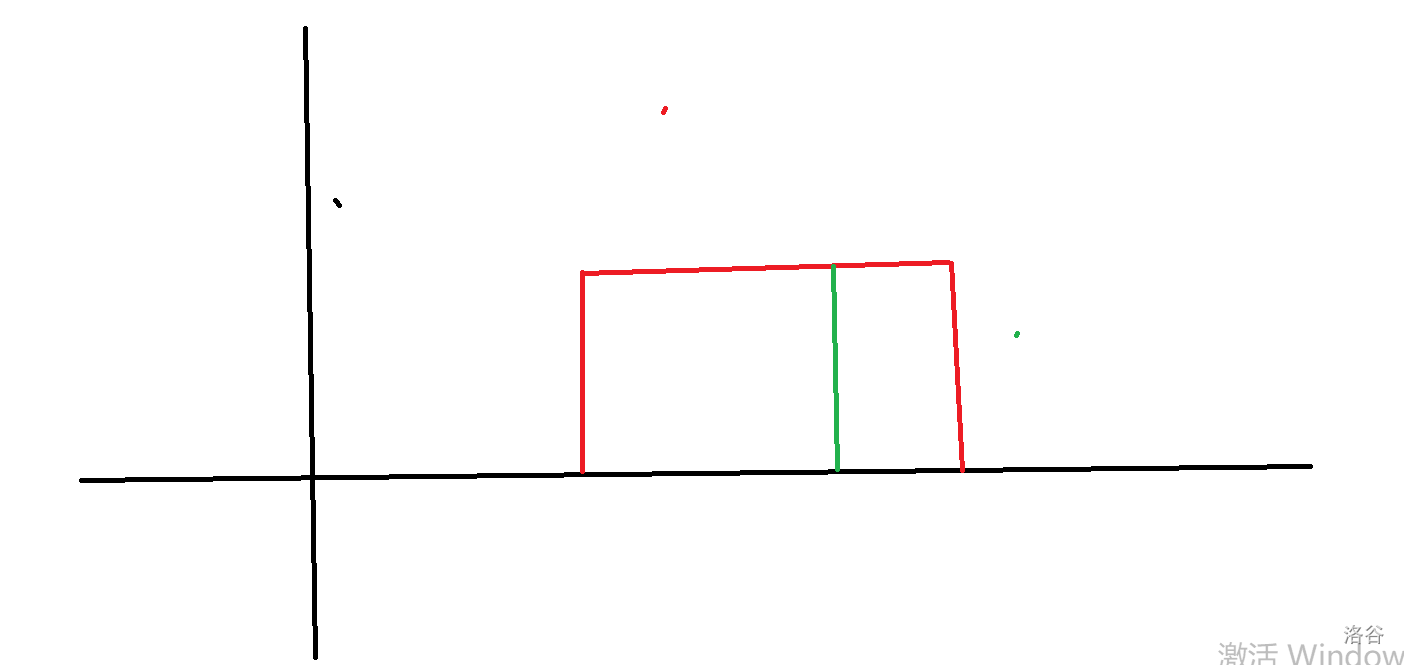
即需要判断红色矩形内是否存在那样一条绿线满足线上的值全部 \(<k\),先整体二分一下。注意到矩形是 3-side 的,横轴有两维限制,纵轴只有一维。于是换维扫描线,此时线段树维护扫到某个纵坐标时,所有横坐标的历史最大值。实际上是:
-
修改,对于一段区间 \([l,r]\),依次将 \(v_l\sim v_r\) 对 \(0,1,2,\dots,r-l+1\) check max。
-
询问,查询区间最小值。
可以发现修改次数是和 \(n\) 线性相关。注意到修改之间实际上有支配关系,我们可以将修改操作变成区间赋值成 \(x,x+1,\dots\)。这样加上整体二分就是 \(2\log\) 的。
场上止步于此了。可以发现将整体二分变成主席树就是 \(1\log\) 了,这一步没发现有点菜。
修改操作的支配关系:注意到对于一个位置 \(x\),只需要关注包含它的最远一个修改。那么对于修改 \((l,r)\),找到 \(m\) 为前面操作中修改左端点 \(\in[1,l]\),右端点的最大值。那么只需对 \([m+1,r]\) 做区间赋值即可。
2log 的代码:
#pragma GCC optimize(3)
#include<bits/stdc++.h>
//#define int long long
#define fi first
#define se second
#define pii std::pair<int,int>
#define vint std::vector<int>
#define vpair std::vector<pii>
#define all(x) (x).begin(),(x).end()
#define SZ(x) (x).size()
#define debug(...) fprintf(stderr,##__VA_ARGS__)
template<typename T>
void read(T &x){
x=0;
int f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9') x=x*10+(int)(c-'0'),c=getchar();
x*=f;
}
std::stack<char>st;
template<typename T>
void print(T x){
if(x==0) putchar('0');
if(x<0) putchar('-'),x=-x;
while(st.size()) st.pop();
while(x) st.push((char)('0'+x%10)),x/=10;
while(st.size()) putchar(st.top()),st.pop();
}
template<typename T>
void printsp(T x){
print(x),putchar(' ');
}
template<typename T>
void println(T x){
print(x),putchar('\n');
}
template<typename T,typename I>
bool chkmin(T &a,I b){
if(a>b) return a=b,1;
return 0;
}
template<typename T,typename I>
bool chkmax(T &a,I b){
if(a<b) return a=b,1;
return 0;
}
template<typename T,typename I>
void addedge(std::vector<I>*vec,T u,T v){
vec[u].push_back(v);
}
template<typename T,typename I,typename K>
void addedge(std::vector<K>*vec,T u,T v,I w){
vec[u].push_back({v,w});
}
template<typename T,typename I>
void addd(std::vector<I>*vec,T u,T v){
addedge(vec,u,v),addedge(vec,v,u);
}
template<typename T,typename I,typename K>
void addd(std::vector<K>*vec,T u,T v,I w){
addedge(vec,u,v,w),addedge(vec,v,u,w);
}
bool Mbe;
const int inf=1e9,MOD1=998244353,MOD2=1e9+7;
const int maxn=1e6+10;
int n,q,a[maxn],ans[maxn];
vint pos[maxn];
struct info{
int l,r,k,id,ml,mr,mid;
}b[maxn];
struct segtree{
int l[maxn*2],r[maxn*2],ls[maxn*2],rs[maxn*2],lz[maxn*2],mi[maxn*2],tot;
void clear(){
tot=0;
}
void dfs(int p){
if(!p) return ;
mi[p]=inf,lz[p]=-1;
dfs(ls[p]),dfs(rs[p]);
}
void push_up(int p){
mi[p]=std::min(mi[ls[p]],mi[rs[p]]);
}
int build(int L,int R){
int p=++tot;
l[p]=L,r[p]=R,lz[p]=-1;
if(L==R) return mi[p]=inf,p;
int mid=(L+R)>>1;
ls[p]=build(L,mid),rs[p]=build(mid+1,R);
return push_up(p),p;
}
void push_down(int p){
if(lz[p]==-1) return ;
mi[ls[p]]=lz[ls[p]]=lz[p],mi[rs[p]]=lz[rs[p]]=lz[p]+r[ls[p]]-l[ls[p]]+1;
lz[p]=-1;
}
void update(int p,int L,int R,int x){
if(l[p]>=L&&r[p]<=R){
x=x+l[p]-L;
lz[p]=mi[p]=x;
return ;
}
push_down(p);
int mid=(l[p]+r[p])>>1;
if(mid>=L) update(ls[p],L,R,x);
if(R>mid) update(rs[p],L,R,x);
return push_up(p),void();
}
int query(int p,int L,int R){
if(L>R) return inf;
if(l[p]>=L&&r[p]<=R) return mi[p];
push_down(p);
int mid=(l[p]+r[p])>>1,res=inf;
if(mid>=L) chkmin(res,query(ls[p],L,R));
if(R>mid) chkmin(res,query(rs[p],L,R));
return res;
}
}ds;
struct BIT{
int mx[maxn];
void clear(){
for(int i=1;i<=n;i++) mx[i]=0;
}
int lowbit(int x){
return x&(-x);
}
void upd(int p,int x){
for(;p<=n;p+=lowbit(p)) chkmax(mx[p],x);
}
int qry(int p){
int res=-1;
while(p) chkmax(res,mx[p]),p-=lowbit(p);
return res;
}
}ds_;
bool cmp(info x,info y){
return x.mid<y.mid;
}
void upd(int l,int r,int y){
int x=ds_.qry(l);
chkmax(x,l-1);
if(x>=r) return ;
ds.update(1,x+1,r,x-l+1+y);
ds_.upd(l,r);
}
void solve(){
for(int i=1;i<=q;i++){
if(b[i].ml>b[i].mr) b[i].mid=inf;
else b[i].mid=(b[i].ml+b[i].mr)>>1;
}
std::sort(b+1,b+q+1,cmp);
int z=1,m=0;
ds.clear(),ds.dfs(1),ds_.clear();
for(int i=0;i<n;i++){
if(pos[i].size()){
int las=pos[i][0];
chkmax(m,las-1);
for(int j=1;j<pos[i].size();j++){
if(pos[i][j]-1>m) upd(las,pos[i][j]-1,0);
las=pos[i][j];
}
upd(las,n,0);
}else m=n;
while(z<=q&&b[z].mid==i){
if(ds.query(1,std::max(b[z].l,m+1),b[z].r)<b[z].k) b[z].ml=b[z].mid+1;
else b[z].mr=b[z].mid-1;
z++;
}
if(z>q||b[z].mid==inf) break;
}
}
bool Men;
signed main(){
freopen("vmefifty.in","r",stdin),freopen("vmefifty.out","w",stdout);
debug("%.6lfMB\n",(&Mbe-&Men)/1048576.0);
read(n),read(q);
for(int i=1;i<=n;i++){
read(a[i]);
if(a[i]<n) pos[a[i]].push_back(i);
}
for(int i=1;i<=q;i++){
read(b[i].l),read(b[i].r),read(b[i].k);
b[i].ml=0,b[i].mr=n-1,b[i].id=i;
if(b[i].k>b[i].r-b[i].l+1) b[i].k=b[i].r-b[i].l+1;
b[i].l+=b[i].k-1;
}
ds.build(1,n);
while(1){
bool fl=0;
for(int i=1;i<=q;i++){
if(b[i].ml<=b[i].mr){
solve();
fl=1;
break;
}
}
if(!fl) break;
}
for(int i=1;i<=q;i++) ans[b[i].id]=b[i].ml;
for(int i=1;i<=q;i++) println(ans[i]);
debug("%.6lfms\n",1e3*clock()/CLOCKS_PER_SEC);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号