三轮省集

一类分治问题

实际上是 P7723 的题解，不过只提取了关键的思想。

算是一个 trick？

类似 gxy001 的题解，先考虑这个问题：

给出平面上的 \(n\) 个点，\(m\) 条线，每条线的某一侧会有修改/查询。

这 \(m\) 条线将整个平面分成了 \(f(m)\) 个等价类，每个等价类内部得到的修改/查询是一致的。显然一个等价类会被多次修改/查询，我们之前遇到的等价类被多次修改一般是如下情景：

维护序列，区间修改/查询。

这是非常模板的线段树维护信息，考虑线段树究竟在干什么。我们维护的信息是序列上的点，每个点都是一个等价类，每次修改总是将一段连续的等价类修改，因此我们将一些连续的等价类合并，由于修改存在结合律，可以利用标记来代表连续等价类的信息。

上文中我们在利用一种树形结构，满足每个节点维护的都是若干个等价类，其中父亲的等价类是儿子等价类的并，在将一个大等价类拆成两个小等价类时完成信息的下放。

回到 gxy001 所提到的那个问题。这个问题中我们无法找到一种良好的等价类合并方式使得整个复杂度是对的，同时鉴于等价类数量和操作次数息息相关，考虑将上面的过程反过来。

换句话说，我们依然利用一种树形结构，满足每个节点维护的都是若干等价类，但是儿子等价类是父亲等价类做一些合并后得到的。将所有操作按照时间分治，此时儿子的等价类数量为 \(f(\frac m2)\)（线的数量减半了）。那么我们修改的时候只需在儿子上打标记，等到从儿子到父亲这一需要拆开等价类集合的过程中传递标记即可。

如何将这个东西应用到题目上？

---

一类 dp 问题

考虑一个凸包（不妨设上凸包），用斜率为 \(p\) 的直线去切它，切到的点必然满足 \(f(x)-xp\) 最大。因为考虑切到的样子：

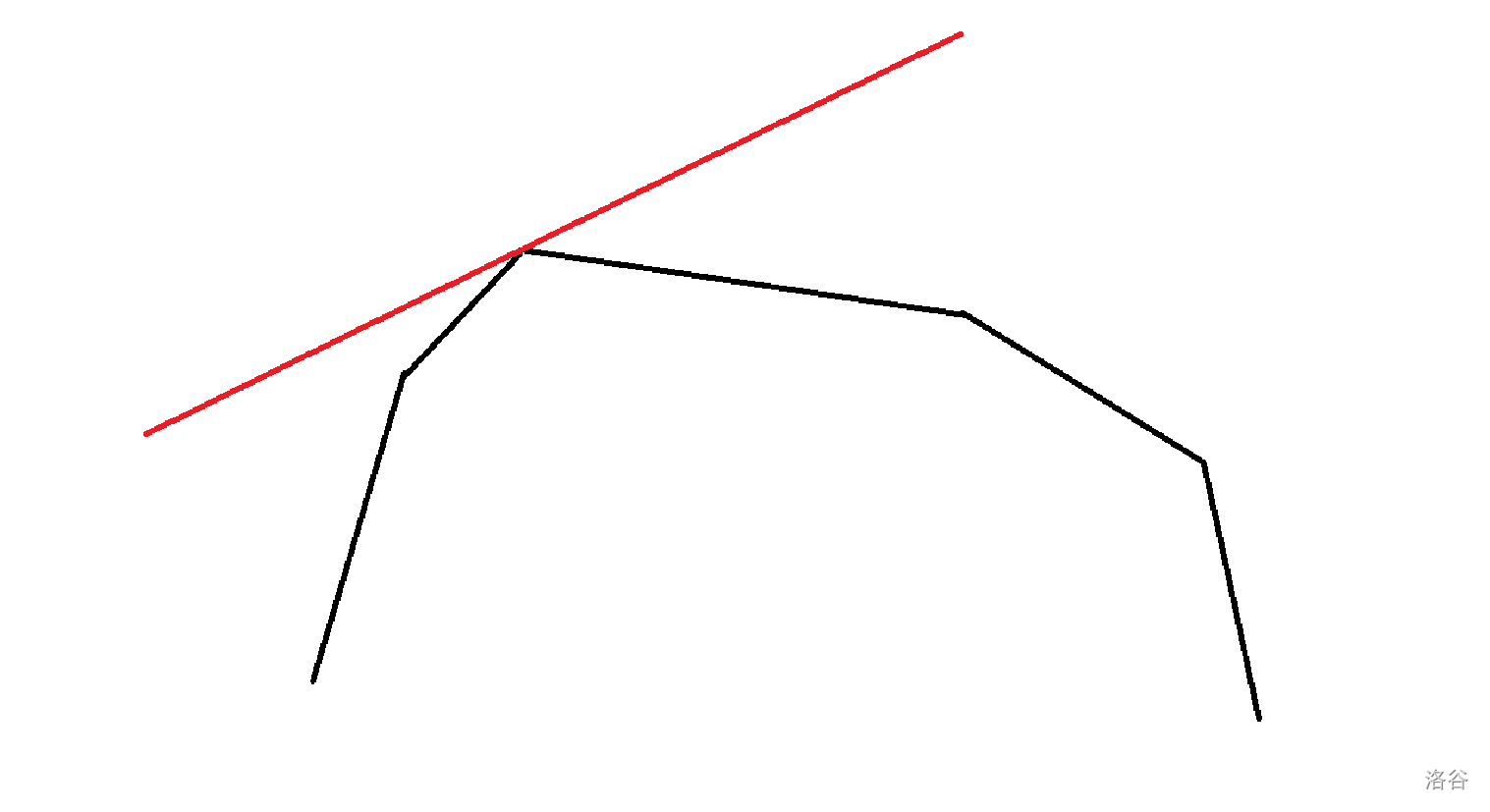
此时的直线可能是 \(px+b\)，显然切到的点满足 \(f(x)-(px+b)\) 最大，即 \(f(x)-(xp+b)>f(x')-(x'p+b)\to f(x)-xp>f(x')-x'p\)。

二分斜率 \(p\)，此时切到的点随 \(p\) 的增大逐渐左移，判断切到的点是哪个只需求出最小的 \(f(x)-xp\) 和对应的 \(x\) 即可。

---

定义两个点集的闵可夫斯基和为点集的笛卡尔积。两个凸包的闵可夫斯基和满足旧凸包的每一条边都在新凸包出现恰好一次，因此将两个凸包原先的边按照斜率排序后即可得到新凸包。

考虑两个数组 \(f\) 和 \(g\)，按照 \((i,f_i)\) 的形式放到平面上，假设两个数组都是下凸的。考虑其 \((\min,+)\) 卷积：

\[h_i=\min\limits_{j+k=i}(f_j+g_k) \]

观察到等价于两个数组做闵可夫斯基和后在 \(i\) 处的最低点，即做闵可夫斯基和后的下凸壳。由于按照斜率就是 \(f_i-f_{i-1}\)，且斜率单调，做归并后就能得到闵可夫斯基和的结果。

---

记一个验证凸性的方法：

满足四边形不等式的矩阵称为蒙日矩阵，蒙日矩阵 \((\max,+)\) 卷积的 \(k\) 次幂中每个位置都关于 \(k\) 凸。Itst 的博客指出，满足四边形不等式的序列划分类问题关于划分段数总是凸的。

---

zhenjianuo2025 非常会的东西！

lxl 课上讲了，但是没听。dx 的论文比 lxl 的课件对一点！

问题 \(B\) 强于问题 \(A\) 意味着 \(B\) 无法在低于 \(A\) 的复杂度内解决。

若调用较少次 \(B\) 问题就能解决 \(A\) 问题，则 \(B\) 强于 \(A\)。意味着对于当前 \(A\) 的最优时间复杂度 \(f(A)\)，有 \(B\) 的最优时间复杂度 \(f(B)\) 不低于 \(f(A)\)。

“较少次”定义为代价不超过求解问题 \(B\) 的时间复杂度。这也意味着在 OI 中，有 \(f(B)\ge f(A)^{0.5}\)。

以下不考虑均摊。

整矩阵乘法到 01 矩阵乘法的归约

需要调用多少次 \(01\) 矩阵乘法才能解决整数矩阵乘法？

令 \(a=\sum 2^ia_i\)，则 \(ab=\sum 2^{i+j}a_ib_j\)，因此调用 \(\log^2 V\) 次 \(01\) 矩阵乘法就可以解决整数矩阵乘法，由于整数矩阵乘法的复杂度不能低于 \(O(n^{\omega})\)，因此 \(01\) 矩阵乘法也是无法低于该复杂度。

01 矩阵乘法强于整数矩阵乘法。

bool 矩阵乘法到 01 矩阵乘法的归约

需要调用多少次 01 矩阵乘法能解决 bool 矩阵乘法。

只需做一次 01 矩阵乘法就能得到 bool 矩阵乘法的结果，因此 01 矩阵乘法强于 bool 矩阵乘法。

构造信息集合交

\(n\) 个集合 \(S\) 和 \(m\) 个集合 \(T\)，每个集合都是 \(\{1,2,\dots,k\}\) 的子集，求 \(|S_i\cup T_j|\)。

调用多少次上述问题的求解能解决 01 矩阵乘法？

令 \(A_{i,j}=[j\in S_i]\)，\(B_{i,j}=[i\in T_j]\)，则 \((A\times B)_{i,j}=|S_i\cup T_j|\)。我们只需调用一次上述问题的求解就能解决 \(01\) 矩阵乘法。因此上述问题强于 \(01\) 矩阵乘法。

将该问题称作 信息集合交 问题。

链颜色数到矩阵乘法的归约

定义 链颜色数 问题为：给出树上每个点的颜色，查询一条链上的颜色数。点数 \(n\)，询问次数 \(q\)。

调用多少次 链颜色数 问题的求解能解决 信息集合交 问题？

不必拘泥于树的形态需要一般。将树的形态设置为菊花套链，引出 \(n'+m'\) 条链代表 信息集合交 问题中的 \(S_i\) 和 \(T_j\)，其中 \(k=\sqrt{n}\)。则询问 \(n'm'\) 次即可回答 \(\sqrt n\) 规模的 信息集合交 问题。

因此 链颜色数 问题强于信息集合交问题，复杂度下界为 \(O(n^{\frac\omega2})\)。

区间逆序对到 01 矩阵矩乘的归约

定义区间逆序对问题为给出长为 \(n\) 的序列 \(a\)，\(q\) 次询问 \(l,r\)，求出 \(\sum\limits_{l\le i<j\le r}[a_i>a_j]\)。

调用多少次 区间逆序对 问题能解决 01 矩乘 问题？

感谢 zhenjianuo2025。

考虑两个 \(\sqrt{\frac n2}\) 级别的 01 矩阵相乘，两个对应位置无非四种情况：00，01，10，11。我们将第一个矩阵 \(A\) 按照行摊平，将第二个矩阵 \(B\) 按照列摊平并接在 \(A\) 摊平的结果后面。权值按照如下方式：

• 对于矩阵 \(A\)，若 \(A_{i,j}=0\) 则权值为 \(\infty\)，否则为 \(\sqrt{\frac n2}+i\)。

• 对于矩阵 \(B\)，若 \(B_{i,j}=0\) 则权值为 \(\infty\)，否则为 \(j\)。

考虑 \(C_{i,j}\) 的值，等价于 \(A\) 第 \(i\) 行摊开后对 \(B\) 第 \(j\) 列摊开后的逆序对数量减去 \(A_{i,k}=0\) 且 \(B_{k,j}\neq0\) 的数量。前者实际上就是区间对区间的逆序对，设两个区间为 \([l,r]\) 和 \([l',r']\)，满足 \(l\le r<l'\le r'\)，求出 \([l,r']\) 的逆序对数量后减去 \([l,l'-1]\) 和 \([r+1,r']\) 的逆序对数量，再加上 \([r+1,l'-1]\) 的逆序对数量即可。可以在 \(4\) 次询问内求出值。

后者考虑将 \(B\) 按照列摊开，\(A\) 按照行摊开接在后面做一样的事情，于是我们可以在 \(8\) 次内求出 \(C_{i,j}\) 的值。只需要做两次长度为 \(n\)，询问次数为 \(4n\) 的 区间逆序对 问题就能回答 \(\sqrt{\frac n2}\) 规模的 01 矩阵乘法问题。因此区间逆序对强于后者，复杂度下界为 \(O(n^{\frac{\omega}{2}})\)。