ABC340 G

link

官方题解一如既往胡说八道

引子

该部分将介绍计算几何的一些基本知识，均可在《算法竞赛》第八章计算几何部分找到。

斜率

对于一条直线，设直线上两点为 \((x,y),(x',y')\)，则我们称其斜率为 \(\frac{y'-y}{x'-x}\)。斜率可以刻画一条直线的倾斜程度，越靠近 \(y\) 轴的直线倾斜程度越大。

利用斜率判断线段关系

对于下图：

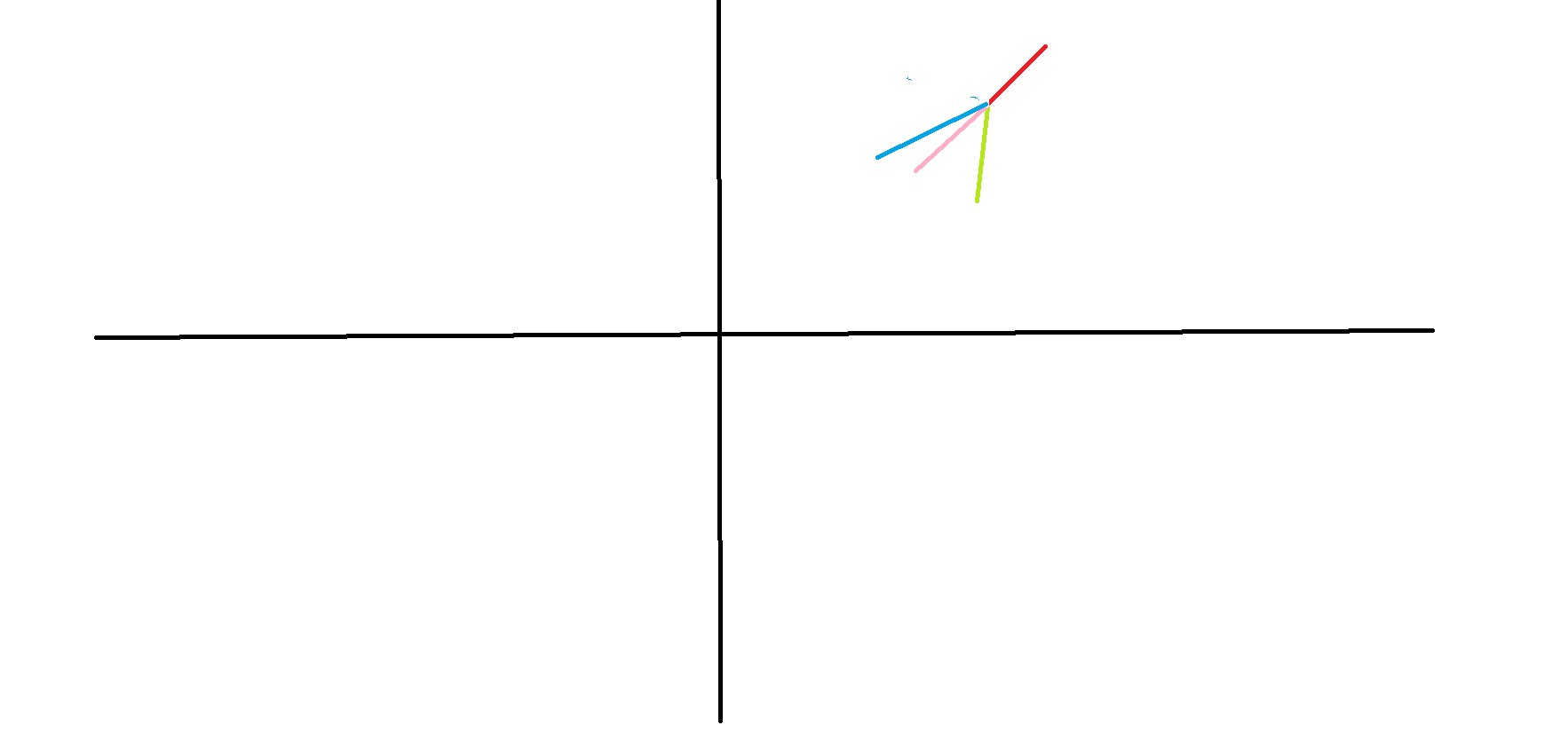
我们主要研究红色线段与其它线段夹角上的关系。

可以发现，红色线段与蓝色线段的夹角在红色线段所在直线上方。此时蓝色线段的斜率小于红色线段。

同样，红色线段与绿色线段的夹角在红色线段所在直线的下方，此时绿色线段的斜率大于红色线段。

可以证明，两者互为充要条件。

于是我们可以通过斜率之间的关系判断线段之间的关系。

凸包

对于二维平面上的若干点，凸包就是将这些点用一个凸多边形包含进来，该多边形的最小面积。可以感性理解成一个二维平面上有一个足够大的圆，这个圆不断收束，但始终要将所有点包含进去，并且要是一个凸多边形。

关于求解凸包的方法，经典的做法是利用 Graham 算法旋转找点，但复杂度为 \(O(n\log n)\)。目前主流做法是选择 Graham 的优化版本 Andrew 算法，复杂度可以做到 \(O(n)\)。

Andrew

我们将凸包的下边界称为下凸壳。

Andrew 算法分别用 \(O(n)\) 的时间复杂度求解上下凸壳，最后计算出面积。不过，在本题中我们只需要掌握求解凸壳即可。

以下凸壳为例。

将所有点按照 \(x\) 作为第一关键字，\(y\) 作为第二关键字排序后，去除重复的点。此时，\(a_1\) 一定在下凸壳上。我们利用 \(a_1\) 不断进行扩展，并记录凸壳上的点有哪些。

对于 \(a_i\)，如果从当前凸壳上最后一点向 \(a_i\) 连线可以满足凸多边形的要求，我们就将 \(a_i\) 加入凸壳中；否则将凸壳上最后一点删去，重复这一过程。如果凸壳上只剩 \(a_1\) 一点，此时将 \(a_i\) 加入凸壳即可。

如何判断是否满足凸多边形的要求？

设两条线段分别为 \((a,b)\)，\((c,d)\)，由于是下凸壳，我们必须满足 \((c,d)\) 相较于 \((a,b)\) 不能往下拐，否则会出现一个大于180°的内角，建议运用画图理解，《算法竞赛》上有着详细的说明。至于如何判断是否下拐，本质上就是判断两条线段之间的关系，运用斜率判断即可。注意在《算法竞赛》一书中采用叉积判断，略显麻烦，并且要考虑上三角函数，并不建议用这种方法。

我们求出上下凸壳后，可以利用计算几何知识计算出面积，这里不过多介绍。

ABC340 G

考虑对于 \(k\) 固定的情况下，如何求解 \(r\)。

我们不妨抽象出一个二维平面，对于每一个 \(i\)，将 \((i,A_1+A_2+\cdots +A_i)\) 作为点加进平面中。

对于 \(r\le k\)，\(\frac{A_k+A_{k+1}+\cdots +A_r}{r-k+1}\) 就是线段 \((k-1,y_1),(r,y_2)\) 的斜率，其中 \(y_1,y_2\) 分别代表对应的 \(r\)。

推导过程较为简单，考虑该线段所在直线的斜率求法为 \(\frac{y_2-y_1}{r-(k-1)}\)，根据前缀和知识，得到 \(y_2-y_1=A_k+A_{k+1}+\cdots +A_r\)，又因为 \(r-(k-1)=r-k+1\)，所以 \(\frac{A_k+A_{k+1}+\cdots +A_r}{r-k+1}=\frac{y_2-y_1}{r-(k-1)}\)。

于是我们可以理解为 \(A_k\sim A_r\) 的平均值，，等价于连接 \((k-1,y_1),(r,y_2)\) 线段所在直线的斜率。

对于固定的 \(k\)，问题可以变为在横坐标为 \(k\sim n\) 中找到一个点，使得与横坐标为 \(k-1\) 的点连接后斜率最大。

可以发现，当我们将横坐标为 \(k-1\sim n\) 的部分截取出来后，求出上凸壳，答案就是横坐标为 \(k-1\) 的点在凸壳上的下一个点。

画图极易理解，这里给出数学证明。

显然，对于一个合法的上凸壳，每一条线段所在直线的斜率都是单调不升的，因为如果存在上升，则必然会出现大于180°的内角，根据斜率与线段关系的知识可以证明，请读者自证。

我们考虑找上凸壳的过程。对于一条线段，如果满足与前面线段的斜率构成不升序列则将其加入凸壳，否则不断弹出前面线段。

根据这一过程，可以发现我们得出的结论是正确的，用反证法可以证明。

于是存在一个 \(O(n^2)\) 的做法，暴力寻找上凸壳的下一个点，显然无法通过。

我们考虑倒着求上凸壳，即从 \(A_n\) 到 \(A_1\) 来求，每次对于 \(A_i\)，记录 \(pre_i\) 代表 \(A_i\) 在上凸壳的下一个点，时间复杂度 \(O(n)\)。

注意，我们要求 \(0\sim n\) 的上凸壳。

#include<bits/stdc++.h>
#define int long long

template<typename T>
void read(T &x){
	 int f=1;
	 char c=getchar();
	 x=0;
	 while(c<'0'||c>'9'){
		 if(c=='-') f=-1;
		 c=getchar();
	 }
	 while(c>='0'&&c<='9') x=x*10+(int)(c-'0'),c=getchar();
	 x*=f;
}

template<typename T,typename I>
void chkmin(T &a,I b){
	 a=std::min(a,b);
}

template<typename T,typename I>
void chkmax(T &a,T b){
	a=std::max(a,b);
}

const int inf=1e18+10,MOD1=998244353,MOD2=1e9+7;

const int maxn=2e5+10;

const double eps=1e-6;

int a[maxn],x[maxn],y[maxn],pre[maxn],s[maxn];

signed main(){
	int n;
	read(n);
	for(int i=1;i<=n;i++) read(a[i]),x[i]=i,y[i]=y[i-1]+a[i];
	int tot=0;
	s[++tot]=n;
	for(int i=n-1;i>=0;i--){//求上凸壳 
		while(tot>1){
			int fi=s[tot-1],se=s[tot];
			double del=(y[fi]*1.0-y[se]*1.0)/(x[fi]*1.0-x[se]*1.0);
			double del2=(y[se]*1.0-y[i]*1.0)/(x[se]*1.0-x[i]*1.0);
			if(del>del2+eps) tot--;
			else break;
		}
		pre[i]=s[tot];
		s[++tot]=i;
	}
	for(int i=1;i<=n;i++){
		int p=pre[i-1];
		printf("%.8f\n",(y[p]*1.0-y[i-1]*1.0)/(x[p]*1.0-x[i-1]*1.0));//求平均数 
	}
	return 0;
}
/*
-读入字符一定检查回车
- 能不能搜索？
-函数要有返回值！
-想好了再写！
*/